Методом золотого сечения найти точку минимума функции 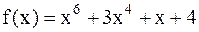 с точностью 0.1
с точностью 0.1
1. Находим отрезок локализации. При x=-1 имеем f(-1)=7, при x=0- f(0)=4, при x=1-f(1)=9. Следовательно, на отрезке [-1,1] имеется точка минимума. Полагаем a0=-1, b0=1.
2. Методом золотого сечения отрезка находим две точки:
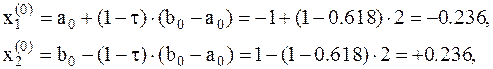
1. Вычисляем значения функции в этих точках:

2. Так как 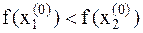 , то точка минимума находится на отрезке
, то точка минимума находится на отрезке 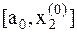 .
.
3. Имеем новый отрезок локализации
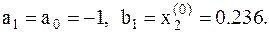
4. Определяем длину l1 отрезка [a1,b1]
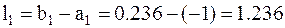 .
.
5. Так как l1=1.236>0.1, то на отрезке [a1,b1] методом золотого сечения находим две точки
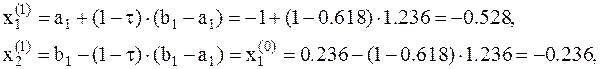 6. Вычисляем значение функции в новой точке
6. Вычисляем значение функции в новой точке 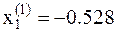 . В точке
. В точке 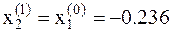 значение функции уже известно
значение функции уже известно 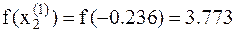 . Имеем
. Имеем
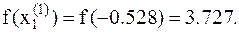
7. Так как 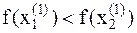 , то точка минимума находится на отрезке
, то точка минимума находится на отрезке 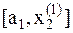 .
.
8. Имеем новый отрезок локализации
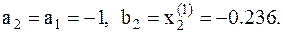
9. Определяем длину l2 отрезка [a2,b2]
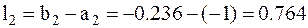 .
.
10. Так как l2>0.1, то на отрезке [a2,b2] методом золотого сечения находим две точки и т.д. В результате получаем
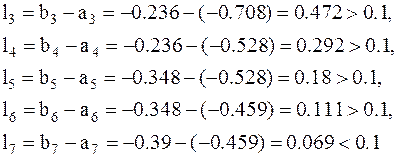
11. Следовательно, точка минимума приблизительно равна
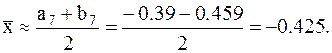
12. Вычисляем значение функции в этой точке
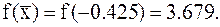
 2015-03-22
2015-03-22 758
758








