1. Основные определения. Обыкновенным дифференциальным уравнением называется уравнение, которое содержит производные от искомой функции y(x):
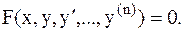 (9.1)
(9.1)
где x-независимая переменная, (n)-порядок производной. Наивысший порядок n, входящий в это уравнение называется порядком дифференциального уравнения.
Общее решение дифференциального уравнения имеет вид:
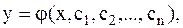 (9.2)
(9.2)
где с1,...,сn - произвольные постоянные. Их количество определяется порядком дифференциального уравнения. Если значения c1,...,cn - известны и соответственно равны 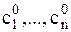 , то получаем частное решение:
, то получаем частное решение: 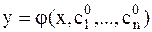 . Значения
. Значения 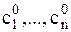 определяются из условий, которые называются дополнительными условиями для данного дифференциального уравнения.
определяются из условий, которые называются дополнительными условиями для данного дифференциального уравнения.
В зависимости от способа задания дополнительных условий для данного дифференциального уравнения существуют два различных типа задач: задача Коши и краевая задача. Дополнительные условия задаются значениями функции и ее производных при некоторых значениях переменной x, т.е. в некоторых точках отрезка, где требуется найти решение.
2. Задача Коши для дифференциального уравнения первого порядка. Если дополнительные условия задаются в одной точке, то такая задача называется задачей Коши. Дополнительные условия в задаче Коши называются начальными условиями, а точка x=x0, в которой они задаются - начальной точкой.
Рассмотрим задачу Коши для дифференциального уравнения первого порядка:
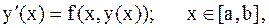 (9.3)
(9.3)
с начальным условием 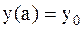 .
.
Решением дифференциального называется функция y(x), которая при подстановке его в уравнение, превращает последнее в тождество. График решения дифференциального уравнения называется интегральной кривой. Общее решение уравнения имеет вид: y=j(x,c1). Данному решению соответствует бесконечное семейство интегральных кривых с параметром c1. С помощью начальных условий y(x0)=y0 из этого семейства выделяется одна конкретная интегральная кривая, которая является частным решением.
Пусть выбраа произвольная интегральная кривая и на ней точка с координатами (xi,yi). В этой точке имеем: 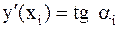 , где ai угол наклона касательной к интегральной кривой в заданной точке xi (Рис.9).
, где ai угол наклона касательной к интегральной кривой в заданной точке xi (Рис.9).
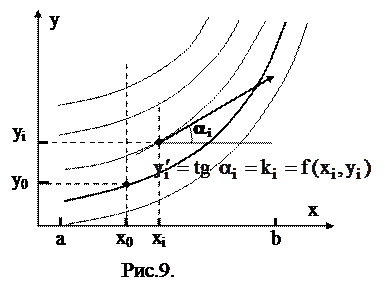 Величина
Величина 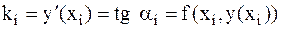 называется угловым коэффициентом. Угловой коэффициент в узле xi равен тангенсу угла наклона касательной к интегральной кривой, проходящей через точку (xi,yi).
называется угловым коэффициентом. Угловой коэффициент в узле xi равен тангенсу угла наклона касательной к интегральной кривой, проходящей через точку (xi,yi).
3. Методы Эйлера решения задачи Коши. На отрезке [a,b] вводится равномерная сетка: xi, i=0,1,...,n; с шагом h=xi+1-xi, при этом x0=a и xn=b. Сетка рассматривается как переменная величина xh, которая изменяется дискретным образом с шагом h между узлами. Набор значений функции yi=y(xi), i=0,1,...,n; в узлах xi называется сеточной функцией и обозначается как yh. Решение задачи Коши состоит в нахождении значений сеточной функции удовлетворяющей дифференциальному уравнению и заданным начальным условиям.
а) простой метод Эйлера первого порядка точности по шагу h. Для аппроксимации первой производной используем правую разность 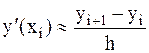 . В итоге получим формулу метода Эйлера для решения дифференциального уравнения:
. В итоге получим формулу метода Эйлера для решения дифференциального уравнения:
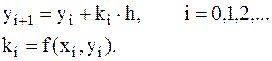 , (9.4)
, (9.4)
В узле xi вычисляется угловой коэффициент ki, с помощью которого вычисляется значение сеточной функции yi+1 в узле xi+1.
Так как значение y0 задано граничным условием: y0=y(x0), то приведенное соотношее позволяет определить значение сеточной функции yi во всех последующих узлах начиная с первого;
б) метод Эйлера-Коши второго порядка точности по шагу h. Расчетная формула данного метода имеет вид:
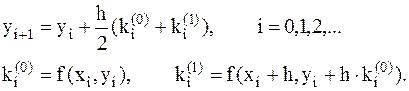 (9.5)
(9.5)
На первом этапе, в соответствии с методом Эйлера первого порядка точности, с помощью углового коэффициента 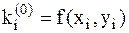 ) вычисляется грубое приближение искомой функции
) вычисляется грубое приближение искомой функции 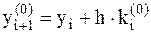 в узле xi+1=xi+h. Затем,в этом узле с помощью значений
в узле xi+1=xi+h. Затем,в этом узле с помощью значений 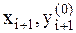 вычисляется угловой коэффициент
вычисляется угловой коэффициент 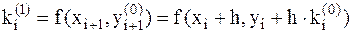 . Далее определяется усредненный угловой коэффициент
. Далее определяется усредненный угловой коэффициент 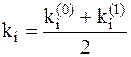 , который служит для вычисления значения yi+1=yi+h×ki;
, который служит для вычисления значения yi+1=yi+h×ki;
в) усовершенствованный метод Эйлера второго порядка точности по шагу h. Расчетная формула данного метода имеет вид:
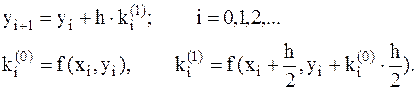 (9.6)
(9.6)
С помощью углового коэффициента: 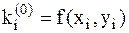 в узле
в узле 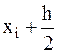 вычисляется приближенное значение
вычисляется приближенное значение 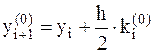 . Далее вычисляется угловой коэффициент
. Далее вычисляется угловой коэффициент 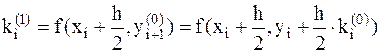 в этом узле. С помощью этого коэффициента вычисляется значение
в этом узле. С помощью этого коэффициента вычисляется значение 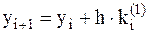 .
.
4. Метод Рунге - Кутты четвертого порядка точности. Наиболее известным из методов Рунге-Кутты является классический 4-этапный метод четвертого порядка точности, расчетные формулы которого имеют вид:

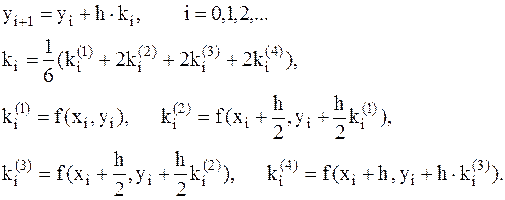 (9.7)
(9.7)
В начале один за другим вычисляются угловые коэффициенты 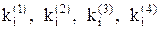 . Далее определяется угловойт
. Далее определяется угловойт 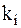 , с помощью которого находится значение сеточной функции
, с помощью которого находится значение сеточной функции 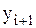 в узле
в узле 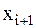 .
.
Варианты задания №12
Используя указанный метод на отрезке [a,b] с шагом h=0,2 численно решить дифференциальное уравнение при заданном начальном условии.
1. 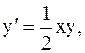 y(0)=1, a=0, b=1. (метод Эйлера-Коши)
y(0)=1, a=0, b=1. (метод Эйлера-Коши)
2. 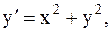 y(-1)=3, a=-1, b=0. (усоверш. метод Эйлера)
y(-1)=3, a=-1, b=0. (усоверш. метод Эйлера)
3. 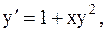 y(1)=0, a=1, b=2. (метод Рунге-Кутты)
y(1)=0, a=1, b=2. (метод Рунге-Кутты)
4. 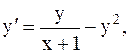 y(2)=1, a=2, b=3. (усоверш. метод Эйлера)
y(2)=1, a=2, b=3. (усоверш. метод Эйлера)
5. 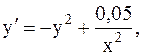 y(-3)=1, a=-3, b=-2. (метод Эйлера-Коши)
y(-3)=1, a=-3, b=-2. (метод Эйлера-Коши)
6. 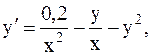 y(1)=0,5, a=1, b=2. (метод Рунге-Кутты)
y(1)=0,5, a=1, b=2. (метод Рунге-Кутты)
7. 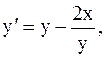 y(0)=1, a=0, b=1. (усоверш. метод Эйлера)
y(0)=1, a=0, b=1. (усоверш. метод Эйлера)
8. 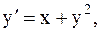 y(2)=0, a=2, b=3. (усоверш. метод Эйлера)
y(2)=0, a=2, b=3. (усоверш. метод Эйлера)
9. 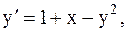 y(-1)=1, a=-1, b=0. (метод Эйлера-Коши)
y(-1)=1, a=-1, b=0. (метод Эйлера-Коши)
10. 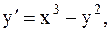 y(0)=0, a=0, b=1. (метод Эйлера-Коши)
y(0)=0, a=0, b=1. (метод Эйлера-Коши)
11. 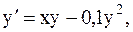 y(-2)=0,1; a=-2, b=-1. (метод Рунге-Кутты)
y(-2)=0,1; a=-2, b=-1. (метод Рунге-Кутты)
12. 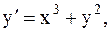 y(0)=0,5, a=0, b=1. (метод Рунге-Кутты)
y(0)=0,5, a=0, b=1. (метод Рунге-Кутты)
13. 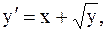 y(1)=0,7, a=1, b=1,5. (метод Эйлера-Коши)
y(1)=0,7, a=1, b=1,5. (метод Эйлера-Коши)
14. 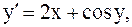 y(-1)=0, a=-1, b=0. (усоверш. метод Эйлера)
y(-1)=0, a=-1, b=0. (усоверш. метод Эйлера)
15. 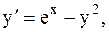 y(0)=0, a=0, b=1. (метод Рунге-Кутты)
y(0)=0, a=0, b=1. (метод Рунге-Кутты)
16. 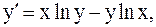 y(1)=2, a=1, b=2. (метод Эйлера-Коши)
y(1)=2, a=1, b=2. (метод Эйлера-Коши)
17. 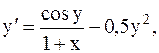 y(3)=0, a=3, b=4. (метод Эйлера-Коши)
y(3)=0, a=3, b=4. (метод Эйлера-Коши)
18. 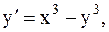 y(-1)=0, a=-1, b=0. (усоверш. метод Эйлера)
y(-1)=0, a=-1, b=0. (усоверш. метод Эйлера)
19. 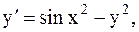 y(2)=0, a=2, b=3. (усоверш. метод Эйлера)
y(2)=0, a=2, b=3. (усоверш. метод Эйлера)
20. 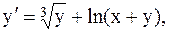 y(-2)=2, a=-2, b=-1. (метод Рунге-Кутты)
y(-2)=2, a=-2, b=-1. (метод Рунге-Кутты)
21. 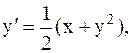 y(0)=1, a=0, b=1. (метод Эйлера-Коши)
y(0)=1, a=0, b=1. (метод Эйлера-Коши)
22. 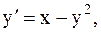 y(-1)=3, a=-1, b=0. (усоверш. метод Эйлера)
y(-1)=3, a=-1, b=0. (усоверш. метод Эйлера)
23. 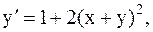 y(1)=0, a=1, b=2. (метод Рунге-Кутты)
y(1)=0, a=1, b=2. (метод Рунге-Кутты)
24. 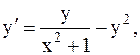 y(2)=1, a=2, b=3. (усоверш. метод Эйлера)
y(2)=1, a=2, b=3. (усоверш. метод Эйлера)
25. 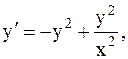 y(-3)=1, a=-3, b=-2. (метод Эйлера-Коши)
y(-3)=1, a=-3, b=-2. (метод Эйлера-Коши)
26. 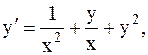 y(1)=0,5, a=1, b=2. (метод Рунге-Кутты)
y(1)=0,5, a=1, b=2. (метод Рунге-Кутты)
27. 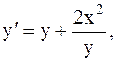 y(0)=1, a=0, b=1. (усоверш. метод Эйлера)
y(0)=1, a=0, b=1. (усоверш. метод Эйлера)
28. 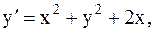 y(2)=0, a=2, b=3. (усоверш. метод Эйлера)
y(2)=0, a=2, b=3. (усоверш. метод Эйлера)
29. 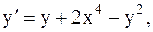 y(-1)=1, a=-1, b=0. (метод Эйлера-Коши)
y(-1)=1, a=-1, b=0. (метод Эйлера-Коши)
30. 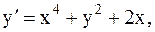 y(0)=0, a=0, b=1. (метод Эйлера-Коши)
y(0)=0, a=0, b=1. (метод Эйлера-Коши)
31. 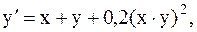 y(-2)=0,1; a=-2, b=-1.(метод Рунге-Кутты)
y(-2)=0,1; a=-2, b=-1.(метод Рунге-Кутты)
32. 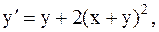 y(0)=0,5, a=0, b=1. (метод Рунге-Кутты)
y(0)=0,5, a=0, b=1. (метод Рунге-Кутты)
33. 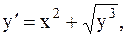 y(0,5)=0,72, a=0,5, b=1,5.(метод Эйлера-Коши)
y(0,5)=0,72, a=0,5, b=1,5.(метод Эйлера-Коши)
34. 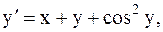 y(-1)=0, a=-1, b=0. (усоверш. метод Эйлера)
y(-1)=0, a=-1, b=0. (усоверш. метод Эйлера)
35. 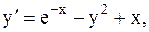 y(0)=0, a=0, b=1. (метод Рунге-Кутты)
y(0)=0, a=0, b=1. (метод Рунге-Кутты)
36. 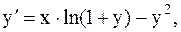 y(1)=2, a=1, b=2. (метод Эйлера-Коши)
y(1)=2, a=1, b=2. (метод Эйлера-Коши)
37. 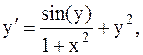 y(3)=0, a=3, b=4. (метод Эйлера-Коши)
y(3)=0, a=3, b=4. (метод Эйлера-Коши)
38. 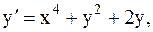 y(-1)=0, a=-1, b=0. (усоверш. метод Эйлера)
y(-1)=0, a=-1, b=0. (усоверш. метод Эйлера)
39. 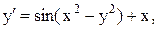 y(2)=0, a=2, b=3. (усоверш. метод Эйлера)
y(2)=0, a=2, b=3. (усоверш. метод Эйлера)
40. 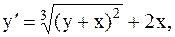 y(-2)=2, a=-2, b=-1. (метод Рунге-Кутты)
y(-2)=2, a=-2, b=-1. (метод Рунге-Кутты)
 2015-03-22
2015-03-22 1750
1750








