Метод наискорейшего спуска. Найти точку минимума функции 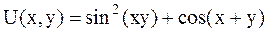 с точностью e=0,1 методом наискорейшего спуска.
с точностью e=0,1 методом наискорейшего спуска.
1. Находим градиент функции
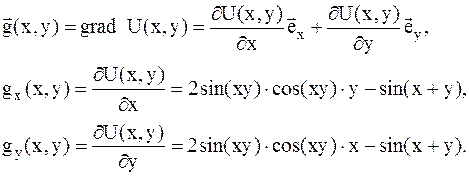
2. Выбираем нулевое приближение (точку 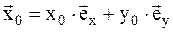 ):
): 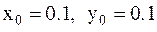
3. Вычисляем значение функции в этой точке и проекции градиента на оси x и y:
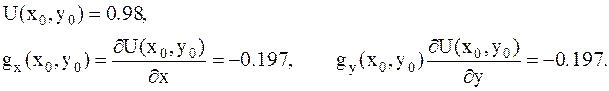 4. Выбираем параметр
4. Выбираем параметр  a: a=1. Находим координаты
a: a=1. Находим координаты 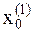 и
и 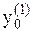 точки
точки 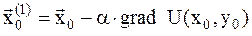 :
:
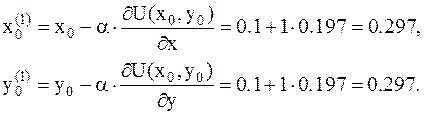
5. Вычисляем значение функции в этой точке: 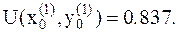
6. Так как значение функции U(x,y) в точке 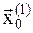 меньше, чем в точке
меньше, чем в точке 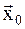 , то параметр a увеличиваем: a=2, находим
, то параметр a увеличиваем: a=2, находим 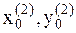 , вычисляем значение функции
, вычисляем значение функции 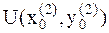 и сравниваем с предыдущим значением
и сравниваем с предыдущим значением 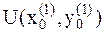 . Если функция убывает, то продолжаем увеличивать параметр a с шагом 1 до тех пор, пока функция убывает.
. Если функция убывает, то продолжаем увеличивать параметр a с шагом 1 до тех пор, пока функция убывает.
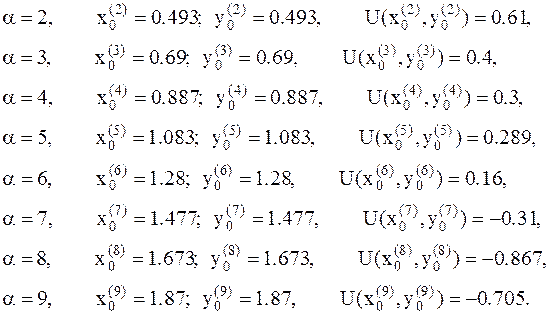
7. Так как в точке 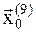 функция начинает возрастать, то минимум лежит между значениями a=7 и a=9. Таким образом, для параметра a имеем отрезок локализации
функция начинает возрастать, то минимум лежит между значениями a=7 и a=9. Таким образом, для параметра a имеем отрезок локализации 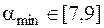 на котором находится минимум функции U(x,y).
на котором находится минимум функции U(x,y).
8. Применяем метод половинного деления для поиска минимума функции одной переменной 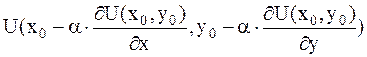 , где в качестве переменной выступает параметр a. Отрезок локализации делим попалам и определяем две точки
, где в качестве переменной выступает параметр a. Отрезок локализации делим попалам и определяем две точки 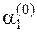 и
и 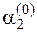 с учетом того, что e=0.1:
с учетом того, что e=0.1:
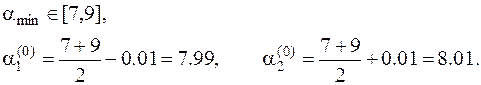
10. Вычисляем значения функции при этих значениях параметра a и проверяем третье условие (8.5): 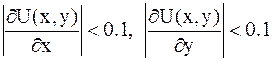 . Имеем
. Имеем
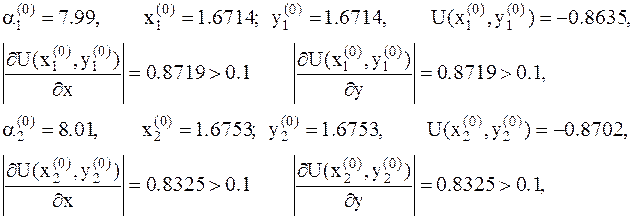
11. Условие (8.5) не выполнено, процесс продолжаем. Так как значение функции при 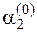 , т.е. в точке
, т.е. в точке 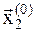 , меньше, то имеем новый отрезок локализации [7.99,9]. Процесс продолжаем:
, меньше, то имеем новый отрезок локализации [7.99,9]. Процесс продолжаем:
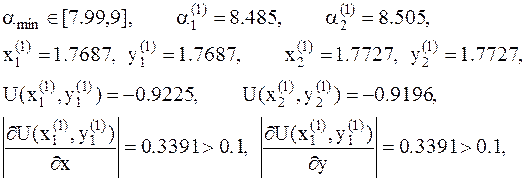
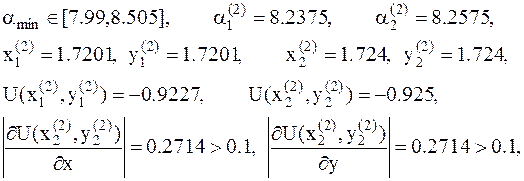
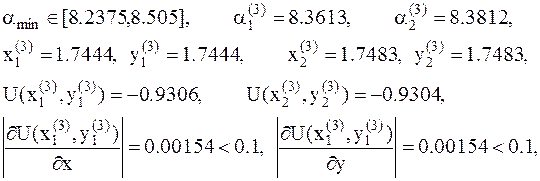
11. В точке 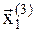 условие минимума выполнено, таким образом эта точка с координатами:
условие минимума выполнено, таким образом эта точка с координатами: 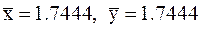 является точкой минимума, значение функции в этой точке равно:
является точкой минимума, значение функции в этой точке равно: 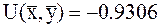 .
.
Метод деформированного многогранника. Найти точку минимума функции 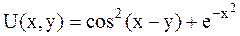 с точностью e=0,1 методом дефомированного многогранника.
с точностью e=0,1 методом дефомированного многогранника.
1. Так как функция зависит от двух переменных x,y, то имеем m=2. Выбираем шаг h=0.5 и три точки 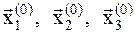 в соответствии с (8.8) с координатами:
в соответствии с (8.8) с координатами:
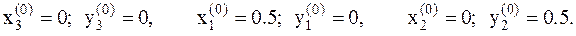
2. Вычисляем значение функции в этих точках. Имеем
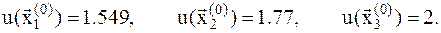
3. Значение функции в точке 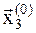 наибольшее, ее исключаем и находим среднюю точку из оставшихся точек, и кординаты пробной точки
наибольшее, ее исключаем и находим среднюю точку из оставшихся точек, и кординаты пробной точки 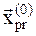 :
:
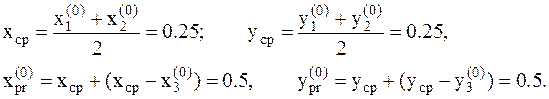
7. Вычисляем значение функции в пробной точке: 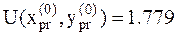 .
.
5. Сравниваем со значением в исключенной точке 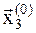 . Значение функции в пробной точке меньше, поэтому находим новую пробную точку
. Значение функции в пробной точке меньше, поэтому находим новую пробную точку 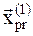 :
:
 Вычисляем в ней значение функции
Вычисляем в ней значение функции 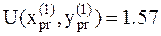 . Так как значение в пробной точке
. Так как значение в пробной точке 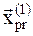 меньше, чем в пробной точке
меньше, чем в пробной точке 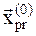 , то точку
, то точку 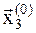 заменяем на пробную точку
заменяем на пробную точку 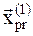 . Имеем опять три точки:
. Имеем опять три точки:
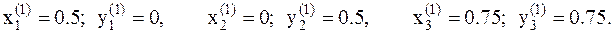 6. Вычисляем значение функции в этих точках и длины всех граней, выходящих из той точки, в которой функция имеет минимальное значение:
6. Вычисляем значение функции в этих точках и длины всех граней, выходящих из той точки, в которой функция имеет минимальное значение:
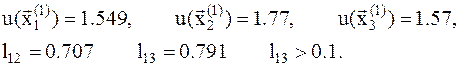
7. Так как значение функции в точке 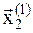 наибольшее, то ее исключаем и находим среднюю точку из оставшихся точек, и кординаты пробной точки:
наибольшее, то ее исключаем и находим среднюю точку из оставшихся точек, и кординаты пробной точки:
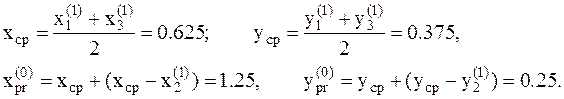
8. Вычисляем значение функции в пробной точке: 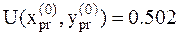 .
.
9. Сравниваем со значением в исключенной точке 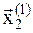 . Значение функции в пробной точке
. Значение функции в пробной точке 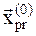 меньше, чем в точке
меньше, чем в точке 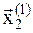 , поэтому находим новую пробную точку
, поэтому находим новую пробную точку 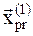 :
:

и вычисляем значение функции в этой точке, имеем 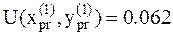
10. Так как значение функции в пробной точке 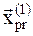 меньше, чем в пробной точке
меньше, чем в пробной точке 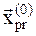 , то точку
, то точку 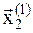 заменяем на пробную точку
заменяем на пробную точку  . В результате имеем три новые точки и значения функции в этих точках:
. В результате имеем три новые точки и значения функции в этих точках:
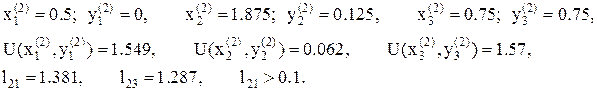 11. Процесс продолжаем, в результате имеем
11. Процесс продолжаем, в результате имеем
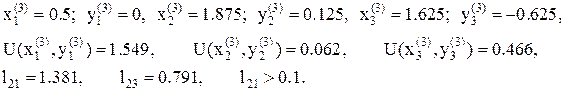
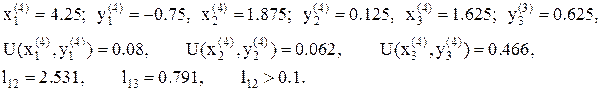
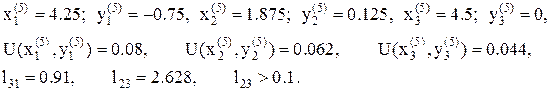
11. После четырех деформаций многогранник восстанавливаем. Так как в точке 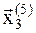 значение функции наименьшее, то ее берем за базовую точку, шаг уменьшаем в два раза и процесс продолжаем. Имеем:
значение функции наименьшее, то ее берем за базовую точку, шаг уменьшаем в два раза и процесс продолжаем. Имеем:
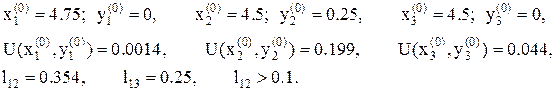
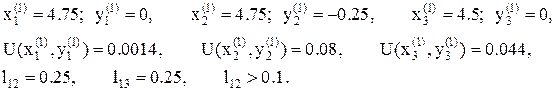
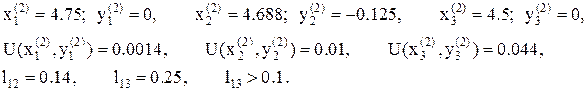
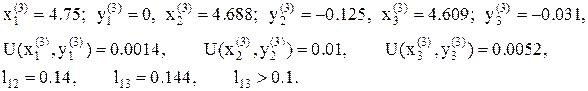
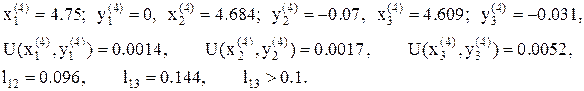
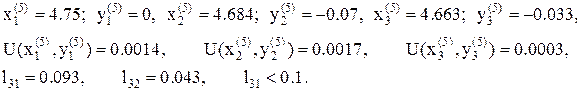
12. Условие минимума выполнено, так как длины всех сторон многогранника, выходящие из точки с координатами: 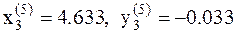 , в которой функция минимальна, меньше заданного e=0.1. Имеем точку минимума:
, в которой функция минимальна, меньше заданного e=0.1. Имеем точку минимума: 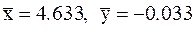 , значение функции U(x,y) в этой точке равно:
, значение функции U(x,y) в этой точке равно: 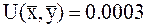 .
.
 2015-03-22
2015-03-22 775
775








