Зачастую, как для одномерных, так и для многомерных систем, уравнения, описывающие зависимость координат от входных воздействий с порядком, большим первого, приводят к системе уравнений первого порядка, у которых в левой части записана производная координаты, а в правой – линейная функция координат и управляющих воздействий без производных.
Рассмотрим на примере:
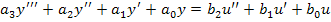
Разделим левую и правую части на 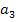
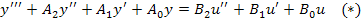
Обозначим 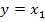 .
.
Чтобы учесть производные от управления, вводим новые функции следующего вида:
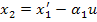
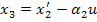 или
или 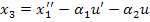
Тогда исходное уравнение 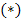 с заменой
с заменой 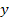 на
на 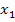 может быть записано:
может быть записано:
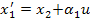
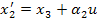
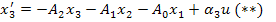
Чтобы определить коэффициенты 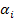 , подставим в уравнение
, подставим в уравнение 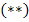 выражения для
выражения для 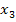 и
и 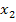 и сопоставим его с исходным уравнением
и сопоставим его с исходным уравнением
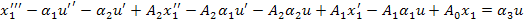
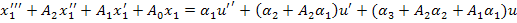
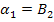
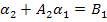 , t wx:val="Cambria Math"/><w:i/><w:sz w:val="24"/><w:sz-cs w:val="24"/><w:lang w:val="EN-US"/></w:rPr><m:t>О±</m:t></m:r></m:e><m:sub><m:r><w:rPr><w:rFonts w:ascii="Cambria Math" w:h-ansi="Cambria Math"/><wx:font wx:val="Cambria Math"/><w:i/><w:sz w:val="24"/><w:sz-cs w:val="24"/></w:rPr><m:t>1</m:t></m:r></m:sub></m:sSub></m:oMath></m:oMathPara></w:p><w:sectPr wsp:rsidR="00000000"><w:pgSz w:w="12240" w:h="15840"/><w:pgMar w:top="1134" w:right="850" w:bottom="1134" w:left="1701" w:header="720" w:footer="720" w:gutter="0"/><w:cols w:space="720"/></w:sectPr></w:body></w:wordDocument>">
, t wx:val="Cambria Math"/><w:i/><w:sz w:val="24"/><w:sz-cs w:val="24"/><w:lang w:val="EN-US"/></w:rPr><m:t>О±</m:t></m:r></m:e><m:sub><m:r><w:rPr><w:rFonts w:ascii="Cambria Math" w:h-ansi="Cambria Math"/><wx:font wx:val="Cambria Math"/><w:i/><w:sz w:val="24"/><w:sz-cs w:val="24"/></w:rPr><m:t>1</m:t></m:r></m:sub></m:sSub></m:oMath></m:oMathPara></w:p><w:sectPr wsp:rsidR="00000000"><w:pgSz w:w="12240" w:h="15840"/><w:pgMar w:top="1134" w:right="850" w:bottom="1134" w:left="1701" w:header="720" w:footer="720" w:gutter="0"/><w:cols w:space="720"/></w:sectPr></w:body></w:wordDocument>"> 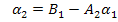
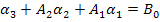 ,
, 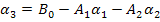
Если имеем в общем случае уравнение n-го порядка, причем порядок производных в правой части не выше n-1.
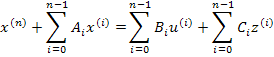
Тогда система уравнений в форме Коши будет записана т.о.:
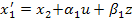
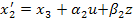
…
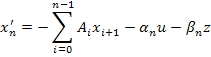
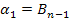
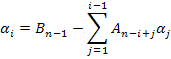
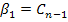
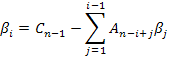
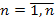
 2015-03-22
2015-03-22 2565
2565