Имеем однородное матричное дифференциальное уравнение в форме Коши: 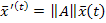
Будем искать решение в виде:
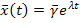
где 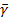 - вектор постоянных коэффициентов,
- вектор постоянных коэффициентов,
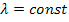 .
.
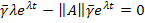
Вынесем вектор 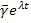 :
:
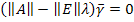
Чтобы в общем случае 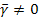 , необходимо, чтобы определитель разности
, необходимо, чтобы определитель разности 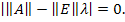
Это уравнение называется характеристическим уравнением для системы уравнений Коши. В развернутом виде:
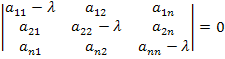
Если раскроем определитель, получим уравнение n-го порядка для 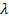 , решение которого даст n корней:
, решение которого даст n корней: 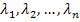 .
.
Количество корней равно рангу матрицы.
Подставляем 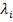 в уравнение
в уравнение 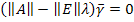
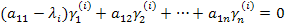
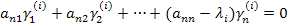
Если уравнения линейно зависимы, соответственно часть элементов вектора задаем, остальные находим. Подставляя поочередно все значения 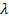 , определяем n векторов
, определяем n векторов 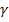 .
.
Тогда решения однородного уравнения можно записать:
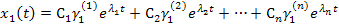
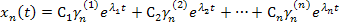
При 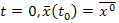 из этого условия находим постоянные С.
из этого условия находим постоянные С.
Фундаментальная матрица решений:
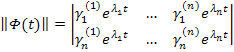
Проблема заключается в том, что найти нормированную фундаментальную матрицу решений путем приравнивания элементов матрицы 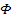 элементам матрицы
элементам матрицы 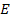 при
при 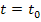 не приводит к результату.
не приводит к результату.
Чаще фундаментальную нормированную матрицу решений определяют:
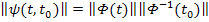
И тогда такую матрицу 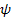 зачастую называют всюду нормированной.
зачастую называют всюду нормированной.
Если матрица 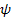 не особая, то:
не особая, то:
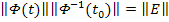
И тогда общее решение неоднородного дифференциального уравнения записывают как
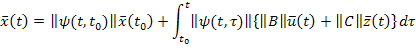
- формула Коши
Матрица фундаментальных решений 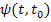 в качестве элементов содержит комбинацию решений исходной матрицы
в качестве элементов содержит комбинацию решений исходной матрицы 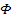 (для линейных систем сумма решений дифференциальных уравнений с различными коэффициентами также является решением).
(для линейных систем сумма решений дифференциальных уравнений с различными коэффициентами также является решением).
Для стационарных линейных систем (с постоянными коэффициентами):
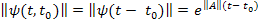
где функция
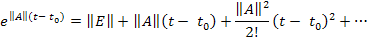
т.е. представлена бесконечным рядом.
В частном случае, когда матрица 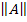 – диагональная,
– диагональная,
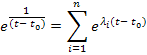
Получение общего решения модифицированного уравнения через фундаментальную матрицу решений однородного уравнения достаточно просто реализуется путем использованием метода неопределенных множителей
Рассмотрим пример:
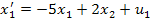
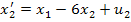
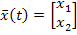
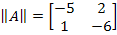
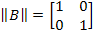
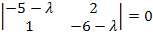
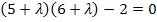
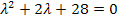
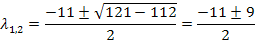
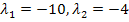
Находим вектор 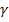 :
:
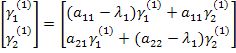
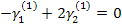
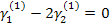
Поскольку оба уравнения одинаковые, то задаем 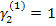 , тогда
, тогда 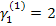 .
.
Аналогично подставляем 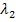 :
:
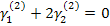
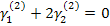
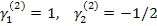
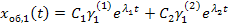
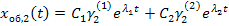
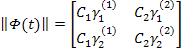
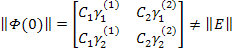 нормированная матрица не получена, поэтому используют другой метод.
нормированная матрица не получена, поэтому используют другой метод.
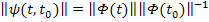
Рассмотрим случай, когда 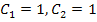 :
:
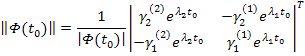
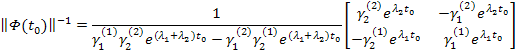
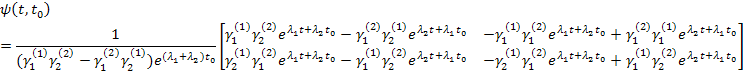
При 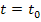 1-й элемент (
1-й элемент (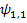 ) с учетом множителя перед матрицей определителя будет равен
) с учетом множителя перед матрицей определителя будет равен 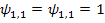 ,
,
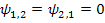
Если все элементы матрицы 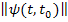 разделить на
разделить на 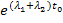 , то
, то
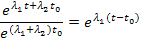
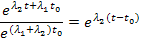
т.е. 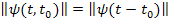
Это справедливо в том случае, если корни различные и действительные. Если корни комплексные, нужно переходить к тригонометрическим функциям.
 2015-03-22
2015-03-22 2155
2155








