С оценкой

Изм.

Лист

№ докум.

Подпись

Дата

Лист

КР-СМ-НГТУ-12КС3-012-15

Разраб.

Иванов И.И.

Провер.

Дербасов А.Н.

Н. Контр.

Утверд.

Курсовая работа по сопротивлению материалов

Лит.

Листов

??

Кафедра АГПМ и СМ

СОДЕРЖАНИЕ

Стр.

Введение
1. Определение перемещений и расчеты на прочность и жесткость статически определимых элементов конструкций…………………………
1.1 Расчет бруса при растяжении и сжатии………………………….....
1.2 Расчет бруса при кручении………………………………………….
1.3 Расчёт бруса при изгибе……………………………………………..
1.4 Расчет плоской рамы на изгиб………………………………………
1.5 Расчет плоско-пространственной рамы на изгиб и кручение
2. Расчет на прочность и жесткость статически неопределимых элементов конструкций………………………………………………………...
2.1 Расчет бруса при кручении………………………………………….
2.2 Расчёт бруса при изгибе……………………………………………..
2.3 Расчёт плоской рамы на изгиб………………………………………
3. Устойчивость сжатых стержней……………………………………...
3.1 Определение величин критической, допускаемой сил и коэффициента запаса на устойчивость для сжатого стержня……………….
4. Расчет на прочность и жесткость элементов конструкций при динамическом нагружении……………………………………………...
4.1 Определение из условия прочности допустимую угловую скорость вращения рамной конструкции……………………………………..
4.2 Расчёт рамы при ударном нагружении……………………………..
Заключение……………………………………………………………….
Список литературы………………………………………………………

Изм.

Лист

№ докум.

Подпись

Дата

Лист

КР-СМ-НГТУ-12КС3-012-15

ВВЕДЕНИЕ

Пояснительная записка содержит ___ листов, ___ рисунков, ___ таблицы, ___ приложений, список использованных источников − ___ наименований.

Актуальность работы. Одной из основных задач техники является обеспечение прочности инженерных конструкций и их элементов при наименьшей затрате материала. При проектировании различных инженерных конструкций приходится определять размеры их отдельных элементов. Эта задача решается на основе расчетов, цель которых – создание прочной, жесткой, устойчивой, долговечной и, вместе с тем экономичной конструкции. Такая задача возникает при проектировании машин, автомобилей, самолетов, судов, ракет и т.п.

Ключевые слова: растяжение, сжатие, кручение, изгиб, моменты инерции, устойчивость, внешняя сила, внутренняя сила, напряжение, деформация, перемещение.

Рассматриваемый объект: конструктивные элементы инженерных сооружений, нагруженные внешними силами.

Цель работы − произвести расчёт на прочность, жёсткость, устойчивость и динамические нагрузки элементов конструкций.

В процессе работы проводился расчёт на прочность, жёсткость, устойчивость и динамические нагрузки стержневых систем, работающих в условиях растяжения, сжатия, кручения, изгиба.

1. Определение перемещений и расчеты на прочность и жесткость статически определимых элементов конструкций

Задание № 12

Выполнил: студент гр. 12-КС-3

Иванов И.И.

Принял: к.т.н., доцент

Дербасов А.Н.

Номер схемы						Средний балл
Оценка
Подпись

Изм.

Лист

№ докум.

Подпись

Дата

Лист

КР-СМ-НГТУ-12КС3-012-15

1.1 Расчёт при растяжении и сжатии бруса

1.1.1 Условие задачи

Для бруса квадратного поперечного сечения (схема 5) и выполненного из стали Ст.3 в общем виде определить перемещения сечений B, C и D и построить эпюру перемещений. Подобрать размеры поперечного сечения бруса из условий прочности и жесткости ().

1.1.2 Краткие теоретические сведения

Перемещение любого сечения бруса при его растяжении-сжатии определяется методом Мора по формуле

,

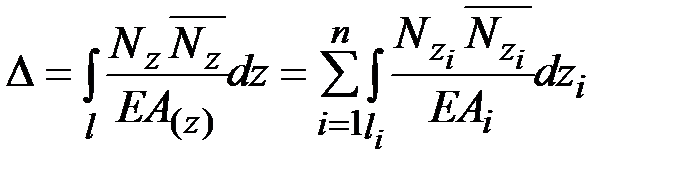где 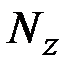– продольная сила в грузовом (исходном) состоянии;

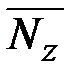– продольная сила в единичном состоянии;

Е – модуль упругости материала при растяжении-сжатии;

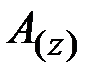– площадь поперечного сечения бруса;

n – число участков.

1.1.3 Решение задачи

а) Строим эпюры и аналитические выражения продольной силы в грузовом состоянии по участкам (Рис.1)

.

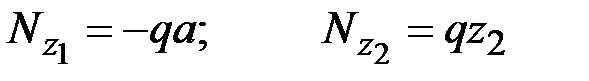б) Вычисляем перемещения сечений B, C и D в общем виде и строим эпюру продольных перемещений сечений (Рис. 1):

Сечение B

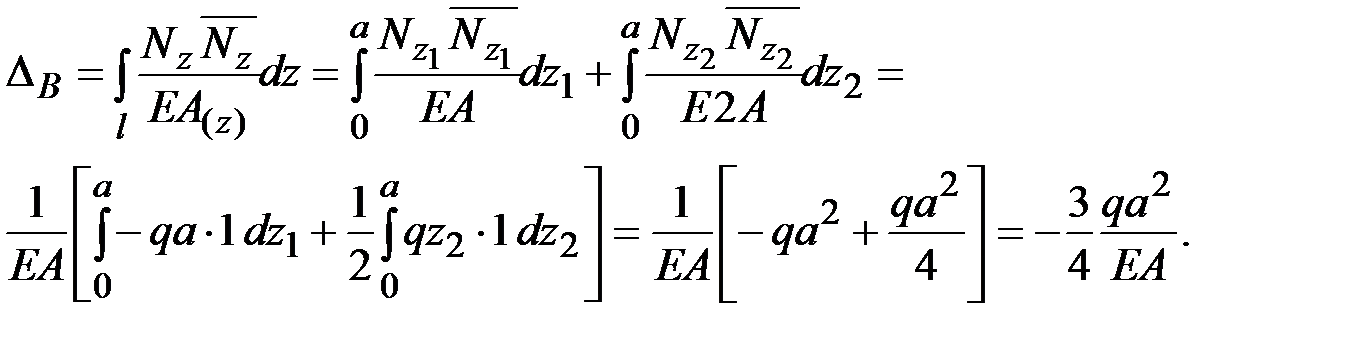
Знак минус указывает, что сечение В перемещается в сторону противо-положную единичной силе 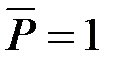в этом сечении, т.е. влево.

Сечение C

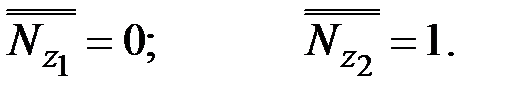
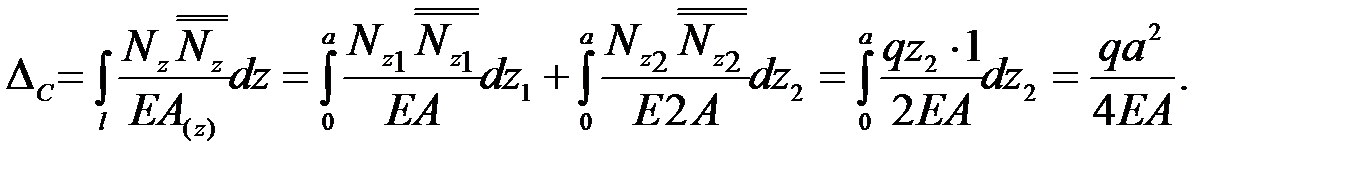
Знак плюс говорит о т

Изм.

Лист

№ докум.

Подпись

Дата

Лист

КР-СМ-НГТУ-12КС3-012-15

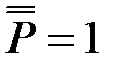ом, что сечение С переместится в направлении единичной силы , т.е. вправо.

Сечение D

Изм.

Лист

№ докум.

Подпись

Дата

Лист

КР-СМ-НГТУ-12КС3-012-15

Перемещение сечения D равно нулю, т.к. там заделка.

Характерной особенностью эпюры перемещений является отсутствие на ней скачков. Скачок означает либо зазор в этом сечении, либо разрушение.

в) Определяем размеры поперечного сечения из условия прочности в опасном сечении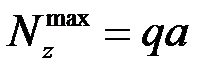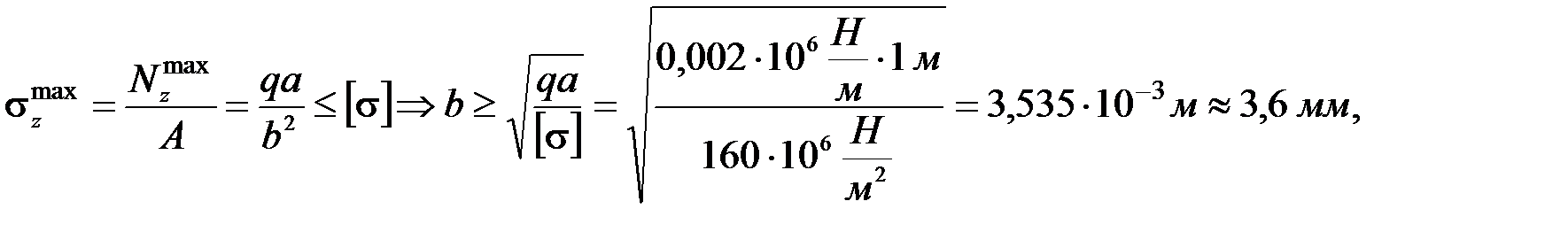, где

где 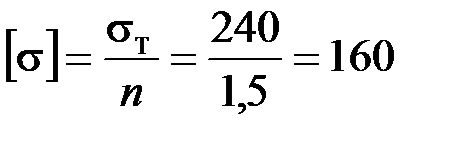МПа – допускаемые напряжения для стали Ст.3.

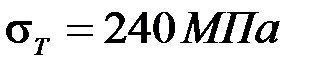– предел текучести стали Ст.3.

г) Определяем размеры поперечного сечения из условия жесткости

,

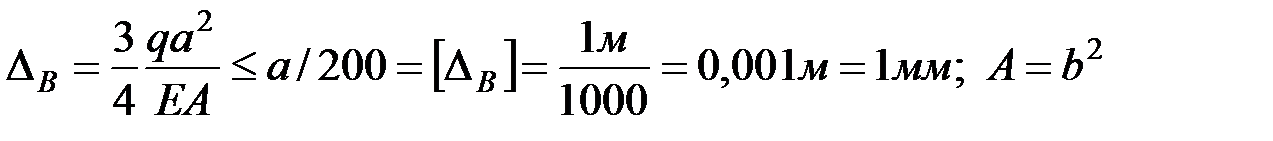отсюда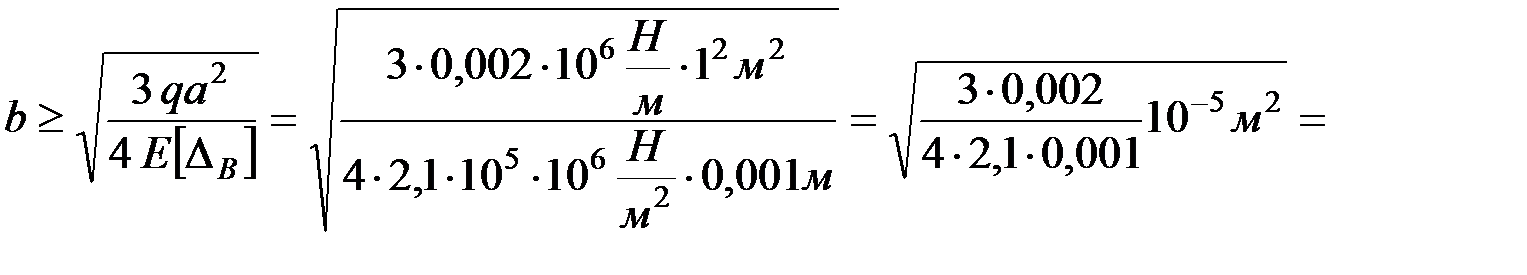

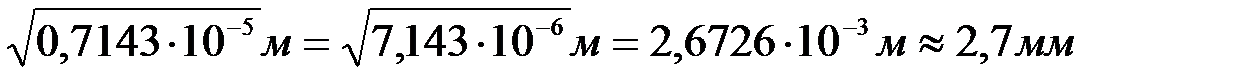
Из двух размеров квадратного сечения выбираем наибольший, как удовлетворяющий условиям прочности и жесткости, т.е. принимаем b= 3,6мм.

д) Для проверки правильности вычислений подсчитаем напряжение и перемещение для принятого размера квадратного сечения и сравниваем их с допускаемыми:

условие прочности < ;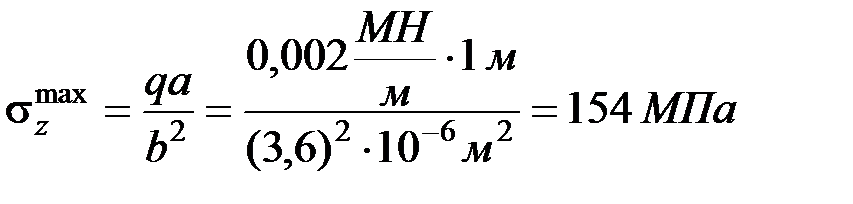

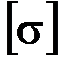условие жесткости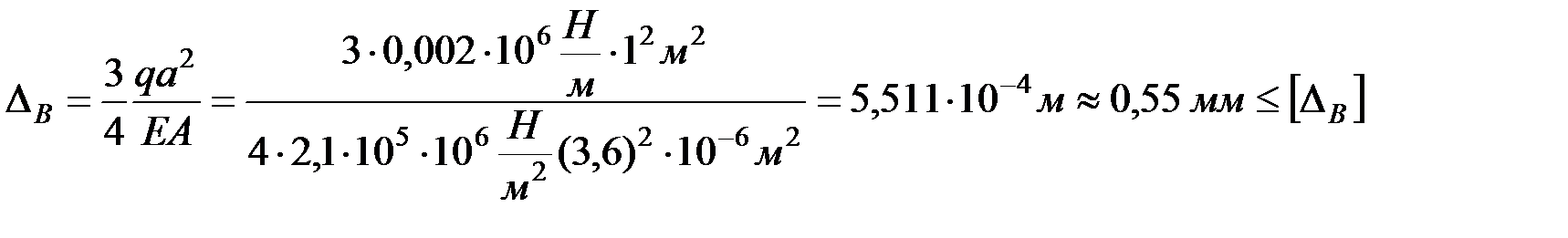

Примечание. Предполагается, что данная расчетная схема моделирует, очевидно, ползунковое или поршневое устройство, где потеря устойчивости бруса в сжатой зоне исключена направляющими стенками устройства.

Изм.

Лист

№ докум.

Подпись

Дата

Лист

КР-СМ-НГТУ-12КС3-012-15

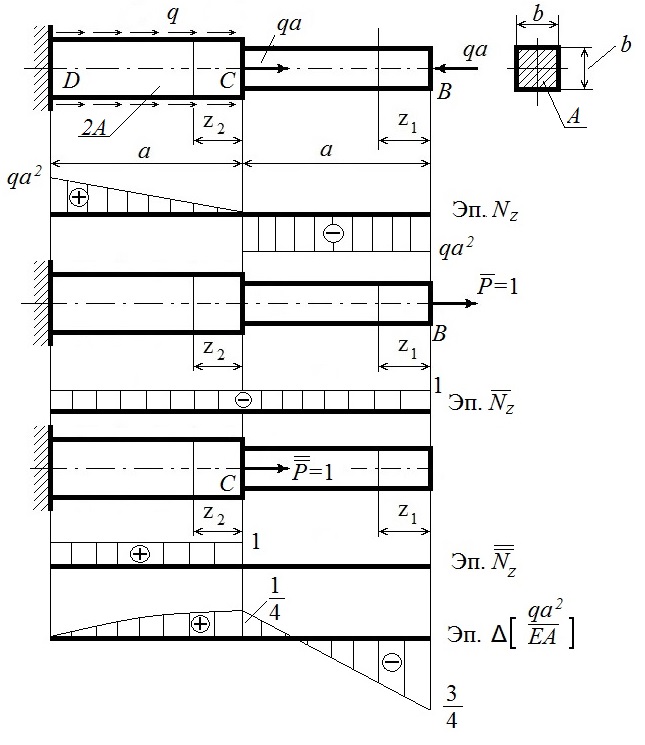
Рисунок 1. К расчёту бруса на растяжение и сжатие

Изм.

Лист

№ докум.

Подпись

Дата

Лист

КР-СМ-НГТУ-12КС3-012-15

1.2 Расчет бруса при кручении

1.2.1 Условие задачи

Для бруса (схема 33) круглого сплошного поперечного сечения, выполненного из алюминиевого сплава Д-16, подсчитать в общем виде углы поворота характерных сечений, построить эпюру углов закручивания относительно сечения С и подобрать диаметр бруса из условий прочности и жесткости ([q] =0,005 рад/м).

1.2.2 Краткие теоретические сведения.

Углы поворота сечений (углы закручивания) при кручении определяются методом Мора по формуле

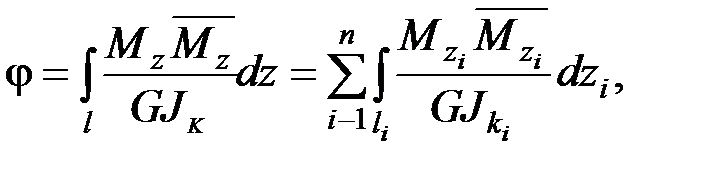
где 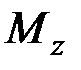– крутящий момент в грузовом (исходном) состоянии бруса;

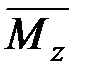– крутящий момент в единичном состоянии бруса;

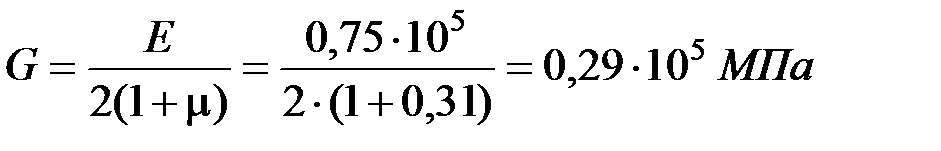– модуль упругости алюминиевого сплава Д-16 при сдвиге;

µ = 0,31 МПа ‒ коэффициент Пуассона алюминиевого сплава Д-16;

Е = 0,75·10⁵ Мпа ‒ модуль Юнга алюминиевого сплава Д-16;

n ‒ число участков.

1.2.3 Решение задачи

а) Строим эпюры и аналитические выражения крутящего момента в грузовом состоянии по участкам (Рис. 2)

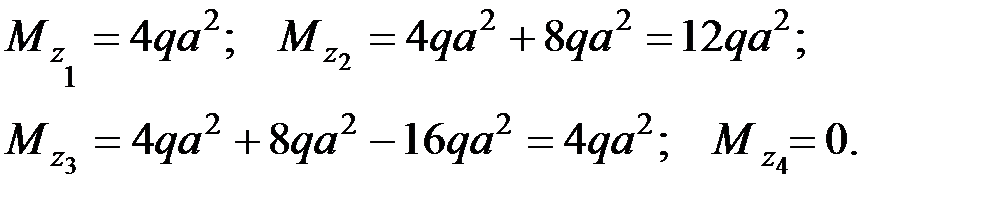
б) Вычисляем углы закручивания сечений А, В, D, Е относительно сечения С, принятого условно за неподвижное, в общем виде и строим эпюру углов закручивания (Рис. 2):

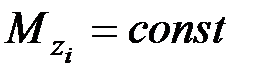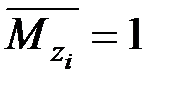Так как в пределах каждого участка , а , то .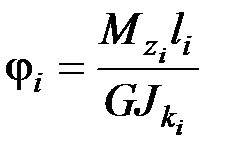

Сечение А:

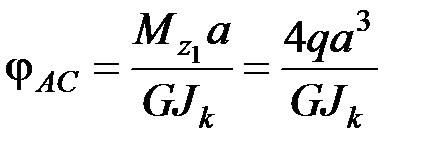‒ угол поворота сечения А относительно сечения С.

Сечение В:

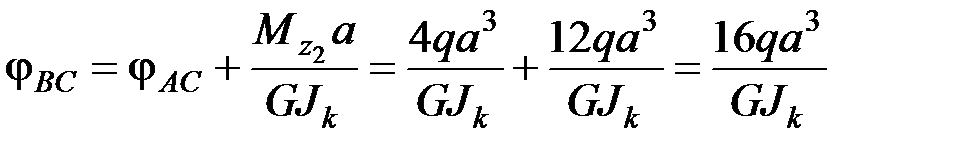‒ угол поворота сечения В относительно сечения С.

Изм.

Лист

№ докум.

Подпись

Дата

Лист

КР-СМ-НГТУ-12КС3-012-15

Сечение D:

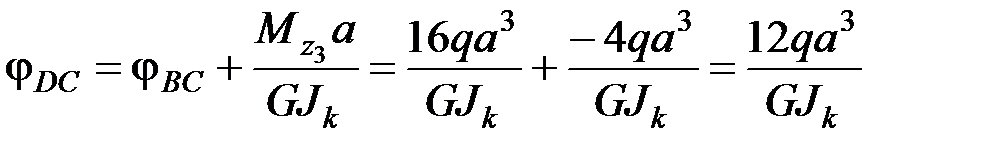‒ угол поворота сечения D относительно сечения С.

Сечение Е:

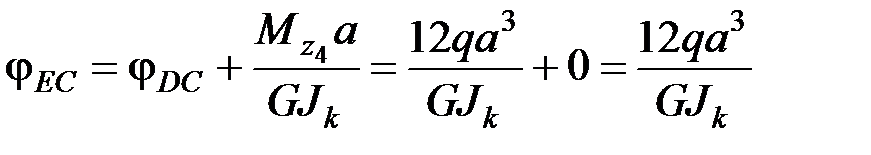‒ угол поворота сечения Е относительно сечения С.

в) Определяем диаметр бруса из условия прочности при кручении

,

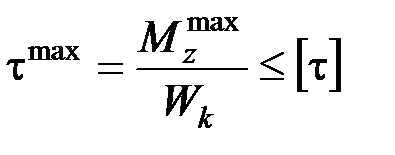где 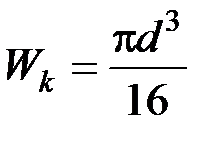‒ момент сопротивления круглого бруса сплошного сечения при кручении;

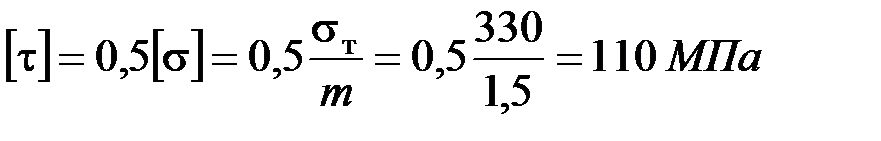‒ допускаемые касательные напряжения.

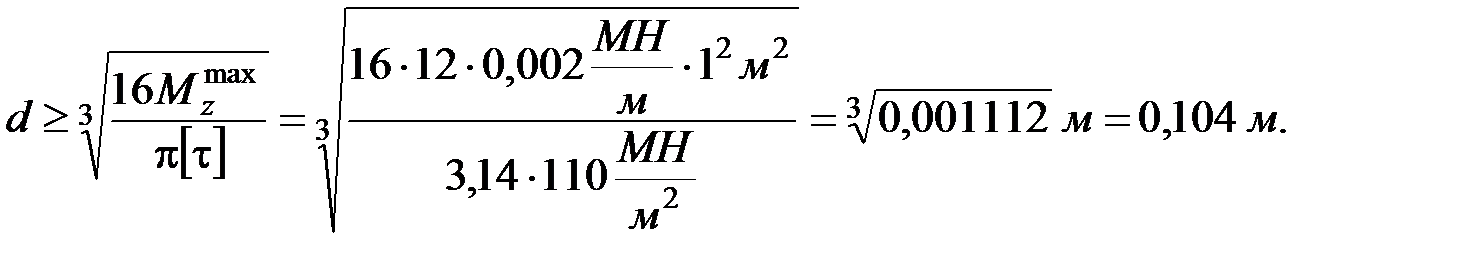
г) Находим диаметр бруса из условия жесткости при кручении

,

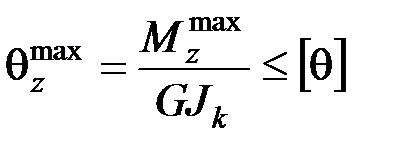где 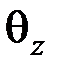‒ относительный угол закручивания, т.е. угол закручивания на единицу длины бруса;

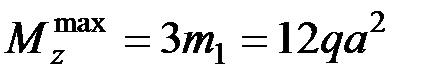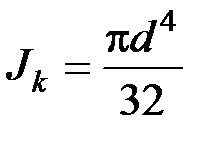, ‒ момент инерции поперечного круглого сплошного сечения бруса.

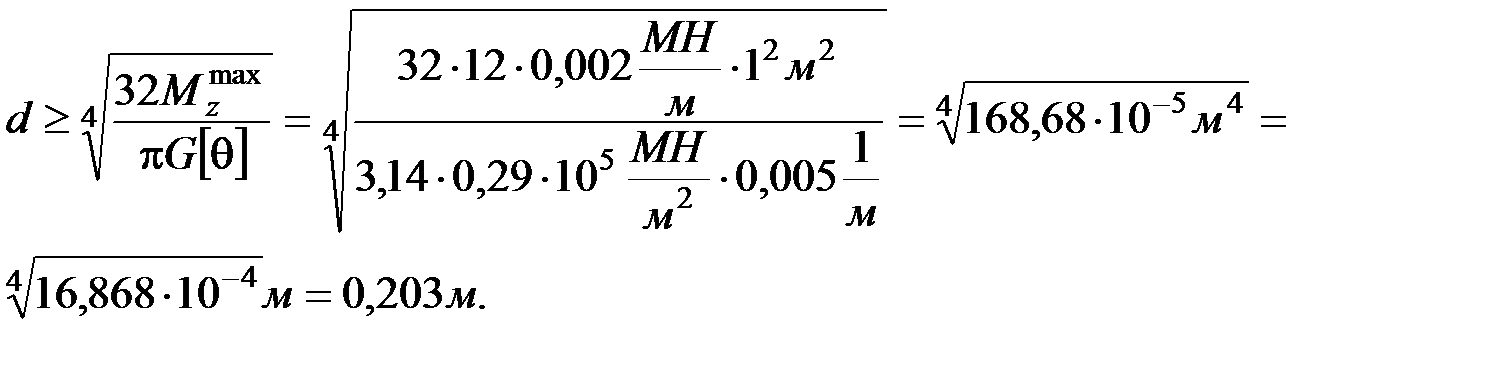
Из двух диаметров выбираем наибольший, как удовлетворяющий условиям прочности и жесткости, т.е. принимаем d= 0,203 м.

д) Для проверки правильности вычислений подсчитаем напряжение и относительный угол закручивания для принятого диаметра и сравниваем их с допускаемыми:

условие прочности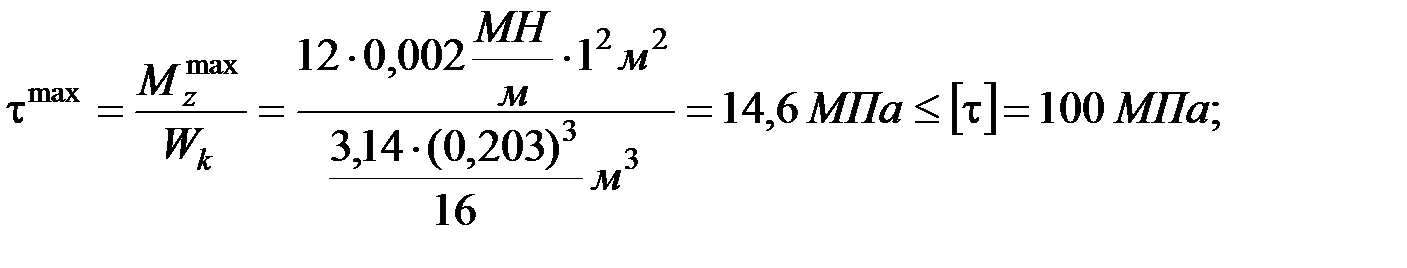

условие жесткости

Изм.

Лист

№ докум.

Подпись

Дата

Лист

КР-СМ-НГТУ-12КС3-012-15

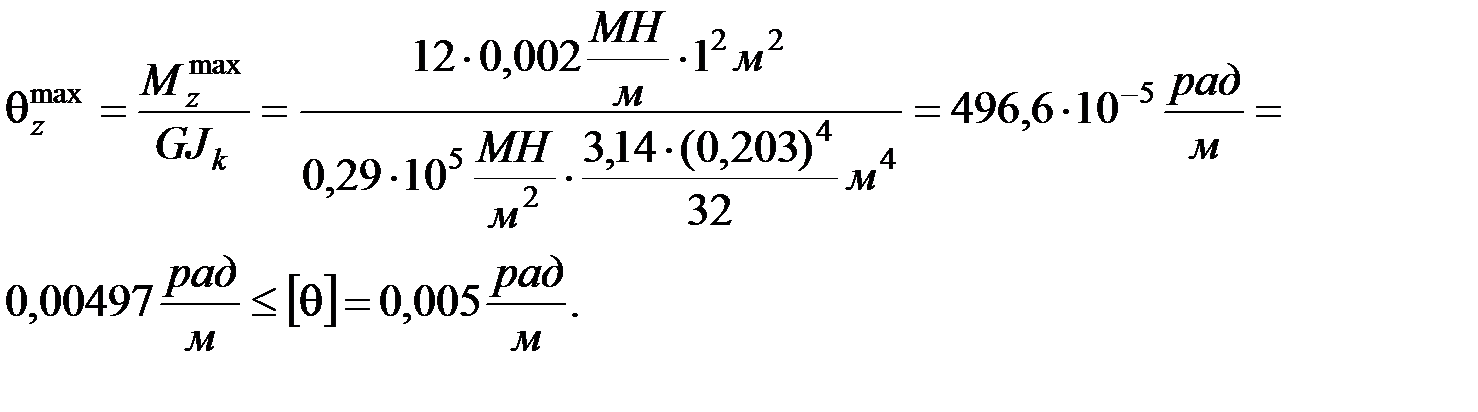
Изм.

Лист

№ докум.

Подпись

Дата

Лист

КР-СМ-НГТУ-12КС3-012-15

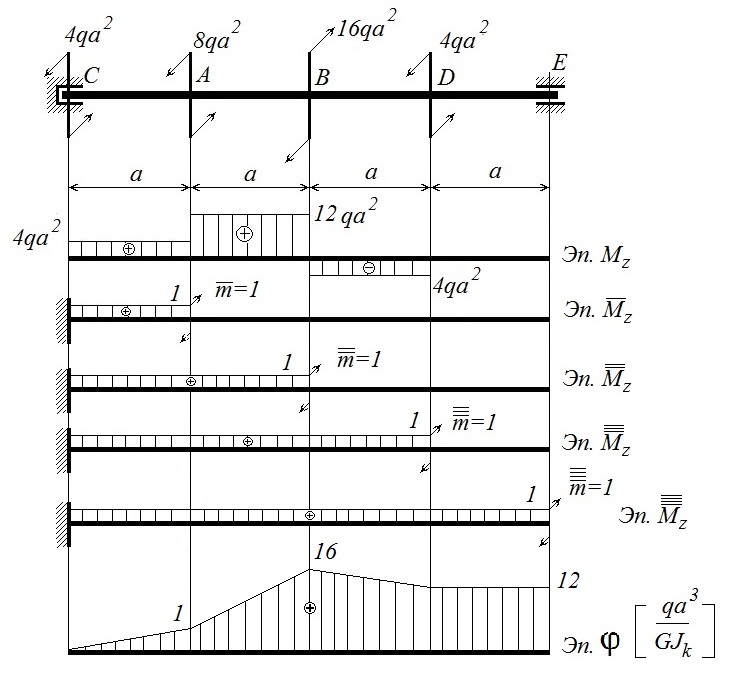
Рисунок 2. К расчету статически определимого бруса на кручение

1.3 Определение перемещений и расчеты на прочность и жесткость статически определимой балки при изгибе.

1.3.1 Условие задачи

Для двухопорной балки (схема 35), выполненной из стали Ст.3, имеющей постоянное по длине прямоугольное сечение (h / b= 2), в общем виде определить методом Мора прогиб в сечении С, способом Верещагина прогибы в сечениях C и D и угол поворота на правой опоре. Из условий прочности и жесткости (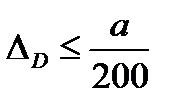) определить размеры поперечного сечения балки. Используя вид эпюры Mx и вычисленные значения прогибов и угла поворота при найденных размерах поперечного сечения, показать для балки характер изогнутой оси с указанием перемещений сечений C и D и угла поворота на правой опоре.

1.3.2 Краткие теоретические сведения

При изгибе балки возникают два типа перемещений - линейное перемещение (прогиб) и угловое перемещение (угол поворота сечения). Для определения перемещений балки при изгибе применяем метод Мора

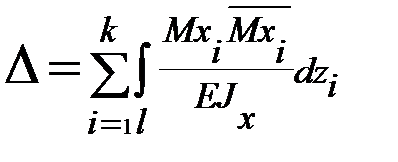-выражение для определения перемещения методом Мора (интеграл Мора);

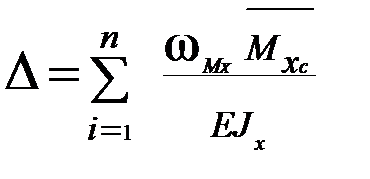- выражение для вычисления интеграла Мора способом Верещагина,

где - перемещение балки при изгибе;

k- количество силовых участков;

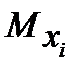-выражение изгибающих моментов по участкам балки в грузовом состоянии;

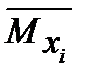- выражение изгибающих моментов по участкам балки в единичном состоянии;

Е 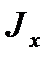- жесткость балки при изгибе;

n – количество элементов площади грузовой эпюры М_х;

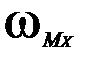- площадь элемента площади грузовой эпюры М_х;

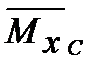- ордината единичной эпюры 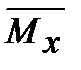, взятая под центром тяжести элемента площади грузовой эпюры М_х.

1.3.3 Решение задачи

1) Зададим единичные состояния: I ед. с. в сечении С (Р =1), II ед. с. в сечении D (Р =1),

Изм.

Лист

№ докум.

Подпись

Дата

Лист

КР-СМ-НГТУ-12КС3-012-15

III ед. с. на правой опоре B (M =1), (рис.3).

2) Определяем реактивные усилия на опорах из уравнений статического равновесия в грузовом состоянии и единичных состояниях (рис.3).

Грузовое состояние:

Изм.

Лист

№ докум.

Подпись

Дата

Лист

КР-СМ-НГТУ-12КС3-012-15

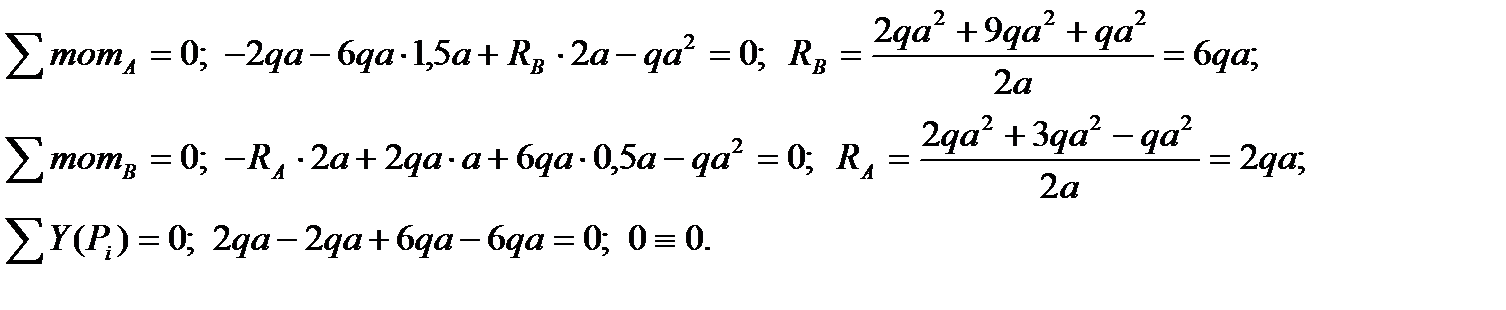
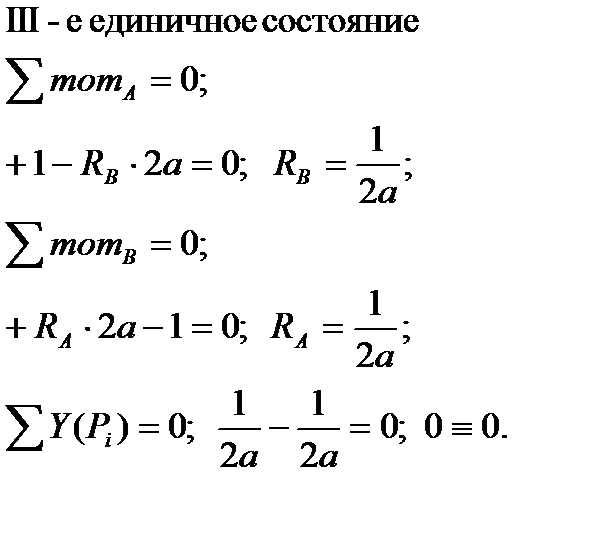3) Запишем выражения для изгибающих моментов в грузовом и единичных состояниях (таблица 1);

4) Построим эпюры перерезывающих сил и изгибающих моментов в грузовом состоянии и эпюры изгибающих моментов в единичных состояниях (рис.).

5) Определим прогиб в сечении C методом Мора.

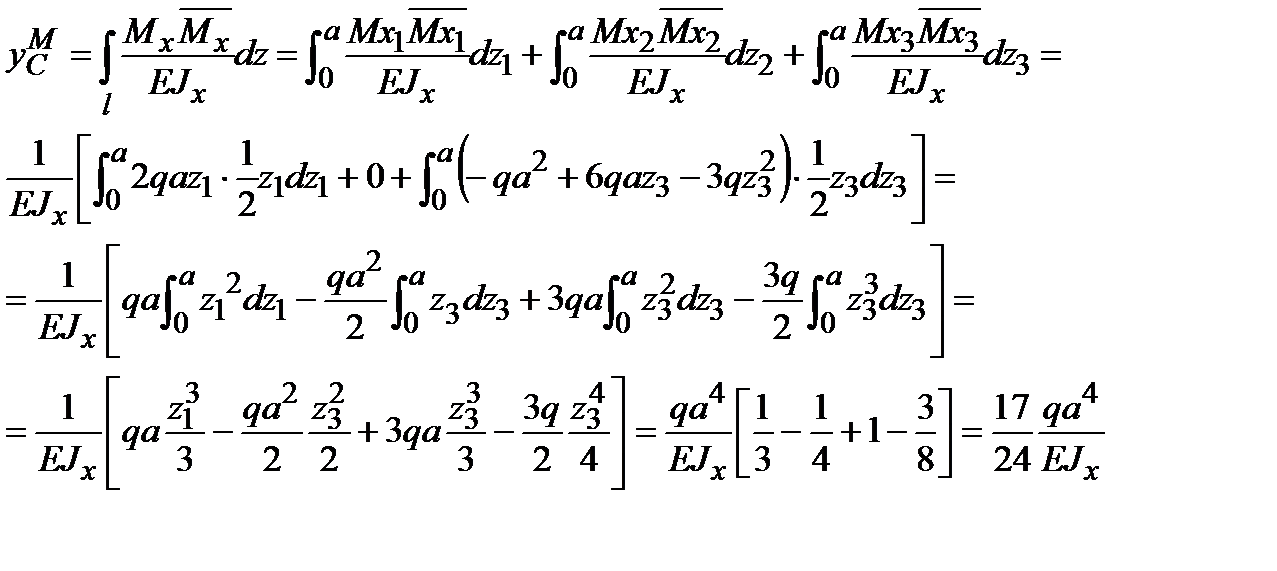
6) Определим прогибы в сечениях Cи D, а также угол поворота на опоре B способом Верещагина. Для этого разобьем грузовую эпюру изгибающих моментов на элементы 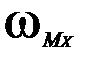, а на единичных эпюрах определим ординаты 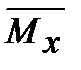, , 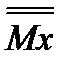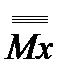(см. рис. 3 и таблица 2.).

Изм.

Лист

№ докум.

Подпись

Дата

Лист

КР-СМ-НГТУ-12КС3-012-15

Т а б л и ц а 1

Выражения для изгибающих моментов в грузовом и единичных состояниях

Грузовое состояние	I-е единич. состояние	II-е единичное состояние	III-е единичное состояние
I участок: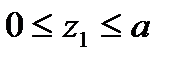
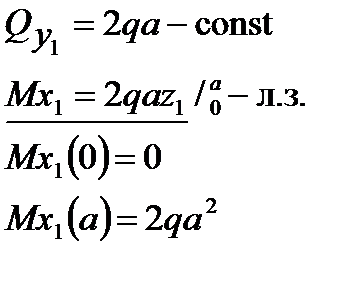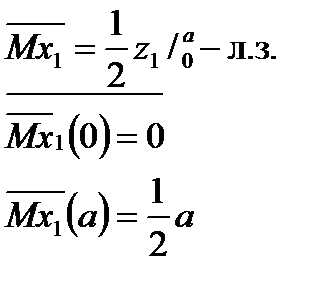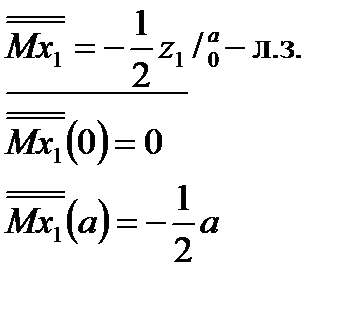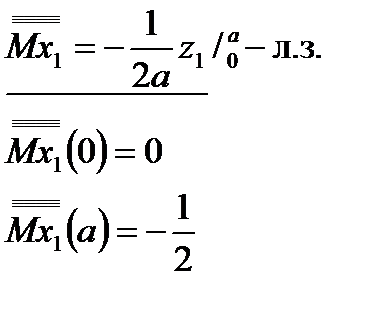II участ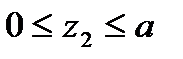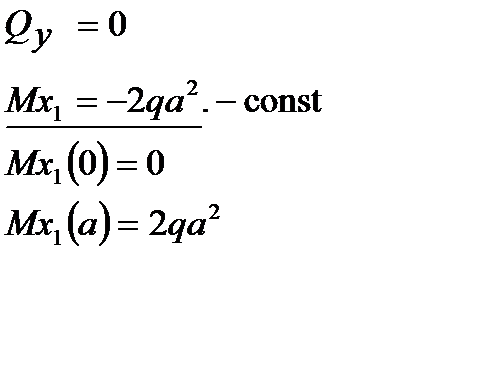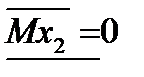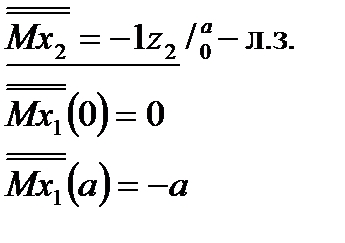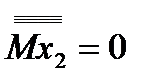ок:
III участок: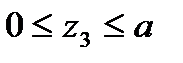

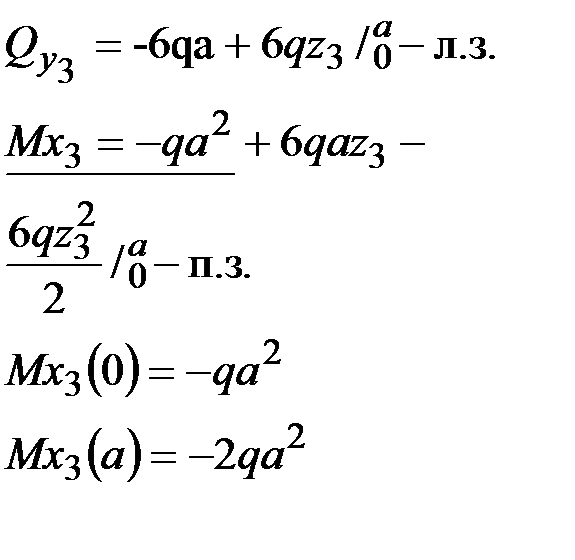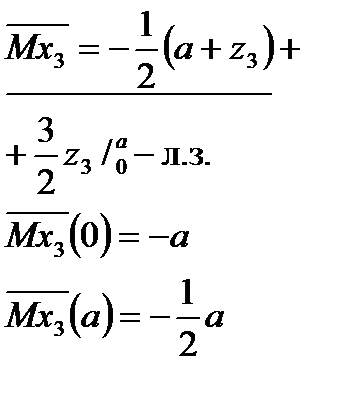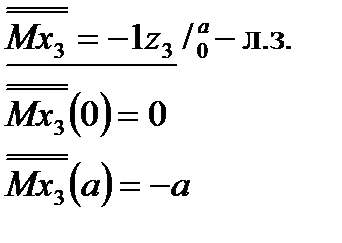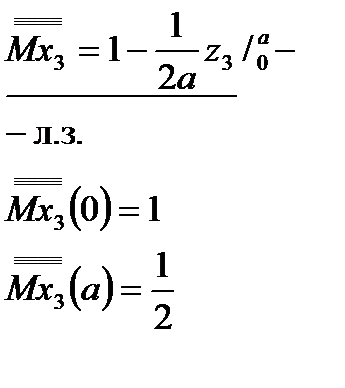Изм.

Лист

№ докум.

Подпись

Дата

Лист

КР-СМ-НГТУ-12КС3-012-15