Пусть две прямые 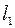 и
и 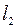 заданы уравнениями с угловыми коэффициентами
заданы уравнениями с угловыми коэффициентами 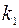 и
и 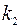 , соответственно, то есть
, соответственно, то есть 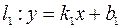 ;
; 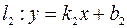 . Требуется найти угол
. Требуется найти угол 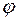 , на который надо повернуть прямую
, на который надо повернуть прямую 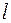 , вокруг точки их пересечения до совпадения с прямой
, вокруг точки их пересечения до совпадения с прямой  . (См. рис.27)
. (См. рис.27)
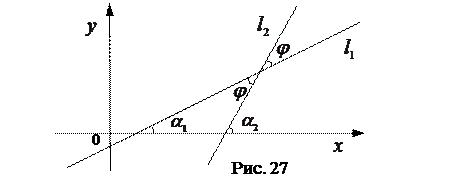
По теореме о внешнем угле треугольника, имеем: 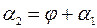 или
или 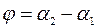 . Если
. Если 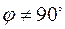 , то
, то
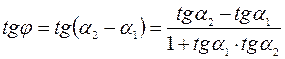 .
.
Но так как 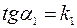 и
и 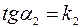 , то
, то
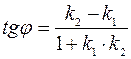 (3.8)
(3.8)
Таким образом, формула (3.8) позволяет находить угол между двумя прямыми на плоскости.
Пример. Найти угол между прямыми 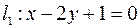 и
и 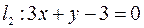 .
.
Решение. Запишем общее уравнение заданных прямых 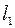 и
и 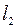 в виде уравнений с угловыми коэффициентами
в виде уравнений с угловыми коэффициентами 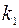 и
и 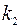 , соответственно:
, соответственно:
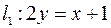 или
или 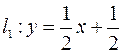 , значит
, значит 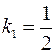 ;
;
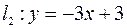 , значит
, значит 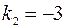 .
.
Подставляя найденные значения 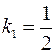 и
и 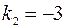 в формулу (3.8), находим угол
в формулу (3.8), находим угол 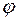 между прямыми
между прямыми 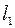 и
и 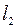 :
:
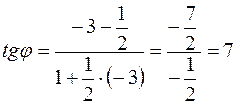 , откуда
, откуда 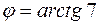 .
.
Ответ: 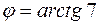 .
.
Заметим, что если требуется вычислить острый угол между прямыми, то правая часть формулы (3.8) берется по модулю, то есть
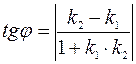 .
.
Если прямые 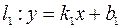 ;
; 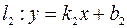 параллельны, то
параллельны, то 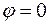 и
и 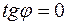 , следовательно, из формулы (3.8) получаем, что
, следовательно, из формулы (3.8) получаем, что 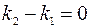 , то есть
, то есть 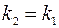 . И обратно, если прямые
. И обратно, если прямые 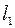 и
и 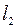 таковы, что
таковы, что 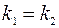 , значит
, значит 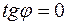 , то есть прямые параллельны.
, то есть прямые параллельны.
Если прямые 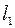 и
и 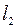 перпендикулярны, то
перпендикулярны, то 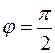 , следовательно
, следовательно 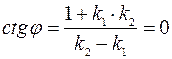 , откуда
, откуда 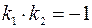 . Справедливо и обратное утверждение.
. Справедливо и обратное утверждение.
Пример. Составить уравнение прямой 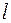 , проходящей через точку
, проходящей через точку 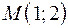 и перпендикулярной прямой
и перпендикулярной прямой 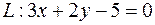 .
.
Решение. Перепишем общее уравнение прямой 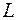 в виде уравнения прямой с угловым коэффициентом
в виде уравнения прямой с угловым коэффициентом 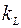 :
:
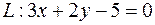 ,
, 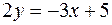 ,
, 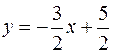 , значит
, значит 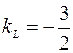 .
.
Прямые 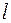 и
и 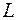 перпендикулярны по условию, значит
перпендикулярны по условию, значит 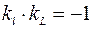 , следовательно,
, следовательно, 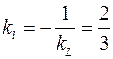 .
.
Подставляя в уравнение (3.5) 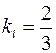 ,
, 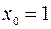 ,
, 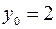 находим искомое уравнение прямой
находим искомое уравнение прямой 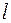 :
:
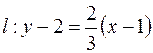
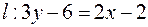
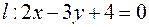
Ответ: 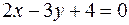 .
.
 2015-03-22
2015-03-22 429
429








