Уравнение Шредингера для кристалла

Из квантовой механики известно поведение электронов в изолированном атоме: энергетический спектр электронов имеет дискретный характер, переходы с одного энергетического уровня на другой связаны с поглощением или излучением энергии.

При конденсации изолированных атомов в кристалл, в котором они находятся на расстояниях порядка размера атома, кроме взаимодействия с ядром и электронами собственного атома каждый электрон испытывает действие других электронов и ядер кристалла. Волновые функции электронов перекрываются, что приводит к расщеплению энергетических уровней и превращению их в энергетические зоны (рис. 4.1).

В результате перекрывания волновых функций электроны получают возможность переходить от одного атома к другому за очень короткое время; другими словами, происходит обобществление электронов. В большей мере это относится к валентным электронам; волновые функции электронов внутренних оболочек атомов перекрываются незначительно, поэтому определяющим их энергетическое состояние фактором является взаимодействие с собственным ядром.

Энергетический спектр электронов в кристалле носит дискретный характер, однако, расстояние между соседними уровнями оказывается настолько малым, что в пределах энергетической зоны изменение энергии можно считать непрерывным. Определение зависимости энергии электрона в кристалле от волнового вектора, то есть установление закона дисперсии 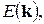и является главной задачей зонной теории.

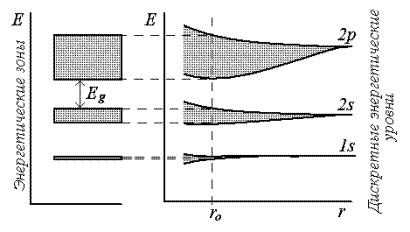Рис. 4.1. Расщепление энергетических уровней атомов при уменьшении расстояния между ними

Кристалл представляет собой совокупность большого числа атомных ядер и электронов. Решение задачи о стационарных состояниях и энергетическом спектре такой системы может быть найдено из решения стационарного уравнения Шредингера

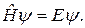(4.8)

Для кристалла 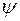является функцией координат всех электронов 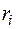и атомных ядер 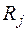, а оператор Гамильтона[5] имеет вид

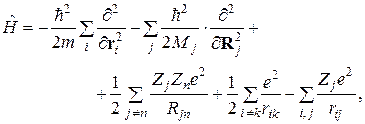(4.9)

где 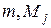– массы электронов и ядер; 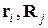– радиус-векторы і-го электрона и j-го ядра; 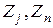– атомные номера ядер; 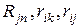– расстояния между соответствующими ядрами и электронами.

Первое слагаемое в (4.9) описывает кинетическую энергию электронов, второе – кинетическую энергию ядер, следующие слагаемые учитывают потенциальные энергии взаимодействия ядер друг с другом, электронов друг с другом и ядер с электронами. Решить задачу в таком виде невозможно из-за большого числа независимых переменных. Поэтому прибегают к упрощениям.

Первое из них заключается в делении системы частиц на две подсистемы – легких электронов и тяжелых ядер. Можно считать, что в состояниях наиболее вероятных, то есть с минимумом свободной энергии, кинетические энергии электронов и ядер одного порядка, а, следовательно, скорости электронов должны быть на два порядка выше, чем скорости ядер. Поэтому для какой-нибудь, даже неравновесной, конфигурации ядер электроны практически безынерционно будут приходить в равновесие между собой. За время, необходимое для изменения состояния электронов, состояние ядер остается практически неизменным, поэтому систему электронов и систему ядер можно считать независимыми. Другими словами, кристалл представляет собой систему, которая состоит из двух независимых подсистем, практически не обменивающихся энергией. Такое приближение называется адиабатическим. В этом приближении волновую функцию системы можно представить в виде произведения двух волновых функций, одна из которых описывает состояние электронов, а другая ядер

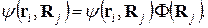(4.10)

При подстановке (4.10) в (4.8) последнее разделяется на два уравнения, одно из которых описывает движение электронов

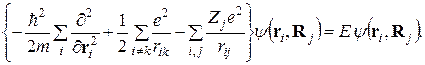(4.11)

Координаты ядер 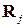входят в это уравнение как постоянные параметры. При таком подходе теряется описание некоторых явлений (поляронное состояние, сверхпроводимость и др.), но, к сожалению, не устраняются главные трудности задачи: она остается проблемой многих тел.

Второе приближение заключается в переходе к одноэлектронной задаче. Для этого действие всех электронов на данный электрон заменяют некоторым усредненным полем и многоэлектронную волновую функцию представляют в виде произведения одноэлектронных функций

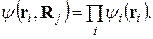(4.12)

При такой подстановке уравнение (4.11) распадается на независимые, одинаковые для каждого электрона уравнения

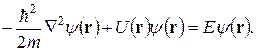(4.13)

Здесь 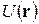— периодическое поле, создаваемое ионами кристаллической решетки и всеми другими электронами, кроме рассматриваемого. Определение конкретного вида поля и вызывает наибольшие трудности. При использовании одноэлектронного приближения теряются некоторые явления, связанные с коррелированным движением электронов, например, дырочная проводимость.

В зависимости от вида потенциального поля и степени локализации электронов возможны три основных подхода к решению одноэлектронного уравнения Шредингера (4.13): приближение свободных электронов, приближение сильно связанных и приближение слабо связанных электронов.

В первом случае потенциал решетки предполагается постоянным в пространстве, то есть не учитывается периодичность кристалла. Во втором случае потенциальная энергия представляется периодической функцией с периодом, равным периоду решетки, но на каждом периоде мало отличающимся от потенциальной энергии электрона в изолированном атоме. Такой подход справедлив для электронов внутренних оболочек. Если потенциальная энергия является периодической функцией и по величине сравнима с кинетической энергией электрона, то можно использовать приближение слабо связанных электронов.

Волна Блоха [6] и квазиимпульс электрона. Теорема Блоха утверждает, что волновую функцию электрона в периодическом поле можно представить в наиболее общем виде

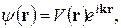(4.14)

где 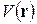имеет такую же периодичность, как и поле кристаллической решетки.

Из общих физических соображений ясно, что состояние электрона характеризуется импульсом, который сохраняется, тогда, когда электрон перемещается в постоянном поле. В этом случае состояние электрона не изменяется при смещении его на любой, сколь угодно малый вектор. Поскольку пространство кристаллической решетки, в котором движется электрон, не является однородным, то блоховская волновая функция существенно отличается от волновой функции свободного электрона. Однако, ввиду периодичности решетки, состояние электрона не изменяется при перемещении на вектор трансляции 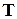, и поэтому вектор 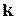, который входит в (4.14), называется квазиволновым вектором. Соответственно вектор 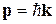называется квазиимпульсом, причем он имеет некоторые свойства обычного импульса. Главное его отличие заключается в неоднозначности.

Преобразование параллельного переноса 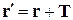умножает блоховскую функцию на 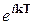. Следовательно, определенному состоянию электрона можно сопоставить не только вектор 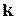, но и любой другой вектор

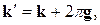(4.15)

где 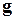есть произвольный вектор обратной решетки

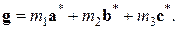(4.16)

здесь 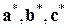– основные трансляции обратной решетки, 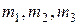– произвольные целые числа.

При параллельном переносе заме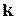на на 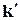просто приводит к умножению блоховской волновой функции на единицу, потому что из определения обратной решетки следует

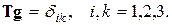(4.17)

Таким образом, квазиимпульс является неоднозначным вектором, определенным с точностью до произвольного вектора обратной решетки, умноженного на 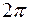. Физически разные значения вектора 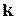находятся в пределах одной элементарной ячейки обратной решетки.

4.3. Модель Кронига [7] – Пенни [8]

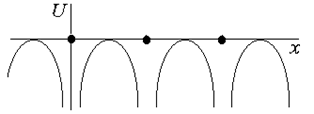
Для того чтобы найти характер зависимости энергии электрона в кристалле от волнового вектора или, другими словами, установить закон дисперсии, рассмотрим одномерную модель – линейную цепочку атомов, потенциальное поле которой имеет периодический характер (рис. 4.2, а). Отыскать решение уравнения Шредингера для такого потенциала затруднительно, поэтому заменим действительную форму потенциальной ямы на прямоугольную (рис.4.2, б). Хотя такой потенциал существенно отличается от действительного, однако он сохраняет главную особенность – периодичность.

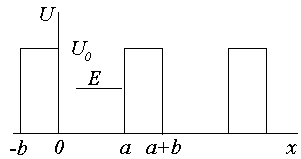а	б
Рис. 4.2. Потенциальное поле одномерного кристалла – линейной цепочки атомов (а) и потенциал Кронига-Пенни (б)

Уравнение Шредингера для электрона с энергией 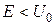имеет решения

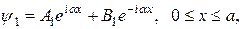(4.18)

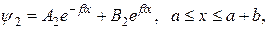
где 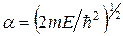и 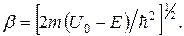(4.19)

В силу периодичности поля решения можно представить также в виде волны Блоха

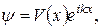(4.20)

где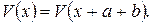

Из (4.18) и (4.20) следует

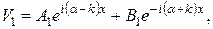(4.21)

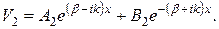
Потребуем выполнение условий непрерывности для функции 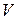и ее производной в точках 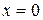и 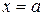, кроме того, условия периодичности 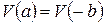. Это приведет к системе из четырех уравнений

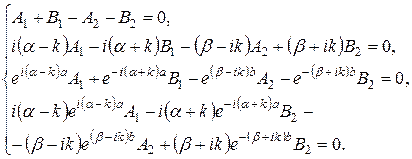(4.22)

Условием существования нетривиального решения однородной системы (4.22) является равенство нулю ее определителя. Выписывая и раскрывая определитель системы, получаем

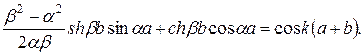(4.23)

Из (4.23) следует, что энергия электрона является неоднозначной функцией волнового числа 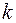. Для выяснения этой зависимости упростим задачу, заменив барьеры прямоугольной формы 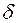-образными. Для этого одновременно устремим 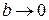и 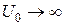таким образом, чтобы 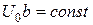. В этом случае прозрачность барьера мало изменяется, а уравнение (4.23) существенно упрощается

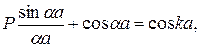(4.24)

где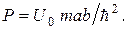

Выражение (4.24) называется уравнением Кронига-Пенни. Из него следует, что энергия является неоднозначной функцией 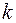. Для установления характера этой зависимости проведем графоаналитическое решение уравнения (4.24). Левую часть выражения (4.24) представим в виде функции от 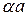(рис.4.3). Так как 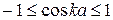для действительных значений 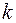, возможные значения 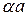ограничиваются некоторыми вполне определенными областями. Другими словами, решения для незатухающих волн имеются только для определенных разрешенных энергетических зон (зачерненные участки оси 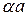на рис. 4.3).

Ширина разрешенных зон увеличивается с ростом энергии (или 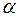) и уменьшается при увеличении 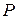. Параметр 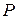характеризует «мощность» потенциальных барьеров, которые разделяют области с нулевым потенциалом. Если 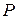постоянное, а энергия электрона растет, то последнему легче «просочиться» через барьер, и когда 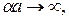электрон ведет себя как свободный.

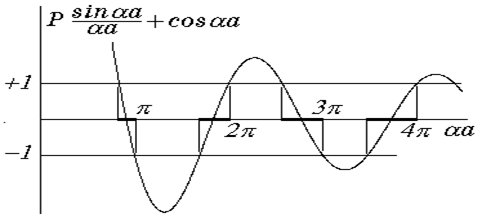Рис.4.3. К модели Кронига-Пенни

При увеличении 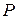ширина разрешенной энергетической зоны уменьшается и при 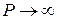разрешенными оказываются только значения 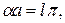где 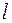— целое число. Эти решения просто описывают энергетические уровни частицы в бесконечно глубокой потенциальной яме.

Оба предельных случая имеют аналоги в реальных кристаллах – приближение свободных электронов и приближение сильное связанных электронов.

Энергетический спектр электрона, который отвечает решению уравнения (4.24), изображен на рис.4.4. Самая нижняя разрешенная энергетическая зона относительно наиболее узка, с увеличением энергии 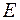ширина разрешенных зон растет, а запрещенных – уменьшается.

Зоны Бриллюэна. Для первой области разрешенных энергий 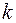изменяется в границах от 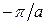до 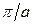. Этот интервал называется первой зоной Бриллюэна. Вторая зона располагается симметрично относительно первой и начала координат и включает участк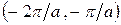и и 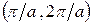, третья зона – 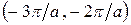и 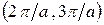и т.д. Суммарный интервал, который отвечает зоне Бриллюэна какого-либо номера, всегда равняется .

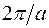Понятие зоны Бриллюэна распространяется и на случаи двух и трехмерных решеток.

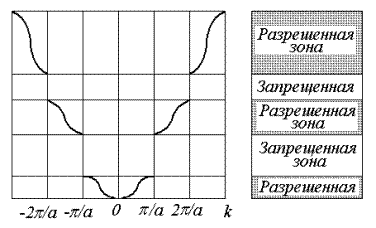Рис.4.4. Закон дисперсии для электрона в модели Кронига - Пенни

В общем случае зоной Бриллюэна называется область 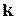- пространства, в пределах которой энергия изменяется непрерывно, а на границах терпит разрыв. В случае трехмерных решеток зоны Бриллюэна можно определить непосредственно из уравнения Брэггов, записанного в форме

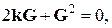(4.25)

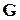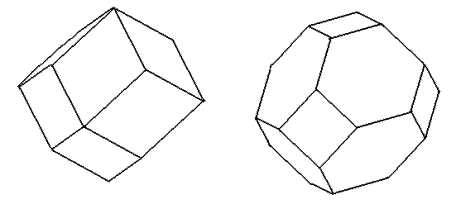
где – вектор обратной решетки, умноженный на 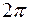. Примеры первой зоны Бриллюэна для кубических решеток приведены на рис. 4.5.

В большинстве случаев можно ограничиться рассмотрением первой зоны Бриллюэна, поскольку волновой вектор 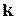может быть всегда сведен к вектору 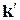лежащему в первой зоне, вычитанием или добавлением некоторого вектора обратной решетки, умноженного на 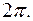Операция построения энергетических зон в пределах первой зоны Бриллюэна называется приведением зон к первой зоне, а сами такие зоны называются приведенными.

а б

Рис. 4.5. Первые зоны Бриллюэна для объемноцентрированной (а) и гранецентрированной (б) кубической решетки

На рис. 4.6 показаны приведенные зоны, причем у всех нечетных зон в центре располагаются минимумы, а на границах – максимумы энергии.

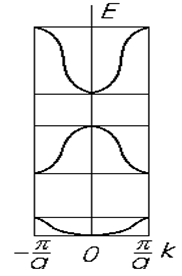Рис. 4.6. Приведенные зоны

На границах зоны энергия терпит разрыв. Условие разрыва 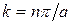(где 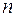–целое) можно представить в другом виде, воспользовавшись тем, что 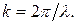В этом случае 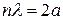, что является условием брэгговского отражения при нулевом угле падения. Движение электронов сквозь решетку кристалла можно рассматривать как распространение дебройлевских электронных волн, которые имеют вид бегущих волн. Когда выполняется брэгговское условие, появляется отражение, и вместо бегущей волны наблюдается стоячая. При этом возникают области запрещенных значений энергии.

Число уровней в зоне. Линейная цепочка, которая имеет ограниченную длину 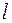, содержит конечное число элементарных ячеек 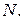Чтобы подсчитать число возможных состояний, ведем периодические граничные условия для волновых функций 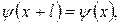полагая длину блока периодичности равной длине цепочки. Тогда волновой вектор электрона в первой зоне Бриллюэна будет принимать следующий набор значений:

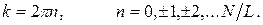(4.26)

Значение 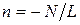из этого набора исключено, потому что оно не является независимым. Следовательно, полное число значений 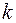равняется числу элементарных ячеек 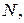а это значит, что каждая элементарная ячейка дает одно независимое значение 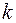в каждую энергетическую зону. Это утверждение справедливо и для трехмерного кристалла.

Так как каждый электрон может иметь одну из двух спиновых ориентаций, число независимых состояний в каждой энергетической зоне будет равняться 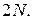При ширине зоны порядка электронвольта и числе состояний порядка 10²² (для кристалла объемом 1 см³) расстояние между уровнями в зоне будет порядка 10^-22 эВ.