Функции одной независимой переменной не охватывают все зависимости, существующие в природе. Многим явлениям возникающим, в том числе в технике, естествознании и экономике, свойственна многофакторная зависимость. Исследование таких зависимостей потребовало совершенствование математического аппарата, в частности, введения понятия функции нескольких переменных.
Примерами функций двух и нескольких переменных могут служить:
Ø площадь 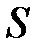 прямоугольника со сторонами
прямоугольника со сторонами 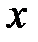 и
и 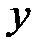 , выражаемая формулой
, выражаемая формулой 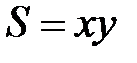 , т.е. значения
, т.е. значения 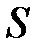 определяются совокупностью значений
определяются совокупностью значений 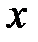 и
и 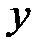 ;
;
Ø Объем 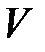 прямоугольного параллелепипеда с ребрами
прямоугольного параллелепипеда с ребрами 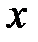 ,
, 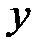 и
и 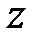 , выражается формулой
, выражается формулой 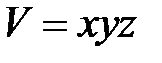 , т.е. значения V зависят от трех переменных.
, т.е. значения V зависят от трех переменных.
Ø закон Ома, который гласит, что 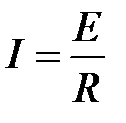 , где I – сила тока, Е – электродвижущая сила, и R – сопротивление, т.е. значения I – определяются совокупностью значений Е и R;
, где I – сила тока, Е – электродвижущая сила, и R – сопротивление, т.е. значения I – определяются совокупностью значений Е и R;
Ø абсолютная температура 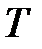 , давление
, давление 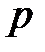 и объем
и объем 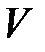 данной массы газа связаны формулой Менделеева – Клайперона
данной массы газа связаны формулой Менделеева – Клайперона 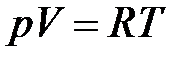 , где
, где 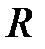 - некоторая постоянная. Отсюда, например,
- некоторая постоянная. Отсюда, например, 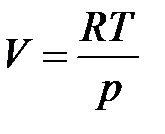 , т.е. значения
, т.е. значения 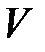 зависят от значений
зависят от значений 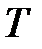 и
и 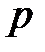 ;
;
Ø функция Кобба – Дугласа – производственная функция, показывающая объем выпуска продукции Y при затратах капитала К и трудовых ресурсов L. Для случая двух переменных она имеет вид 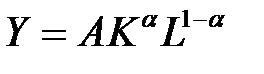 , где
, где 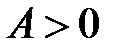 – параметр производительности конкретно взятой технологии,
– параметр производительности конкретно взятой технологии, 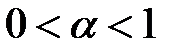 – доля капитала в доходе.
– доля капитала в доходе.
Ø Понятие функции полезности является одним из базовых в экономической теории. В широком смысле она выражает зависимость полезности, т.е. результата, эффекта некоторого действия от уровня (интенсивности) этого действия. Многомерным ее аналогом является функция 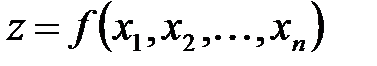 , которая выражает полезность от
, которая выражает полезность от 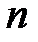 приобретенных товаров.
приобретенных товаров.
Чаще всего встречаются следующие ее виды:
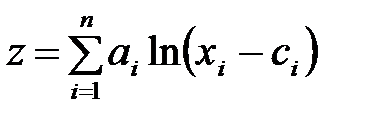 , где
, где 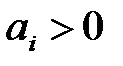 ,
, 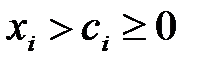 ;
;
б) функция постоянной эластичности
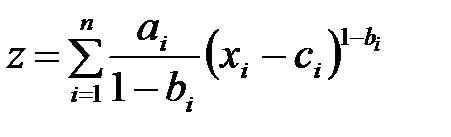 , где
, где 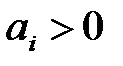 ,
, 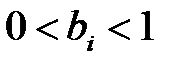 ,
, 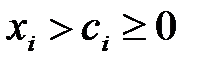 .
.
Для изучения подобного рода зависимостей вводится понятие функций двух и нескольких переменных.
 2015-03-07
2015-03-07 1000
1000







