Вихревое электрическое поле

Второе уравнение Максвелла представляет собой закон электромагнитной индукции. Максвелл высказал гипотезу, что всякое переменное магнитное поле возбуждает в окружающем пространстве электрическое поле, которое и является причиной возникновения индукционного тока в проводящем контуре. Изменяющееся во времени магнитное поле 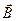порождает вихревое электрическое поле 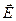, циркуляция которого вдоль произвольного замкнутого контур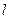а равна

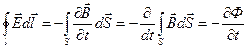, (16.6)

где магнитный поток

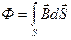. (16.7)

Согласно представлениям Максвелла, контур, в котором появляется ЭДС индукции, играет второстепенную роль, являясь своего рода лишь «прибором», обнаруживающим это поле.

На основании теоремы Стокса

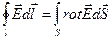, (16.8)

получим из (16.6)

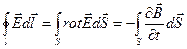, или 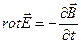. (16.9)

Соотношение (16.9) является вторым уравнением Максвелла в дифференциальной форме: вихрь вектора 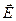пропорционален скорости изменения вектора .

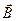16d:\Program Files\Physicon\Open Physics 2.5 part 1\content\chapter1\section\paragraph2\theory.htmld:\Program Files\Physicon\Open Physics 2.5 part 1\design\images\ring_h.gif.3. Третье и четвертое уравнения Максвелла

Третье уравнений Максвелла в интегральной форме

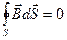(16.10)

выражает тот факт, что в природе отсутствуют магнитные заряды, т.е. все силовые линии вектора 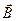являются замкнутыми линиями.

Воспользуемся известной из векторного анализа теоремой Гаусса

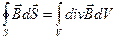(16.11)

и запишем третье уравнение Максвелла в виде

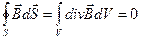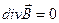, . (16.12)

Уравнение (16.12) называется третьим уравнением Максвелла в дифференциальной форме.

Наконец, воспользуемся теоремой Остроградского-Гаусса (10.12), которое и является четвертым уравнением Максвелла

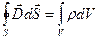, (16.13)

где 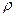- объемная плотность свободных зарядов.

Сутьчетвертого уравнения состоит в том, что поток вектора электрического смещения 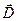через произвольную замкнутую поверхность 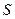равен алгебраической сумме свободных зарядов, расположенных внутри этой поверхности.

Поскольку в природе существуют как положительные, так и отрицательные электрические заряды, то силовые линии вектора 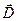не являются замкнутыми линиями. Они начинаются на положительных зарядах и заканчиваются на отрицательных зарядах.

Применив к уравнению (16.13) теорему Гаусса (16.11), запишем четвертое уравнение Максвелла в дифференциальной форме:

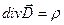. (16.14)

Полная система уравнений Максвелла в дифференциальной форме

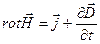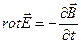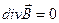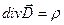, , , . (16.15)

Отметим, что в уравнениях Максвелла (1873 г.) заложено существование электромагнитных волн. Согласно уравнениям Максвелла, всякое переменное магнитное поле возбуждает в окру­жающем пространстве вихревое электрическое поле, а всякое переменное электрическое поле вызывает появление вихревого магнитного поля. Возбуждение взаимосвязанных электрического и магнитного полей и есть электромагнитная волна. Экспериментальное подтверждение гениальных предсказаний Максвелла было осуществлено в опытах Герца в 1888 г.

Векторы полей, входящие в уравнения Максвелла, не являются независимыми. Между ними существует определенная связь:

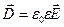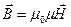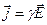, , , (16.16)

где 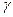- удельная проводимость вещества.

Эти уравнения называются материальными уравнениями.

Контрольные вопросы

1. Что является причиной возникновения вихревого электрического поля? Чем оно отличается от электростатического поля?

2. Чему равна циркуляция вихревого электрического поля?

3. Что такое ток смещения?

4. Выведите выражение для плотности тока смещения.

5. Запишите теорему о циркуляции вектора напряженности магнитного поля, объяснив ее физический смысл.

6. Запишите полную систему уравнений Максвелла в интегральной форме и объясните их физический смысл.

7. Запишите полную систему уравнений Максвелла в дифференциальной форме и объясните их физический смысл.

8. Какие основные выводы можно сделать на основе теории Максвелла?