Для заданной выборки из генеральной совокупности СВ Х (n =100, представлены ниже таблицами 1–30), по своему варианту необходимо:
1. Определить размах варьирования значений случайной величины и составить вариационный ряд распределения;
2. По формуле Стерджеса определить длину интервалов и составить интервальный вариационный ряд;
3. Найти выборочную среднюю 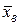 , выборочную дисперсию
, выборочную дисперсию 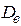 , выборочное среднее квадратическое отклонение
, выборочное среднее квадратическое отклонение 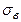 , моду М 0, медиану М е и коэффициент вариации
, моду М 0, медиану М е и коэффициент вариации 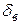 ;
;
4. Построить эмпирическую функцию распределения вероятностей F *(x).
5. Построить гистограмму относительных частот и линию эмпирической плотности;
6. Пользуясь критерием Пирсона проверить гипотезу о нормальном законе распределения генеральной совокупности при уровне значимости α=0,05, предварительно вычислив для каждого интервала группирования вариационного ряда выравнивающие частоты;
7. На гистограмме относительных частот нанести линию теоретической плотности f (x) нормального распределения;
8. Найти доверительный интервал для оценки неизвестного математического ожидания генеральной совокупности случайной величины с надежностью γ=0,95.
|
|
|
| 11.1 | |||||||||||||||
| 11.2 | |||||||||||||||
| 11.3 | |||||||||||||||
| 11.4 | |||||||||||||||
| 11.5 | |||||||||||||||
| 11.6 | |||||||||||||||
| 11.7 | |||||||||||||||
| 11.8 | |||||||||||||||
| 11.9 | |||||||||||||||
| 11.10 | |||||||||||||||
| 11.11 | |||||||||||||||
| 11.12 | |||||||||||||||
| 11.13 | |||||||||||||||
| 11.14 | |||||||||||||||
| 11.15 | |||||||||||||||
| 11.16 | |||||||||||||||
| 11.17 | |||||||||||||||
| 11.18 | |||||||||||||||
| 11.19 | |||||||||||||||
| 11.20 | |||||||||||||||
| 11.21 | |||||||||||||||
| 11.22 | |||||||||||||||
| 11.23 | |||||||||||||||
| 11.24 | |||||||||||||||
| 11.25 | |||||||||||||||
| 11.26 | |||||||||||||||
| 11.27 | |||||||||||||||
| 11.28 | |||||||||||||||
| 11.29 | |||||||||||||||
| 11.30 | |||||||||||||||
|
|
|
|
|
|
|
|
|
 2015-03-07
2015-03-07 1135
1135








