Промежуточные модели идеализированных материалов

Модель	Вид модели	Графики течения	Уравнение	Условные обозначения
Гука		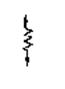θ	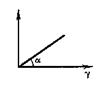θ = γG σ = ε Е	θ, σ – касательное и нормальное напряжения, Па; γ, ε – угловая и линейная деформации; G, Е – модули упругости при угловой и линейной деформации
Ньютона		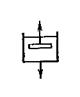θ	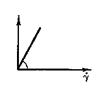θ = ηγ*	γ* – скорость сдвига, с-1; η – вязкость при сдвиге, Па·с;
Сен-Венана		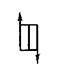θ	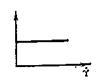При θ < θТ нет деформации, при θ = θТ течение	θТ – предел текучести при сдвиге, Па

При объемном сжатии напряжения и деформации связаны посредством объемного модуля упругости К (в Па):

σ = Кε_v, (1.18)

где ε_v вычисляется по зависимости (1-8), модуль объемной упругости – по выражению:

К = Е / 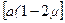, (1.18 а)

Объемный модуль упругости при одноосном деформировании тела в замкнутом объеме, а = 1, при трехосном деформировании с приложением одинаковых напряжений, а = 3 может быть вычислен также по формуле:

К = ЕG /(Е + G), (1.18 б)

Для описания упругих свойств продуктов в различных зонах деформирования часто недостаточно классических понятий о модулях упругости. Тогда можно применить модификации модулей упругости: условно-мгновенный, эластический и др.

Упругие свойства определяются предельным напряжением сдвига и другими механическими характеристиками.

Идеальновязкая жидкость характеризуется тем, что в ней напряжения пропорциональны скорости деформации.

θ = η γ^*, (1.19)

где η – коэффициент вязкости; γ^* - скорость сдвига.

Вязкое течение происходит под действием любых сил, как бы малы они ни были, однако скорость деформации при уменьшении сил снижается, а при их исчезновении обращается в нуль. Для таких жидкостей вязкость, являющаяся константой, пропорциональна напряжению сдвига.

Закон Ньютона описывает поведение многих низкомолекулярных жидкостей при сдвиге и продольном течении (воды, маловязких жидкостей с неразветвляющимися молекулами). Модель вязкого течения – Ньютонова тела в виде поршня с отверстиями показана в табл. 1.3.

Механическая модель ньютоновской жидкости представляет собой демпфер, состоящий из поршня, который перемещается в цилиндре с жидкостью. При перемещении поршня жидкость через зазоры между поршнем и цилиндром протекает из одной части цилиндра в другую. При этом сопротивление перемещению поршня пропорционально его скорости.

Полная вязкость движущейся жидкости складывается из ламинарной (ньютоновской), турбулентной и объемной вязкости.

Идеальнопластическое тело Сен-Венана может быть представлено в виде элемента, состоящего из двух прижатых друг к другу пластин. При относительном перемещении пластин между ними возникает постоянная сила трения, не зависящая от нормальной силы. Тело по Сен-Венану не начнет двигаться до тех пор, пока напряжение сдвига не превысит некоторого критического значения – предела текучести (предельного напряжения сдвига), после чего элемент может двигаться с любой скоростью.

Модель этого, Сен-Венанова, тела в виде пары трения скольжения показана в табл. 1.3.

Модели, имеющие малое число элементов, редко дают удовлетворительную сходимость опытных данных с рассчитанными по уравнениям. Увеличение количества элементов сверх четырех не приводит к существенному качественному изменению модели, так как модели, содержащие до четырех элементов включительно, исчерпывают все разнообразие механического поведения данного материала.

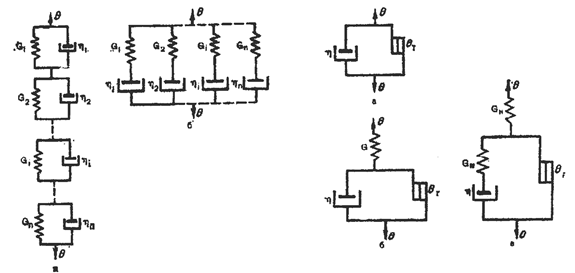
Для того, чтобы описать реологическое поведение сложного тела в зависимости от свойств его компонентов, можно комбинировать в различных сочетаниях рассмотренные выше модели простейших идеальных тел, каждое из которых обладает лишь одним физико-механическим свойством. Эти элементы могут быть скомбинированы параллельно или последовательно.

Основными сложными моделями являются: упруго-пластическое тело; вязко-упругие тела Кельвина-Фойгта и Максвелла; вязко-пластические тела Бингама, Шведова и Шведова-Бингама.

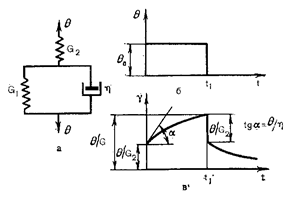
Модель упруго-пластического тела получается при последовательном соединении упругого элемента Гука с модулем упругости G и пластического элемента Сен-Венана с пределом текучести θ_Т (рис. 1.4). При θ< θ_Т происходит упругая деформация материала, при θ = θ_Т – пластическое течение.

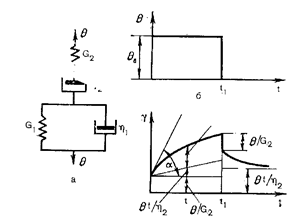
Вязко-упругое тело Кельвина-Фойгта представлено механической моделью, полученной при паралеллельном соединении упругого элемента Гука с модулем упругости G и вязкого элемента Ньютона с вязкостью η (рис. 1.5) Под действием растягивающего усилия пружина удлиняется, а поршень будет двигаться в жидкости. Движение поршня связано с вязким сопротивлением жидкости, ввиду чего полное растяжение пружины наступает не сразу. Когда нагрузка устранена, пружина сжимается до первоначальной длины, но это требует времени вследствие вязкого сопротивления жидкости.

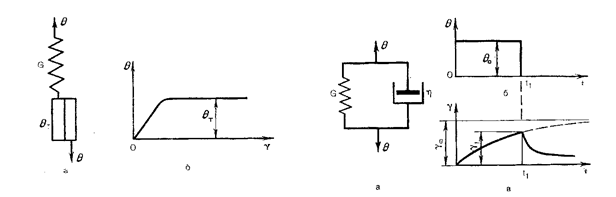
Рис. 1.4 Модель упруго-пластического тела (а) и диаграмма θ – γ (б)

Рис. 1.5 Модель Кельвина-Фойгта (а) и диаграммы θ-t (б), γ-t (в)

Модель тела по Кельвину отражает явление упругого последействия, которое представляет собой изменение упругой деформации во времени, когда она или постоянно нарастает до некоторого предела после приложения нагрузки, или постепенно уменьшается после ее снятия.

Механическая модель упруго-вязкого релаксирующего тела по Максвеллу – это последовательно соединенные элементы Гука с модулем упругости G и Ньютона с вязкостью η (рис. 1.6).

На оба элемента действует одинаковое напряжение θ. Тело по Максвеллу ведет себя как упругое или как вязкое в зависимости от отношения времени релаксации к длительности эксперимента. Итак, если под действием мгновенного усилия пружина растягивается, а затем сразу нагрузка снята, то поршень не успевает двигаться и система ведет себя как упругое тело.

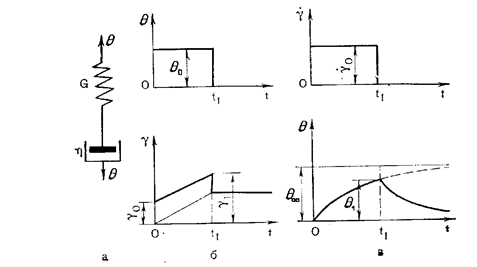
Рис. 1.6 Модель Максвелла (а) и диаграммы θ - t, γ - t, γ^* - t при постоянных напряжении (б) и

скорости деформации (в)

Однако, с другой стороны, если, поддерживать растяжение пружины постоянным, она постепенно релаксирует, перемещая поршень вверх, и система ведет себя почти как ньютоновская жидкость.

Рис. 1.7 Обобщенные модели Кельвина (а) и Максвелла (б)

Рис. 1.8 Вязко-пластические модели: а – Шведова-Бингама; б – Бингама; в - Шведова

Обобщенные механические модели Кельвина и Максвелла (рис. 1.7) сочетают в себе свойства вязкости и упругости, так что их деформация под действием напряжения определяется как сумма m составляющих элементов соответственно тела Кельвина Фойгта и тела Максвелла.

Двухэлементная механическая модель вязко-пластического тела Шведова-Бингама (рис. 1.8, а) состоит из соединенных параллельно элементов Ньютона с вязкостью η и Сен-Венана с пределом текучести θ_Т.

Модель вязко-пластического тела по Шведову-Бингаму характеризует материалы, которые в первом приближении можно рассматривать как тела по Сен-Венану. Они начинают течь, когда напряжение сдвига достигнет предельного напряжения. Если нет вязкого сопротивления, то скорость течения материала станет сколь угодно большой. Во втором приближении такие материалы должны обладать еще вязкостью. Все это приводит к постулированию идеального тела Бингама, сочетающего упругость, вязкость и пластичность.

Механическая модель Бингама (рис. 1.8, б) состоит из элементов Гука с модулем упругости G, Ньютона с вязкостью η и Сен-Венана с пределом текучести θ_Т. Элементы Ньютона и Сен-Венана соединены взаимно параллельно, а вместе – последовательно с элементом Гука.

Под действием напряжения θ < θ_Т модель Бингама имеет только упругую деформацию. Реологическое уравнение этой модели при θ > θ_Т:

γ* = θ*/ G + (θ-θ_Т ) / η, (1.20)

Под действием напряжения θ < θ_Т модель Бингама имеет только упругую деформацию. Реологическое уравнение этой модели при θ > θ_Т:

γ* = θ* / G + (θ-θ_Т) / η, (1.20, а)

Механическая модель Шведова (рис. 1.8, в) состоит из элементов Гука с модулем упругости G_H, Сен-Венана с пределом текучести θ_Т и Максвелла с модулем упругости G_М и вязкостью η. При θ θ_Т деформация модели Шведова происходит только благодаря элементу Гука. При θ>θ_Т деформируются все элементы модели.

Реологическое уравнение модели Шведова в дифференциальной форме имеет вид:

γ^* = θ^* (1 / G_H + 1 / G_М) + (θ - θ_Т) / η, (1.21)

Модель тела по Шведову отличается от модели по Бингаму тем, что параллельно модели Сен-Венана присоединена модель Максвелла, а у модели Бингама – элемент Ньютона.

Рассмотрим еще две сложные модели, которые часто применяют при расчете деформации пищевых материалов. Это трехэлементная модель Максвелла-Томсона и четырехэлементная модель Бюргерса.

Модель Максвелла-Томсона представляет собой модель Кельвина-Фойгта, к которой последовательно присоединен упругий элемент Гука (рис. 1.9). Эту модель часто называют моделью стандартного вязко-упругого тела.

Модель Бюргерса состоит из последовательно соединенных моделей Кельвина-Фойгта и Максвелла (рис. 1.10).

Рис. 1.9 Модель Максвелла-Томсона (а) и диаграммы θ - t (б) и γ – t (в)	Рис. 1.10 Модель Бюргерса (а) и диаграммы θ - t (б) и γ – t (в)

Как было показано, все механические модели, являясь абстрактными, состоят из простейших элементов (пружины, поршня, твердого блока) и позволяют наглядно представить мгновенную, запаздывающую и вязкую деформации, внешнее трение и релаксацию напряжений в исследованном сырье, полуфабрикатах и готовых изделиях. Это трудно установить из дифференциальных уравнений, описывающих деформационное поведение материалов.

Следует подчеркнуть, что механическое моделирование процесса деформирования пищевого материала в условиях, наиболее приближенных к реальным, позволит использовать его структурно-механические характеристики при описании течения среды в механических устройствах, а также моделировать технологические процессы с целью их оптимизации.

Моделирование деформационного поведения пищевых материалов можно проводить на основе не только механических моделей, но и электрических. При этом механическое напряжение сопоставляют с э.д.с. электрической цепи, скорость деформации – с электрическим током, модуль упругости – с обратной величиной емкости, а вязкость – с сопротивлением. Последовательное соединение элементов механической модели эквивалентно параллельному соединению элементов электрической цепи, а параллельное механической модели – последовательному соединению в электрической. Электрическое моделирование позволяет применять моделирующие ЭВМ при изучении упруго-вязко-пластических свойств пищевых материалов, а также при расчете процессов их переработки.

1.4 Основные уравнения напряжений и деформаций «идеальных»
и сложных реальных тел

Структурно-механические свойства характеризуют поведение продукта в условиях напряженного состояния и позволяют связать между собой напряжения, деформации или скорости деформаций в процессе приложения усилий. Они не являются «чистыми» константами материала и существенно зависят от формы и размеров тела, скорости нагружения, состояния поверхности, влияния окружающей среды, температуры, структуры и множества других факторов.

Для описания механического поведения различных деформируемых и текучих систем используют «идеальные» модели (рис. 1.4), которые обычно дают линейные кривые деформирования. Кроме того, на практике часто встречаются нелинейно пластично-вязкие материалы, течение которых описывается полуэмпирическими и эмпирическими моделями. Следует также иметь в виду, что одноосное сжатие и сдвиг (течение) часто описываются формально одинаковыми уравнениями. Процесс деформации более сложных реологических тел можно характеризовать составными моделями, которые включают в той или иной комбинации простейшие элементы: упругость, пластичность, вязкость. Количество таких комбинаций практически неограниченно.

Комбинируя три основные модели (по Гуку, по Сен-Венану, по Ньютону), можно получить уравнения напряжений и деформаций для различных реальных тел. Однако полученные уравнения, часто имея линейный характер, недостаточно точно описывают течение и деформирование пищевых продуктов.

Процесс деформации более сложных реологических тел можно описать уравнениями, полученными при рассмотрении общего напряженного или деформационного состояния.

Линейные уравнения напряжений и деформаций для моделей, представленных в табл. 1.3 широко используются для описания деформационного поведения пищевых продуктов, как при сдвиговых, так и при нормальных напряжениях.

Процессы в релаксирующей жидкообразной среде (Максвеллова вязко-упругая жидкость), когда вызванные внешним воздействием деформации полностью исчезают во времени (рис. 1.6), описываются уравнением Максвелла. Под действием напряжения θ в теле возникает деформация γ, имеющая во времени определенную скорость γ^* = dγ/dτ, которая складывается из упругой γ_упр и вязкой γ*_вяз составляющих. Упругую составляющую находят дифференцированием по времени закона Гука:

(dγ /dτ)_УПР = dθ / (Gdτ) = θ*/G, (1.22)

Вязкую составляющую определяют из уравнения Ньютона:

(d γ /dτ)_ВЯЗ = θ /η, (1.22, а)

Суммируя две составляющие, получают уравнение Максвелла:

dγ /dτ = dθ / (Gdτ) + θ / η, ηγ^* = ηθ* / G+θ, (1.23)

которое можно проинтегрировать для частных случаев.

Если предположить, что деформация постоянна, т.е. γ* = 0, то можно наблюдать процесс рассасывания, релаксации напряжений, причем при τ = 0 напряжение равно какому-то начальному значению θ = θ₁. При интегрировании в пределах от θ₁ до θ и от 0 до τ получают уравнение:

θ = θ₁ ехр (- Gτ / η), (1.24)

называемое экспоненциальным законом релаксации напряжений. Если в этом уравнении η/G обозначить через τ_р, то оно примет вид:

θ = θ₁ ехр (- τ /τ_Р), (1.25)

где τ_Р - период релаксации, с.

Период релаксации характеризует быстроту процесса, т.е. перехода системы из неравновесного термодинамического состояния, вызванного внешним воздействием, в состояние термодинамического равновесия. За это время напряжение убывает в 2,7 раза.

В многофазной реальной системе может протекать одновременно несколько процессов с различными периодами релаксации. После завершения процессов с наименьшим периодом наступает неполное статическое равновесие. Поведение тела можно описать кривой распределения периодов релаксаций.

При сложении упругих и вязких напряжений по методу Фойгта-Кельвина (рис. 1.5) получают уравнение для упруго-вязкой твердообразной среды:

θ = γG + ηdγ /dτ, или θ = G , (1.26)

При снятии напряжения (θ = 0) и интегрировании в пределах от γ_max до γ и от 0 до τ получают экспоненциальную функцию для релаксации деформации:

γ = γ_max exp (- Gτ / η), или γ = γ_max exp (-τ / τ_р), (1.27)

Если среду, подчиняющуюся уравнению Фойгта-Кельвина, нагрузить постоянным напряжением θ₂ при τ >0, то интегрирование дает:

γ = (θ₂ / G) [1-exp (-τ / τ_р)], (1.27, а)

т.е. деформация во времени постепенно увеличивается, стремясь к значению γ = θ₂ /G при τ .

Комбинация уравнений для моделей Максвелла и Фойгта – Кельвина, выполненная произвольным приравниванием правых частей уравнений 1.23 и 1.26, приводит к математической зависимости для модели стандартного линейного тела.

θ + τ_γ θ^* = G_R (γ + τ_θ γ*), (1.28)

где G_R - релаксационный модуль упругости, определяемый соотношением между упругими и пластичными характеристиками продукта, Па; τ_γ - период релаксации напряжения при постоянной деформации, с; τ_θ - период релаксации деформации при постоянном напряжении, с.

При сложении напряжений, соответствующих пластическому и вязкому течениям (рис. 1.8), получают уравнение Шведова-Бингама для пластично-вязкой среды:

θ = θ₀ + ηdγ /dτ, (1.29)

Это уравнение неоднократно использовали для описания деформационного поведения многих пищевых продуктов.

Простейшим случаем пластичного твердого тела является тело Бингама. При нагрузке ниже предела текучести (θ<θ₀) оно ведет себя как гуковское тело (θ = Gγ), выше (θ 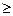θ₀) – как жидкость (θ = η_плγ + θ₀). Такие деформационные свойства наблюдаются у сливочного масла при t 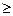4 ⁰С, плавленых сыров и сыров типа чеддер.

Входящая в эти уравнения величина периода релаксации имеет большое значение при исследовании физико-механических свойств, особенно при малых напряжениях и времени действия напряжения того же порядка, как период релаксации. В зависимости от периода релаксации деформации тела можно разделить на два рода. Когда продолжительность действия силы меньше периода релаксации, энергия, подводимая к системе, вызывает упругие деформации по всему объему. Когда продолжительность действия силы больше периода релаксации, процесс протекает с накоплением энергии и влечет за собой остаточные деформации.

Из уравнений релаксации видно, что при бесконечном времени после разгрузки тела напряжения или деформации полностью релаксируют. Однако, для рассматриваемых тиксотропных систем напряжения обычно не релаксируют до нуля. Поэтому Д.С. Великовский считает, что процессы старения, которые являются следствием коагуляции и упрочнения структурной сетки в результате слипания близко расположенных частиц, увеличивают прочность структурного каркаса во времени. Длительное измерение развития процесса релаксации невозможно, так как конечные условия не будут соответствовать начальным.

Таким образом, течение реальных твердых тел наблюдается после превышения критического напряжения – предела текучести. При дальнейшем нагружении достигается предел прочности, при превышении которого твердое тело разрушается. Это явление наблюдается в таких процессах, как дробление или резание. И поэтому имеет технологическое значение. Если разрушение происходит без существенного изменения формы – говорят о хрупком разрушении. Если разрушению предшествует значительное изменение формы – говорят о вязком разрушении.

Закон деформирования модели Максвелла-Томсона (рис. 1.9) можно записать в следующем виде.

θ + Т_Р θ* = Gγ + Т_Р G₂γ*, (1.30)

где G - длительный модуль упругости, Па; G₂ – мгновенный модуль упругости, Па; Т_Р- время релаксации, с;

Т_Р = η /(G₁ + G₂); G = G₁G₂/ (G₁ + G₂), (1.31)

Уравнение изменения деформации при ползучести тела Максвелла-Томсона имеет вид:

γ = θ / G₂ + θ (1/ G₂ – 1 / G) е ^{– G t /G 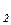Т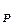} , (1.32)

Для случая релаксации напряжений при γ = γ₀ = const уравнение 1.30 принимает вид:

θ + Т_Р θ* = Gγ₀, (1.33)

Из этого уравнения при начальном напряжении θ = θ₀ получим:

θ = Gγ₀ +(θ₀- Gγ₀) е ^{–t /Т}_р, (1.34)

Выражение 1.34 показывает, что при t 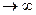напряжение стремится к постоянной величине Gγ₀, что соответствует процессу релаксации пищевых материалов.

Уравнение ползучести модели Бюргерса (рис. 1.10.) имеет вид:

γ = θ / G₂ + θt / η₂ + (θ/G₁) [1- е ^{–G 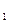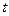/ η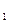} ], (1.35)

Нелинейные эмпирические уравнения напряжений и деформаций. Реологические модели не всегда позволяют достаточно точно описать кривую деформации или течения продуктов. В этом случае приходится пользоваться различными эмпирическими и полуэмпирическими уравнениями. При этом они могут содержать несколько (3-5) констант, определяемых из опыта, что делает их ненадежными и сложными для практического использования. Значимость этих уравнений также оценивается по-разному. Для описания течения различных пищевых материалов чаще других применяются два основных уравнения, ряд других можно получить из них в виде частных случаев.

Уравнение Шульмана:

(θ^1/а - θ 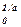)^b = ηγ*, (1.36)

где а, b – экспериментально определяемые коэффициенты; при а = b = 2 это уравнение превращается в уравнение Кэссона:

θ^1/2 = а₀ + а₁γ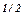^* , (1.36, а)

Уравнение Гершеля – Балкли:

θ – θ₀ = В₁^*γ^{* n}, (1.37)

где В₁^* – коэффициент, пропорциональный вязкости при градиенте скорости, равном единице, Па·сⁿ; n – индекс течения, характеризующий угол наклона линии течения в логарифмических шкалах.

При θ₀ = 0 уравнение приобретает вид степенного уравнения Оствальда де Вале:

θ = В₁^*γ^*n, (1.37, а)

где В 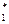- коэффициент, пропорциональный вязкости при градиенте скорости, равном единице, Па сⁿ; n – индекс течения.

При n = 1 – Шведова-Бингама, тогда В₁^* представляет собой пластическую вязкость.

Таким образом, приведенные математические зависимости позволяют описать поведение пищевых продуктов в различных условиях деформирования при приложении нормальных и касательных напряжений.

Наибольшее применение получили реологические уравнения Оствальда (степенной закон), Бингама и Балкли-Гершеля, которые математически достаточно просты и имеют минимальное количество параметров.

Получить реологические уравнения, учитывающие все компоненты деформации пищевых материалов, практически невозможно. Однако, если модель наиболее полно учитывает условия деформации, то ее реологическое уравнение отражает особенности поведения материала и им можно пользоваться в инженерных расчетах.