Задачи Дирихле в конце для уравнения Лапласа

Пусть требуется решить задачу Дирихле для уравнения Лапласа.

Δ U = 0 в области, заключенной между 2-мя концентрическими окружностями L ₁ и L ₂ радиусов R ₁и R ₂ с центрами в начале координат

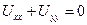
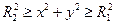
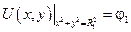
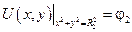
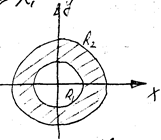
U (x, y) – гармоническая, т.е. Δ U = 0 для любой 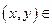кольцу.

U (x, y) на L ₁ и L ₂ принимает заданные значения.

Перейдем к полярным координатам

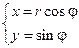
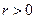
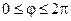
Как известно, уравнение Лапласа в полярных координатах имеет вид

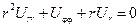
Задачи Дирихле в померных координатах:

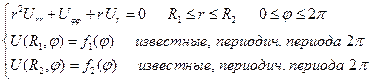
Решим поставленную задачу методом Фурье, будет искать решение в виде:

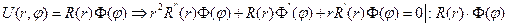
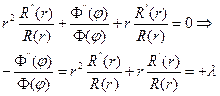
Про это уравнение говорят, что в нем переменные разделены т.к. левая часть зависит только от 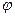, правая – от r. Тогда поскольку r и 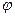не зависят друг от друга, то каждая часть уравнения должна быть const.

Тогда получаем 2-е задачи:

1.

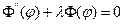
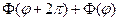
2.

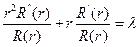
1-я задача была решена.

Было показано, что решение

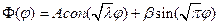и неревиальное решение только при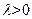

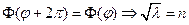, где n – целое 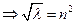- собственные значения и соответств. им собственные функции

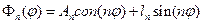
n=…-1,-0,1,2,…

Найдем функцию :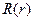

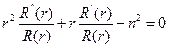
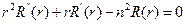
Если 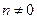, то решение имеем в виде:

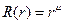, то есть нужно найти число μ, при котором функция r^μ удовлетворяет этому уравнению

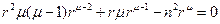
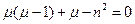
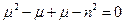
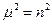
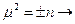Если 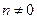, то функци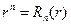и

и 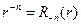- собственные функции поставленной задачи.

Если 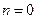, то

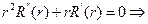
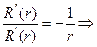
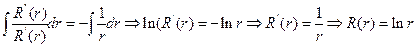- собственная функция задачи 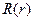при нулевом значении n.

Таким образом при 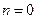исходное дифференциальное уравнение имеет 2-а решения:

1. Тривиальное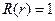

2. Нетривиальное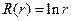

Есть бесконечный ряд собственных функций исходной задачи

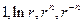
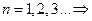
Собственные функции задачи на нахождение :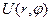

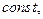
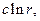
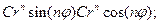
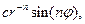
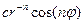
Тогда общее решение будет иметь вид:

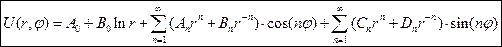
Общее решение задачи Дирихле для кольца

А₀, B₀, A_n, B_n, C_n, D_n n=1,2,3,4…

const находится из граничных условий

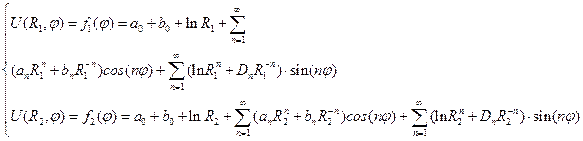
1-ое уравнение – ряд Фурье функции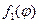

2-ое уравнение – ряд Фурье функции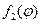

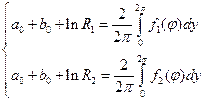Находим: a₀,b₀

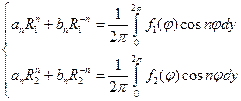Находим: a_n,b_n

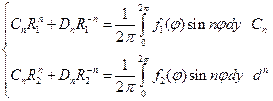
Следовательно решение задачи Дирихле в кольце записывается в виде указанного в рамочке е коэффициента (a₀,b₀, a_n,b_n, c_n,d_n вычисляем. по этим 3-м системам

Из найденного решения в кольце можно