10. Дифференциал и его геометрический смысл
Рассмотрим функцию 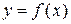 , которая определена и непрерывна в точке
, которая определена и непрерывна в точке  и некоторой ее окрестности и дифференцируема в точке
и некоторой ее окрестности и дифференцируема в точке  .
.
Функция дифференцируема, следовательно, существует ее производная
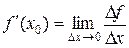 .
.
По теореме 1 § 11 имеем:
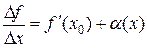 ,
,
где 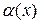 – б/м функция при
– б/м функция при  , следовательно,
, следовательно,
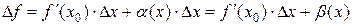 ,
,
где 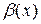 – б/м функция при
– б/м функция при  (
(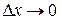 ), большего порядка малости, чем
), большего порядка малости, чем 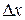 . Таким образом, получили:
. Таким образом, получили:
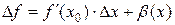 . (1)
. (1)
Рассмотрим:
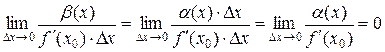 ,
,
следовательно, функция 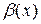 сильнее стремится к нулю. Основной вклад в разложение (1) делает первое слагаемое.
сильнее стремится к нулю. Основной вклад в разложение (1) делает первое слагаемое.
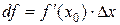 – главная часть разложения приращения функции по
– главная часть разложения приращения функции по 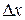 .
.
Пусть приращение функции представимо в виде:
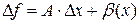 , (2)
, (2)
где 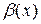 – б/м функция при
– б/м функция при  (
(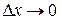 ), большего порядка малости, чем
), большего порядка малости, чем 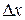 . Покажем, что функция
. Покажем, что функция  в этом случае дифференцируема. Действительно:
в этом случае дифференцируема. Действительно:
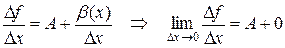
(т.к. 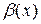 стремится к нулю быстрее, чем
стремится к нулю быстрее, чем 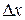 ), следовательно, существует производная
), следовательно, существует производная
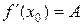 .
.
Если функция представима в виде (2), то говорят, что функция дифференцируема.
Определение. Дифференциалом функции называется величина, пропорциональная бесконечно малому приращению аргумента 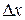 и отличающаяся от соответствующего приращения функции на бесконечно малую величину более высокого порядка чем
и отличающаяся от соответствующего приращения функции на бесконечно малую величину более высокого порядка чем 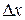 .
.
Дифференциал функции 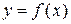 обозначается через
обозначается через 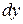 или
или 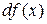 .
.
Необходимым и достаточным условием существования дифференциала функции 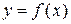 в точке
в точке  служит существование ее производной в этой точке, и тогда
служит существование ее производной в этой точке, и тогда
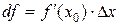 .
.
Определение. Приращение 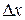 независимой переменой
независимой переменой  называют ее дифференциалом
называют ее дифференциалом 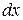 , т.е.
, т.е.
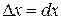 .
.
Таким образом,
Дифференциал функции равен ее производной, умноженной на дифференциал независимой переменной, т.е.
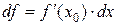 .
.
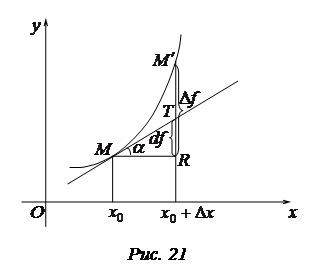
Рассмотрим геометрическую иллюстрацию дифференциала функции 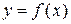 (рис. 21). Т.к.
(рис. 21). Т.к. 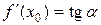 , то дифференциал
, то дифференциал 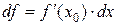 измеряет отрезок
измеряет отрезок 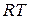 .
.
 Дифференциал
Дифференциал 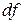 функции
функции 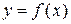 в точке
в точке  численно равен приращению ординаты касательной, построенной к графику функции в точке
численно равен приращению ординаты касательной, построенной к графику функции в точке 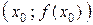 , соответствующему изменению аргумента
, соответствующему изменению аргумента  от значения
от значения  до значения
до значения 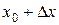 .
.
Приращение функции 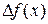 изображается приращением ординаты точки линии (отрезок
изображается приращением ординаты точки линии (отрезок 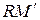 ). Поэтому разность между дифференциалом и приращением изображается отрезком
). Поэтому разность между дифференциалом и приращением изображается отрезком 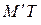 , заключенным между линией и касательной к ней; длина этого отрезка является при
, заключенным между линией и касательной к ней; длина этого отрезка является при 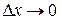 бесконечно малой величиной более высокого порядка, чем длина отрезка
бесконечно малой величиной более высокого порядка, чем длина отрезка  .
.
20. Свойства дифференциала функции
1) 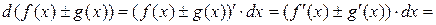
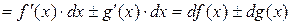 .
.
Таким образом,
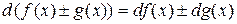 .
.
2) 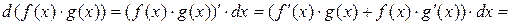
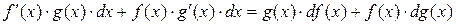 .
.
Таким образом,
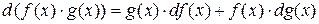 .
.
3) 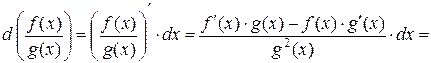
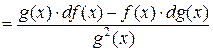 .
.
Таким образом,
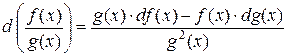 .
.
30. Дифференциал сложной функции. Свойство инвариантности
Рассмотрим свойство дифференциала функции, вытекающее из правила дифференциала сложной функции.
Пусть 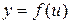 и
и 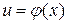 – непрерывные функции своих аргументов, имеющие производные по этим аргументам
– непрерывные функции своих аргументов, имеющие производные по этим аргументам 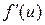 и
и 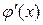 . Если обозначить
. Если обозначить 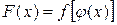 , то
, то 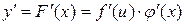 . Умножая обе части уравнения на
. Умножая обе части уравнения на 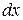 , получим:
, получим:
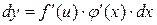 ,
,
но 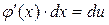 , и значит,
, и значит,
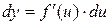 ,
,
т.е. дифференциал 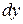 имеет такой же вид, как если бы величина
имеет такой же вид, как если бы величина 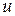 была бы независимой переменной.
была бы независимой переменной.
Дифференциал функции 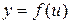 сохраняет одно и то же выражение, независимо от того, является ли ее аргумент
сохраняет одно и то же выражение, независимо от того, является ли ее аргумент 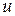 независимой переменной или функцией от независимой переменной.
независимой переменной или функцией от независимой переменной.
Это свойство называется инвариантностью (т.е. неизменностью) формы дифференциала.
40. Приближенное вычисление с помощью дифференциала
Пусть в точке  производная функции
производная функции 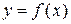 отлична от нуля:
отлична от нуля: 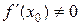 . Тогда
. Тогда
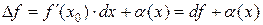 ,
,
где 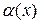 – б/м величина при
– б/м величина при 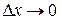 более высокого порядка, чем
более высокого порядка, чем 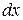 .Но при указанном условии она будет б/м величиной более высокого порядка и чем
.Но при указанном условии она будет б/м величиной более высокого порядка и чем 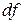 и
и 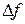 . Действительно, при
. Действительно, при 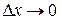 имеем:
имеем:
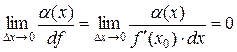 ,
,
ибо 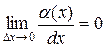 , а
, а 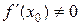 . Значит,
. Значит, 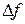 и
и 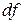 отличаются друг от друга на бесконечно малую величину более высокого порядка, чем они сами, и, следовательно, они эквивалентны:
отличаются друг от друга на бесконечно малую величину более высокого порядка, чем они сами, и, следовательно, они эквивалентны:
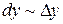 .
.
Отсюда получаем приближенную формулу вычисления:
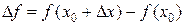 ,
, 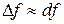 , следовательно,
, следовательно,
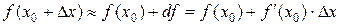 . (3)
. (3)
Формула (3) называется формулой приближенного вычисления с помощью дифференциала.
Пример 1. Вычислить приближенно 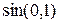 .
.
Решение. Имеем: 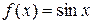 ,
, 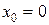 ,
, 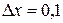 . Тогда:
. Тогда:
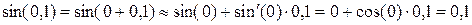 .
.
Пример 2. Вычислить приближенно 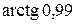 .
.
Решение. Имеем: 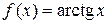 ,
, 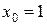 ,
, 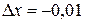 . Тогда:
. Тогда:
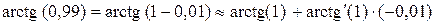 .
.
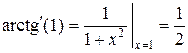 ,
, 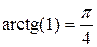 , следовательно,
, следовательно,
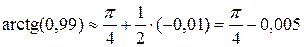 .
.
50. Дифференциалы высших порядков
Пусть дана дифференцируемая функция 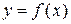 . Тогда
. Тогда 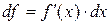 .
.
Определение. Дифференциалом второго порядка функции  называется дифференциал от функции
называется дифференциал от функции 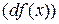 :
: 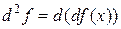 .
.
Аналогично:
Дифференциалом 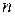 -го порядка называется дифференциал от дифференциала
-го порядка называется дифференциал от дифференциала 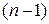 -го порядка как функции
-го порядка как функции  :
: 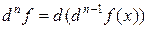 .
.
Найдем выражение второго дифференциала функции 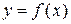 . Т.к.
. Т.к. 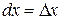 не зависит от
не зависит от  , то при дифференцировании считаем
, то при дифференцировании считаем 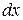 постоянным:
постоянным:
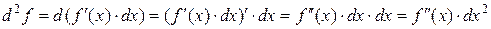 .
.
Аналогично: 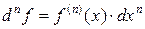 .
.
Отсюда находим, что 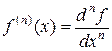 .
.
 2015-02-14
2015-02-14 9751
9751
