1. Сформировать выборку из 10 случайных чисел, лежащих в диапазоне от 0 до 1.
2. Сформировать выборку из 20 случайных чисел, лежащих в диапазоне от 5 до 20.
3. Пусть спортсмену необходимо составить график тренировок на 10 дней, так чтобы дистанция, пробегаемая каждый день, случайным образом менялась от 5 до 10 км.
4. Составить расписание внеклассных мероприятий на неделю для случайного проведения: семинаров, интеллектуальных игр, КВН и спец. курса.
5. Составить расписание на месяц для случайной демонстрации на телевидении одного из четырех рекламных роликов турфирмы. Причем вероятность появления рекламного ролика №1 должна быть в два раза выше, чем остальных рекламных роликов.
| Лабораторная работа №3 |
| Применение инструментальных средств для решения основных задач математической статистики (вариант будет разобран на лабораторной) |
1) по результатам методики СПА (К.Роджерс, Р.Даймонд), проанализируйте особенности социально-психологической адаптации студентов 1-го курса обучения; 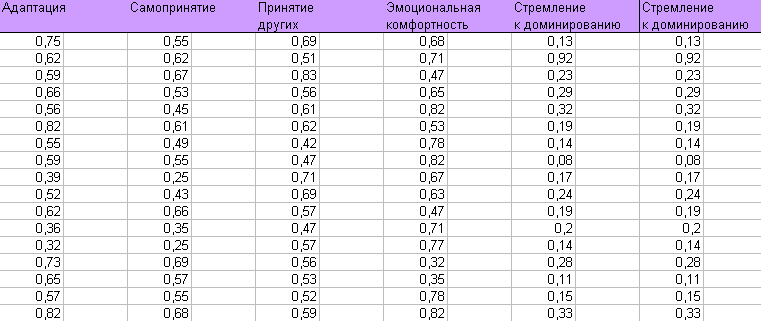 2) постройте гистограмму распределения для параметра "Адаптация" и, исходя из полученных данных, дайте характеристику выборке по данному параметру. 2) постройте гистограмму распределения для параметра "Адаптация" и, исходя из полученных данных, дайте характеристику выборке по данному параметру. |
| Лабораторная работа №4 |
| Алгоритмы параметрических критериев. Критерий Стьюдента. Критерий Фишера. В решении задач обязательно должны быть: 1)Условие задачи. 2)Формулировка гипотез. 3)Решение задачи. 4)Вывод. |
Задача №1 Детям давались обычные арифметические задания, после чего одной случайно выбранной половине учащихся сообщали, что они не выдержали испытания, а остальным обратное. Затем, у каждого ребенка спрашивали, сколько секунд ему бы потребовалось для решения аналогичной задачи. Экспериментатор вычислял разность между называемым ребенком в временем (x1) и результатом выполненного задания (x2). Ожидалось, что сообщение о неудаче вызовет некоторую неадекватность самооценки ребенка. Проверяемая гипотеза (на уровне a=0.05) состояла в том, что дисперсия совокупности самооценок не зависит от сообщений об удаче или неудаче. 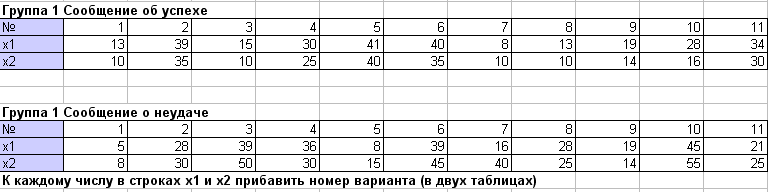 |
| Задача №2 Исследовалось влияние условий воспитания в детском доме детей на интеллектуальное развитие детей. При использовании стандартного теста интеллекта были получены следующие данные (N=36) 91, 96, 99, 108, 108, 122, 101, 96, 125, 82, 116, 102, 92, 112, 84, 102, 121, 109, 107, 115, 93, 113, 113, 103, 82, 120, 90, 107, 102, 104, 110, 121, 112, 97, 121,89. (Для каждого числа прибавить номер варианта V).Исследователя интересовало, превышает ли интеллект воспитанников детского дома нормативный показатель А=100+V-2. Для принятия статистического решения уровень a=0.05. |
| Задача №3 Имеются 2 выборки по объектам исследования 1)104; 103,5; 104; 102; 104; 103,5; 103,5; 104; 103. 2)104; 102; 103; 103; 103; 102; 102; 102; 103; 102; 101,5; 102;101. (Для каждого числа прибавить номер варианта V).Предположив, что соответствующие генеральные совокупности имеют нормальное распределение, необходимо установить наличие различий в уровнях средних значений исследуемого признака при уровне значимости а=0,05. |
Задача №4 На группе из 8 рабочих изучалось время выполнения одних и тех же технологических операций (в мин.): X- время выполнения операции в 1-ый раз. Y- время выполнения операции после 3-х повторов. Установить, зависит ли время выполнения операций от количества их повторений. Исходные данные: 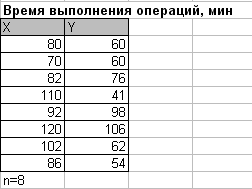 (Для каждого числа прибавить номер варианта V). (Для каждого числа прибавить номер варианта V). |
Задача №5 В 2-х группах по 11 объектов исследования в каждой, изучались различия по некоторому признаку. Измеренные значения признака в первой и второй группах в таблице: 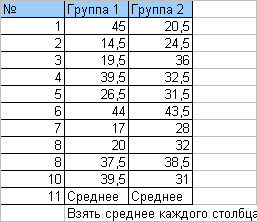 Необходимо проверить наличие различий по выборкам используя критерий Фишера. (Для каждого числа прибавить номер варианта V). Необходимо проверить наличие различий по выборкам используя критерий Фишера. (Для каждого числа прибавить номер варианта V). |
| Лабораторная работа №5 |
| Проверка гипотезы о нормальном распределении генеральной совокупности по критерию Пирсона (Пример решения задачи) |
1)Используя критерий Пирсона, при уровне значимости 0,05 проверить, согласуется ли гипотеза о нормальном рампределении генеральной совокупности Х с эампирическим распределением выборки: V - номер варианта. 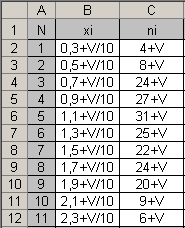 2)Используя критерий Пирсона, при уровне значимости 0,05 проверить, согласуется ли гипотеза о нормальном рампределении генеральной совокупности Х с эампирическим распределением выборки: 2)Используя критерий Пирсона, при уровне значимости 0,05 проверить, согласуется ли гипотеза о нормальном рампределении генеральной совокупности Х с эампирическим распределением выборки: 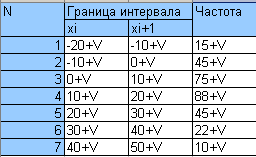 V - номер варианта. Таблицы значений функции f(x) и F(x) V - номер варианта. Таблицы значений функции f(x) и F(x) |
Вычисления можно проводить в Excel.
| Лабораторная работа №6 |
| Выявление различий в уровне исследуемого признака. Q-критерий Розенбаума, U-критерий Манна-Уитни, H-критерий Крускала-Уолиса, S-критерий тенденций Джонкира. (К каждому числу прибавлять номер варианта) |
| Задача 1. |
В группе слушателей ФПК по педагогике и психологии назрел глухой конфликт между иногородними слушателями и слушателями, проживавшими в Санкт-Петербурге, где и происходили занятия. В курсе психологического практикума по групповой психологии иногородним слушателям было предложено принять на себя роль петербуржцев и участвовать в споре на их стороне. 8 слушателей были протагонистами -активными игроками, перевоплотившимися в петербуржцев, а 8 других суфлировали им, подсказывая реплики и ссылки на те или иные факты. После этого сеанса социодраматической замены ролей участникам был задан вопрос: "Если принять за 100% психологическую дистанцию между Вами и петербуржцами до дискуссии, то на сколько процентов она сократилась или увеличилась после дискуссии?" Результаты представлены в таблице. Все показатели имеют отрицательный знак, что свидетельствует о сокращении дистанции (Сидоренко Е. В., 1992). Могут ли эти данные использоваться как подтверждение идеи Д. Л. Морено о том, что принятие на себя роли оппонента способствует сближению с ним (Moreno G. L., 1934)? Показатели сокращения психологической дистанции (в %) после социодраматической замены ролей в группе протагонистов (n1=8)ч суфлеров (n2=8)  V-номер варианта (V<15) Значения 8-ой строки округлить. V-номер варианта (V<15) Значения 8-ой строки округлить. |
| Задача 2. |
В исследовании С.К. Скаковского (1990) изучалась проблема психологических барьеров при обращении в службу знакомств у мужчин и женщин. В эксперименте участвовали 19 мужчин и 25 женщины в возрасте от 17 до 45 лет (средний возраст 32,5 года). Испытуемые Должны были отметить на отрезке точку, соответствующую интенсивности внутреннего сопротивления, которое им пришлось преодолеть, чтобы обратиться в службу знакомств. Длина отрезка, отражающая максимально возможное сопротивление, составляла 100 мм. В Табл. приведены показатели интенсивности сопротивления, выраженные в миллиметрах. Можно ли утверждать, что мужчинам приходится преодолевать субъективно более мощное сопротивление? Показатели интенсивности внутреннего сопротивления при обращении в службу знакомств (в мм) 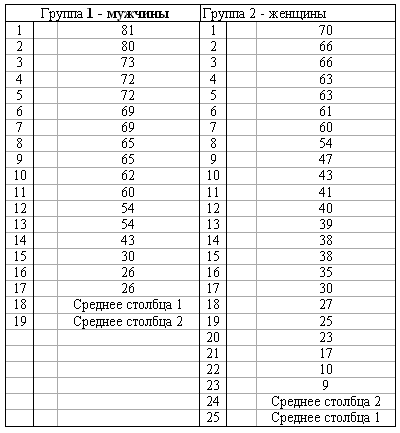 К каждому числу прибавить номер варианта (V<15) Значения средних округлить. К каждому числу прибавить номер варианта (V<15) Значения средних округлить. |
| Задача 3. (Джонкира, Крускала-Уоллиса) |
В выборке из 32 мужчин-руководителей подразделений крупного промышленного предприятия Санкт-Петербурга перед началом курса тренинга партнерского общения проводилось обследование с помощью 16-факторного личностного опросника Р. Б. Кеттелла (форма А). В Табл. приведены индивидуальные значения испытуемых по фактору N, отражающему житейскую искушенность и проницательность. Данные представлены в "сырых" баллах и сгруппированы по четырем возрастным группам. Можно ли утверждать, что есть определенная тенденция изменения значений фактора N при переходе от группы к группе? Индивидуальное значение по фактору N 16PF в 4 возрастных группах руководителей (по данным Е. В. Сидоренко, 1987) 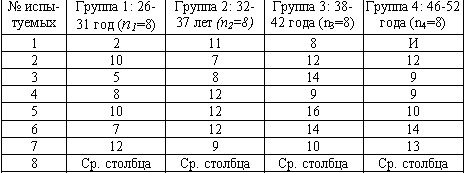 К каждому числу прибавить номер варианта (V<15) Значения средних округлить. К каждому числу прибавить номер варианта (V<15) Значения средних округлить. |
| Лабораторная работа №7 |
| Оценка достоверности сдвига в значениях исследуемого признака.G-критерий знаков. G-критерий Вилкоксона.Критерий Фридмана. L-критерий тенденций Пейджа. (К каждому числу прибавлять номер варианта) |
| Задача 1. |
Психолог провидит с младшими школьниками коррекционную работу по формированию навыков внимания, используя для оценки результатов корректурную пробу. Задача состоит в том, чтобы определить будет ли уменьшаться количество ошибок внимания у младших школьников после спец. коррекционных упражнений? (Критерий Вилкоксона)  V-номер варианта) Значения 20-ой и 21-ой строки округлить. V-номер варианта) Значения 20-ой и 21-ой строки округлить. |
| Задача 2. |
Шести школьникам предъявляют тест Равена. Фиксируется время решения каждого задания. Выясняется вопрос - будут ли найдены статистически значимые различия между временем решения первых трех заданий теста. (Критерий Фридмана)  К каждому числу прибавить номер варианта Значения средних округлить. К каждому числу прибавить номер варианта Значения средних округлить. |
| Задача 3. |
| Продолжая исследования, психолог решил проверить гипотезу. Действительно ли время решения задания увеличивается (от первой задачи к третьей) (Критерий Пейджа) Данные взять из второй задачи |
| Задача 4. |
Психолог проводит групповой тренинг. Его задача - выяснить, будет ли эффективен данный конкретный вариант тренинга для снижения уровня тревожности участников? (Критерий знаков) 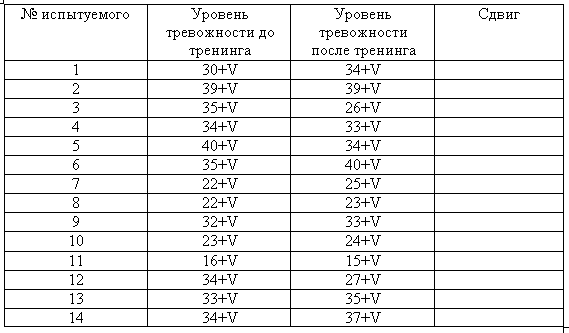 V-номер варианта) V-номер варианта) |
| Задача 5. |
Получив отрицательные результаты, психолог внес в способ тренинга соответствующие коррективы. И опять выдвинул гипотезу: улучшенный вариант тренинга позволяет эффективно снижать уровень тревожности испытуемых. (Критерий знаков)  (V-номер варианта) Средние - округлить. (V-номер варианта) Средние - округлить. |
[6] Решение математических задач средствами Excel: Практикум/ В.Я. Гельман. – СПб.: Питер, 2003 - с. 150-164
 2015-04-08
2015-04-08 4510
4510