Общая характеристика и особенности метода. Метод ЛКАО-МО. Двухуровневое приближение в квантовой механике.
Связывающее и разрыхляющее состояния.
В методе молекулярных орбиталей полная волновая функция молекулы строится из функций, характеризующих поведение отдельных электронов в поле, создаваемом остальными электронами и ядрами. В связи с этим молекулярная орбиталь представляет собой одноэлектронную волновую функцию, которая описывает поведение отдельного электрона в молекуле. Если атомная орбиталь является одноцентровой, то молекулярная орбиталь – многоцентровая. Это в свою очередь означает, что она «охватывает» несколько ядерных центров в молекуле. Аналогия между атомными и молекулярными орбиталями позволила перенести в метод молекулярных орбиталей основные положения теории атомных орбиталей многоэлектронного атома. Так, в методе молекулярных орбиталей состояние каждого электрона в молекуле описывается некоторой волновой функцией, которая называется молекулярной орбиталью. Каждой молекулярной орбитали соответствует определённая энергия, которая называется орбитальной энергией. Молекулярные орбитали заполняются электронами в соответствии с правилами, аналогичными правилам заполнения атомных орбиталей: принципом наименьшей энергии, принципом Паули и правилом Гунда. Интерпретация молекулярных орбиталей обусловлена вероятностной природой волновой функции. Так, если известна молекулярная орбиталь, то можно определить вероятность нахождения электрона в определённом объёме пространства. Электронная плотность даёт картину пространственного распределения электронного облака в молекуле. Графически молекулярные орбитали изображают с помощью граничной поверхности, ограничивающей область пространства, внутри которого содержится примерно 90% электронной плотности. Распределение электронов по молекулярным орбиталям в соответствии с правилами заполнения называют электронной конфигурацией молекулы. Расположение молекулярных орбиталей в порядке возрастания их энергий называют энергетической диаграммой. Молекулярные орбитали и соответствующие энергетические уровни обозначают одинаковыми символами. Уже при рассмотрении молекулярного иона водорода 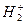 , впервые возникает важнейшее приближение в квантовой химии – метод ЛКАО – МО. Предположив, что межъядерное расстояние в ионе
, впервые возникает важнейшее приближение в квантовой химии – метод ЛКАО – МО. Предположив, что межъядерное расстояние в ионе 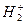 является бесконечно большим, можно переписать одноэлектронное уравнение Шрёдингера в виде двух уравнений, каждое из которых соответствует нахождению электрона или вблизи первого ядра, или вблизи второго:
является бесконечно большим, можно переписать одноэлектронное уравнение Шрёдингера в виде двух уравнений, каждое из которых соответствует нахождению электрона или вблизи первого ядра, или вблизи второго:
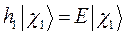
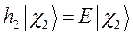
При этом гамильтонианы 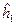 и
и 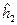 включают в себя кинетическую энергию электрона и потенциальную энергию притяжения электрона соответственно к первому и второму ядру:
включают в себя кинетическую энергию электрона и потенциальную энергию притяжения электрона соответственно к первому и второму ядру:
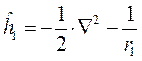
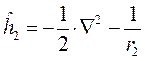
Очевидно, что в условиях, когда расстояние между ядрами бесконечно большое, они не взаимодействуют друг с другом, и волновые функции электрона 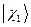 и
и 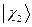 в уравнениях:
в уравнениях:
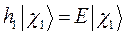
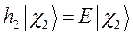
являются волновыми функциями атома водорода, т.е. 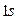 - атомными орбиталями:
- атомными орбиталями:
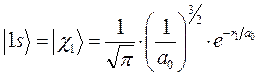
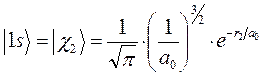
или в атомных единицах:
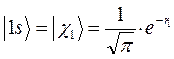
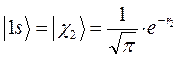
Очевидно, что атомным орбиталям 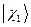 и
и 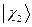 будет соответствовать одна и та же орбитальная энергия
будет соответствовать одна и та же орбитальная энергия 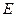 :
:
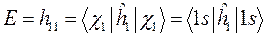
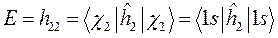
Поскольку некоторое событие (электрон находится в ионе 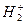 ) может быть представлено состоящим из нескольких более простых событий (электрон находится или вблизи первого ядра, или вблизи второго ядра), то на основании принципа суперпозиции, нетрудно увидеть, что молекулярная орбиталь такой системы (её полная волновая функция), может быть построена как линейная комбинация соответствующих атомных орбиталей, каждая из которых может быть описана своей волновой функцией; т.е. имеем соответственно:
) может быть представлено состоящим из нескольких более простых событий (электрон находится или вблизи первого ядра, или вблизи второго ядра), то на основании принципа суперпозиции, нетрудно увидеть, что молекулярная орбиталь такой системы (её полная волновая функция), может быть построена как линейная комбинация соответствующих атомных орбиталей, каждая из которых может быть описана своей волновой функцией; т.е. имеем соответственно:
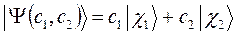
Это в свою очередь находится в полном соответствии с теоремой о невзаимодействии. Представление молекулярной орбитали в виде линейной комбинации атомных орбиталей, получило название приближения ЛКАО – МО. Здесь коэффициенты 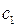 и
и 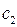 , определяют вклад соответствующих атомных орбиталей
, определяют вклад соответствующих атомных орбиталей 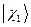 и
и 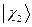 в общую молекулярную волновую функцию электрона
в общую молекулярную волновую функцию электрона 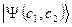 . Их называют орбитальными (вариационными) коэффициентами, или коэффициентами разложения. Легко заметить, что волновая функция в приближении ЛКАО – МО записывается аналогично пробной волновой функции
. Их называют орбитальными (вариационными) коэффициентами, или коэффициентами разложения. Легко заметить, что волновая функция в приближении ЛКАО – МО записывается аналогично пробной волновой функции 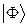 в вариационном методе Релея – Ритца. Следовательно, её можно определить вариационным методом, т.е. путём нахождения минимума полной энергии как функции параметров
в вариационном методе Релея – Ритца. Следовательно, её можно определить вариационным методом, т.е. путём нахождения минимума полной энергии как функции параметров 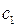 и
и 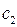 . В приближении ЛКАО – МО, молекулярную волновую функцию
. В приближении ЛКАО – МО, молекулярную волновую функцию 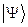 строят как линейную комбинацию некоторых базисных функций
строят как линейную комбинацию некоторых базисных функций 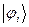 , записывая её в виде разложения:
, записывая её в виде разложения:
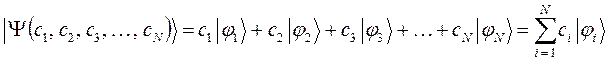
Реализация процедуры минимизации энергии приводит к выражениям для энергий и соответствующих им волновых функций симметричного и антисимметричного состояний квантово-механической системы. Для понимания физики явления, полезно рассмотреть самый простой случай вариационного метода, когда 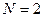 . Это значит, что пробная волновая функция
. Это значит, что пробная волновая функция 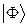 представляется в виде двух слагаемых:
представляется в виде двух слагаемых:
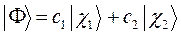
Базисные функции 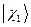 и
и 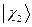 могут отвечать различным физическим ситуациям. Например,
могут отвечать различным физическим ситуациям. Например, 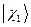 описывает движение электронов в некоторой области
описывает движение электронов в некоторой области 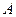 , а
, а 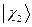 - в области
- в области 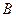 . На практике
. На практике 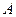 и
и 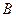 могут означать два разных атома, две области в молекуле и т.д. Такая модель называется двухуровневым приближением и часто используется в физике и квантовой химии. Так, по - определению имеем:
могут означать два разных атома, две области в молекуле и т.д. Такая модель называется двухуровневым приближением и часто используется в физике и квантовой химии. Так, по - определению имеем:
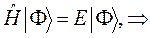
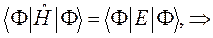
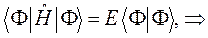
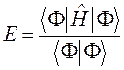
Подставляя в полученное уравнение для средней энергии разложение пробной волновой функции по базисному набору соответствующих базисных функций, будем иметь соответственно выражение:
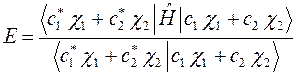
На основании теоремы о не взаимодействии, согласно которой «если система состоит из двух или нескольких невзаимодействующих подсистем, то её полная волновая функция 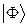 равна произведению волновых функций отдельных подсистем, а энергия – сумме энергий подсистем», а также учитывая, что:
равна произведению волновых функций отдельных подсистем, а энергия – сумме энергий подсистем», а также учитывая, что:
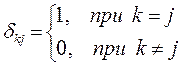
будем иметь соответственно после раскрытия скобок:
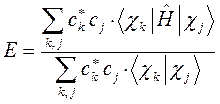
или для рассматриваемого случая:
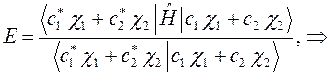
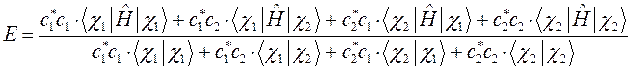
введём следующие обозначения:
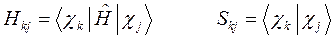
или для нашего случая:




с учётом введенных выше обозначений, выражение для средней энергии:
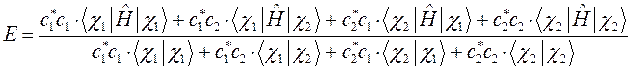
можно будет представить к виду:
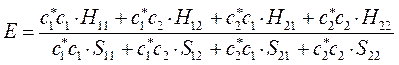
или в общем виде:
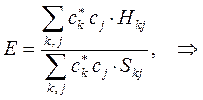
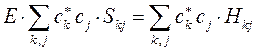
т.е. имеем соответственно:
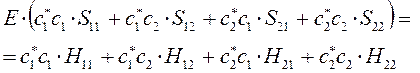
вариационные коэффициенты найдём из условия вида:
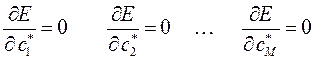
Дифференцируя полученное выражение (в общем виде) по коэффициенту 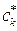 :
:
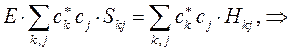
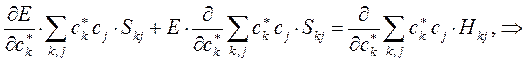
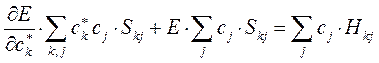
имеем для нашего случая:
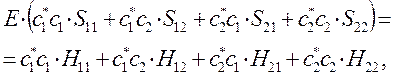
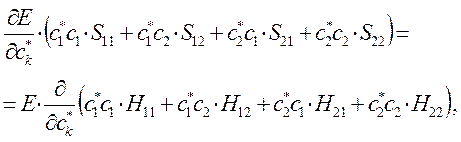
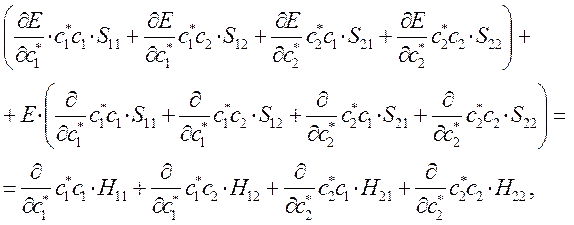
а так как производная от энергии по вариационному коэффициенту равна нулю в точке экстремума:
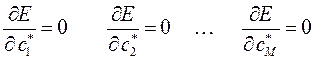
тогда:
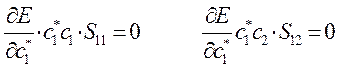
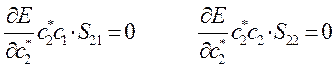
или в общем виде:
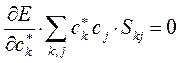
Полученное в ходе дифференцирования выражение:
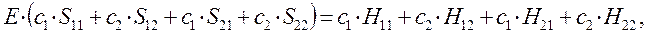
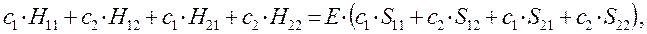
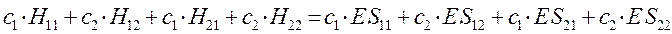
можно будет далее разделить на два линейных уравнения вида:
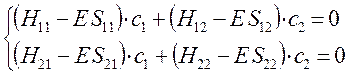
или в общем виде:
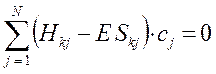
Полученная в ходе проделанных выше выкладок система уравнений, может быть далее задана в матричном виде:
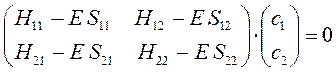
Данная система представляет собой систему линейных однородных уравнений. Из теории линейных уравнений известно, что такая система имеет нетривиальное решение при условии, что детерминант, составленный из коэффициентов при неизвестных (неизвестными являются вариационные коэффициенты), равен нулю:
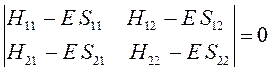
Учитывая свойство эрмитовости гамильтониана и ортонормированность базисных функций 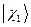 и
и 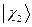 , будем иметь соответственно для диагональных и недиагональных элементов:
, будем иметь соответственно для диагональных и недиагональных элементов:
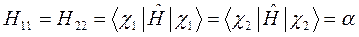
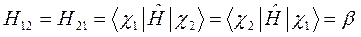
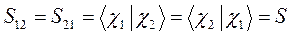
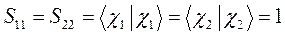
здесь матричные элементы определителя:
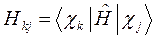
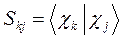
представляют собой интегралы, имеющие размерность энергии: 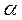 - кулоновский интеграл;
- кулоновский интеграл; 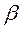 - обменный (резонансный) интеграл и
- обменный (резонансный) интеграл и 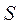 - интеграл перекрывания.
- интеграл перекрывания.
Итак, в ходе преобразований мы пришли к определителю вида:
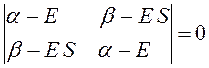
Раскрывая определитель и решая получившееся квадратное уравнение, получаем два значения для энергии, соответствующие симметричному и несимметричному решениям:
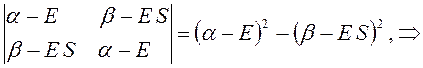
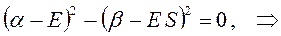
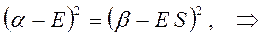
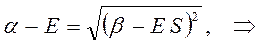
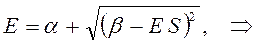
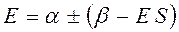
раскрывая скобки в полученном выражении, имеем:
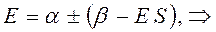
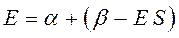
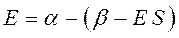
Рассмотрим уравнение вида:
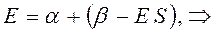
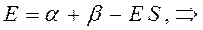
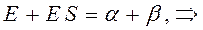
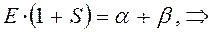
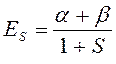
аналогично получаем:
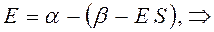
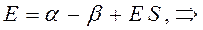
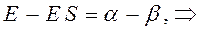
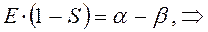
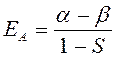
Составим уравнение для нахождения вариационных коэффициентов. Из полученной выше системы линейных уравнений:
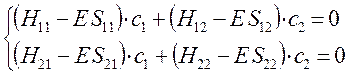
с учётом приведенных выше соображений следует, что:
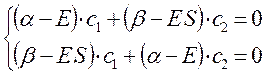
Коэффициенты 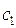 и
и 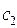 можно получить, если подставить найденные значения энергии в полученную в ходе преобразований систему. Однако необходимо заметить, что из двух однородных уравнений нельзя получить три неизвестных
можно получить, если подставить найденные значения энергии в полученную в ходе преобразований систему. Однако необходимо заметить, что из двух однородных уравнений нельзя получить три неизвестных 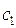 ,
, 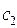 и
и 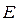 , а лишь одно из них и отношение двух других. Найдя
, а лишь одно из них и отношение двух других. Найдя 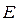 , мы можем теперь получить отношение величин
, мы можем теперь получить отношение величин 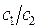 . Итак, в ходе преобразований, система линейных однородных уравнений:
. Итак, в ходе преобразований, система линейных однородных уравнений:
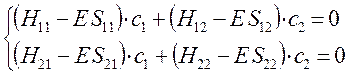
была преобразована нами к виду:
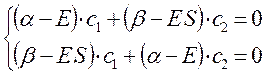
Из первого уравнения:
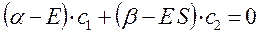
следует, что:
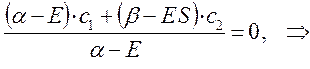
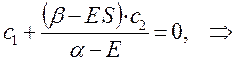
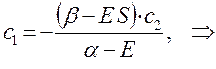
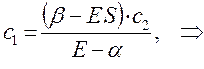
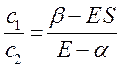
учитывая, что:
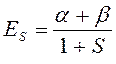
будем иметь соответственно:
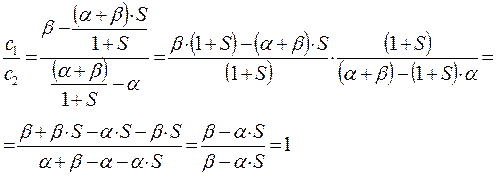
таким образом, имеем соотношение:
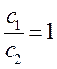
которое может быть преобразовано далее к виду:
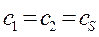
Аналогичные преобразования проведём и над вторым уравнением:
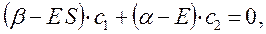
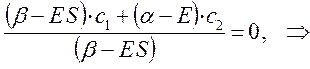
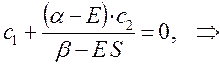
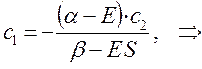
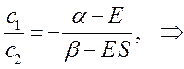
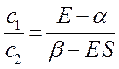
Учитывая, что:
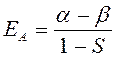
будем иметь соответственно:
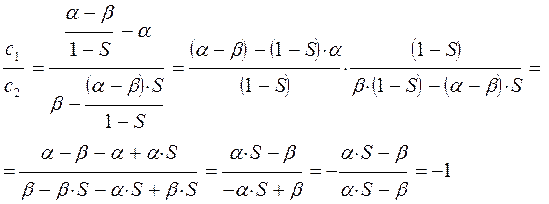
таким образом, имеем соотношение:
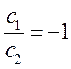
которое может быть преобразовано далее к виду:
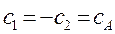
подстановка значений:
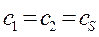
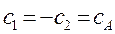
в разложение пробной волновой функции 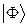 по базисному набору
по базисному набору 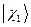 и
и 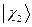 :
:
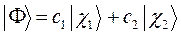
приводит к двум решениям – симметричному и ассиметричному, вида:
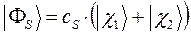
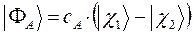
Для определения самих коэффициентов 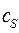 и
и 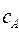 , воспользуемся условием нормировки:
, воспользуемся условием нормировки:
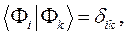
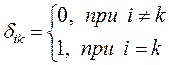
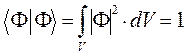
подставим сюда выражение для 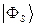 :
:
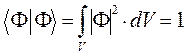
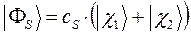
имеем таким образом:
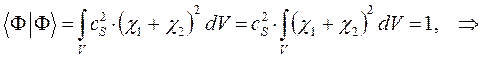
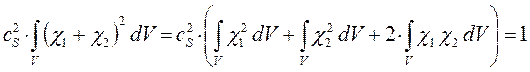
учитывая, что:
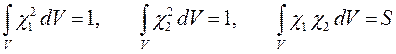
имеем:
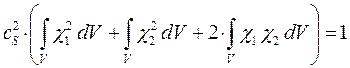
откуда соответственно:
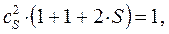
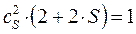
или в окончательном виде:
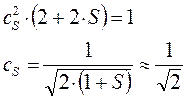
Аналогичным образом получим выражение и для коэффициента 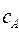 :
:
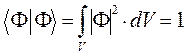
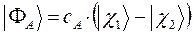
после соответствующих преобразований, получаем выражение вида:
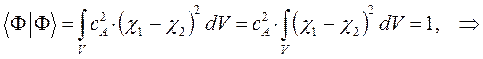
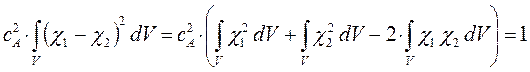
учитывая также, что:
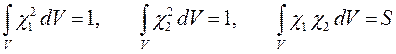
имеем:
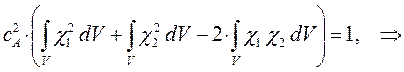
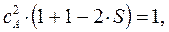
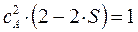
или в окончательном виде:
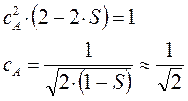
Таким образом, в ходе проделанных выкладок, приходим соответственно к выражениям для энергий и соответствующих им волновых функций симметричного и антисимметричного состояний квантово-механической системы:
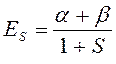
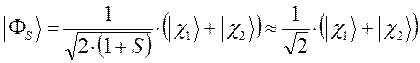
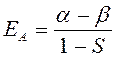
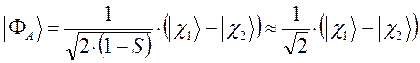
как это следует из решений уравнения Шрёдингера, эти орбитали ортогональны:
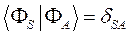
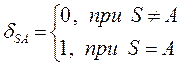
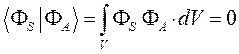
в этом легко убедиться:
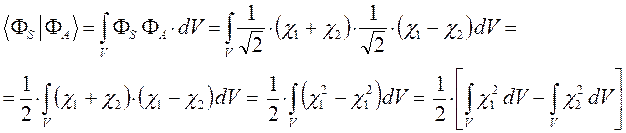
поскольку по определению:
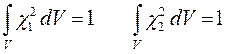
тогда соответственно:
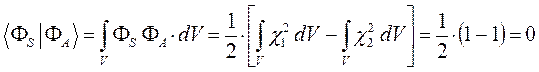
и таким образом:
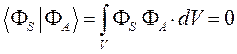
Рассмотрим теперь более подробней выражения для энергии:
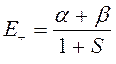
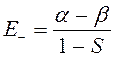
в них входят так называемые матричные элементы:
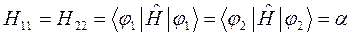
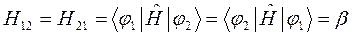
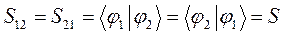
все эти элементы зависят от параметра 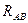 - межъядерного расстояния.
- межъядерного расстояния.
Кулоновский интеграл 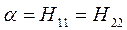 :
:
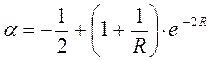
На языке квантовой механики передаёт классическое кулоновское взаимодействие частиц. Он включает в себя энергию электрона в атоме водорода в основном состоянии, кулоновское отталкивание ядер для случая молекул и энергию кулоновского взаимодействия одного из ядер многоэлектронной системы с электронным облаком окружающем другое ядро. На расстояниях порядка равновесного межъядерного и выше, этот интеграл отрицателен и на больших, где отталкивание ядер мало, равен энергии электрона атомной орбитали 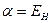 . Это означает, что кулоновский интеграл приближённо равен энергии электрона в атоме водорода и на основании теоремы Купманса, его можно оценить по значению энергии ионизации атомной орбитали. Только на очень малых расстояниях, по-сравнению с равновесным, он становится положительным и неограниченно возрастает.
. Это означает, что кулоновский интеграл приближённо равен энергии электрона в атоме водорода и на основании теоремы Купманса, его можно оценить по значению энергии ионизации атомной орбитали. Только на очень малых расстояниях, по-сравнению с равновесным, он становится положительным и неограниченно возрастает.
Обменный (резонансный) интеграл 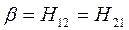 :
:
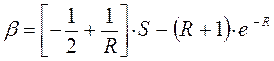
Энергия, выражаемая интегралом 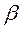 , не имеет аналога в классической механике.
, не имеет аналога в классической механике.
В резонансном (обменном) интеграле:
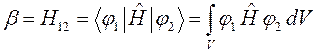
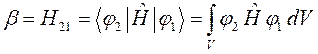
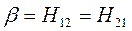
координаты электрона для функций 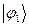 и
и 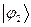 - разные,
- разные, 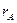 и
и 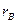 - тоже различны. В общем случае интеграл
- тоже различны. В общем случае интеграл 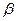 описывает то добавочное понижение энергии, которое возникает из-за возможности перехода электрона от ядра атома
описывает то добавочное понижение энергии, которое возникает из-за возможности перехода электрона от ядра атома 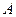 к ядру атома
к ядру атома 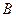 , возможности движения электрона в поле двух ядер, как бы «обменивая» ядра при этом, обменивая состояние
, возможности движения электрона в поле двух ядер, как бы «обменивая» ядра при этом, обменивая состояние 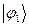 на состояние
на состояние 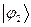 . Возникновение такого рода обменного взаимодействия, возникновение обменных сил формально связано с эрмитовостью оператора Гамильтона
. Возникновение такого рода обменного взаимодействия, возникновение обменных сил формально связано с эрмитовостью оператора Гамильтона 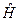 . Этот интеграл на бесконечности равен нулю, на всех других, кроме ультракоротких – отрицателен. Только на очень коротких расстояниях, достаточных для возникновения химической связи он становится положительным и возрастает неограниченно. Именно на таких расстояниях становится возможным возникновение обменных сил и как следствие – образование химической связи. Именно его вклад и определяет энергию химической связи: чем он больше, тем прочнее будет химическая связь.
. Этот интеграл на бесконечности равен нулю, на всех других, кроме ультракоротких – отрицателен. Только на очень коротких расстояниях, достаточных для возникновения химической связи он становится положительным и возрастает неограниченно. Именно на таких расстояниях становится возможным возникновение обменных сил и как следствие – образование химической связи. Именно его вклад и определяет энергию химической связи: чем он больше, тем прочнее будет химическая связь.
Интеграл перекрывания 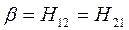 :
:
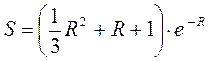
Этот интеграл служит мерой перекрывания атомных орбиталей, образующих молекулярную орбиталь. Интеграл перекрывания – безразмерная величина. Он равен единице, при 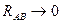 и спадает до нуля, при возрастании межъядерного расстояния
и спадает до нуля, при возрастании межъядерного расстояния 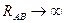 . При увеличении
. При увеличении 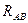 , величина интеграла перекрывания убывает экспоненциально. В общем случае, на расстояниях между атомами, существующими в молекулах, обменный интеграл тем больше по абсолютной величине, чем больше интеграл перекрывания, т.е. между обменным интегралом и интегралом перекрывания существует линейная зависимость
, величина интеграла перекрывания убывает экспоненциально. В общем случае, на расстояниях между атомами, существующими в молекулах, обменный интеграл тем больше по абсолютной величине, чем больше интеграл перекрывания, т.е. между обменным интегралом и интегралом перекрывания существует линейная зависимость 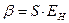 . Поэтому принято считать, что чем больше перекрываются атомные орбитали соответствующих атомов, партнёров по связи, образующие молекулярные орбитали, тем прочнее связь. Это утверждение лежит в основе принципа максимального перекрывания. Требование, чтобы перекрывание атомных орбиталей при образовании молекулярных орбиталей, есть, таким образом, требованием, чтобы расположение атомных ядер в молекуле отвечало максимальной её устойчивости. Установив вид зависимости интегралов
. Поэтому принято считать, что чем больше перекрываются атомные орбитали соответствующих атомов, партнёров по связи, образующие молекулярные орбитали, тем прочнее связь. Это утверждение лежит в основе принципа максимального перекрывания. Требование, чтобы перекрывание атомных орбиталей при образовании молекулярных орбиталей, есть, таким образом, требованием, чтобы расположение атомных ядер в молекуле отвечало максимальной её устойчивости. Установив вид зависимости интегралов 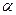 ,
, 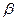 и
и 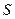 от межъядерного расстояния, можно найти взаимное расположение уровней энергии
от межъядерного расстояния, можно найти взаимное расположение уровней энергии 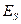 и
и 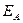 . На всех расстояниях, кроме очень коротких,
. На всех расстояниях, кроме очень коротких, 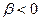 ; вследствие этого
; вследствие этого 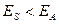 . Поэтому
. Поэтому 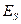 отвечает основному состоянию, а
отвечает основному состоянию, а 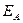 - первому возбуждённому состоянию в молекуле (например, в молекуле
- первому возбуждённому состоянию в молекуле (например, в молекуле 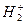 ). В связи с тем, что
). В связи с тем, что 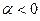 и
и 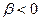 , уровень энергии молекулярной орбитали
, уровень энергии молекулярной орбитали 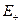 , определяемой выражением:
, определяемой выражением:
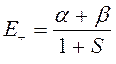
будет находиться на диаграмме ниже, уровня энергии молекулярной орбитали 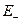 :
:
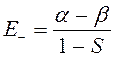
После того как получены орбитальные энергии, их представляют на энергетической диаграмме. Диаграмма состоит из трёх частей. Слева и справа показывают энергетические уровни отдельных атомов водорода, а в центральной части – энергетические уровни (молекулярные орбитали) молекулярного иона водорода. В соответствии с правилами, аналогичными правилам заполнения атомных орбиталей (принципом наименьшей энергии, принципом Паули и правилом Гунда), единственный электрон в ионе 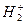 будет заселять нижний по энергии уровень
будет заселять нижний по энергии уровень 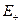 . Отметим, что этот уровень расположен ниже, чем соответствующие уровни отдельных атомов водорода
. Отметим, что этот уровень расположен ниже, чем соответствующие уровни отдельных атомов водорода 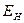 . Таким образом, состояние
. Таким образом, состояние 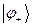 , является энергетически выгодным. В связи с этим молекулярную орбиталь
, является энергетически выгодным. В связи с этим молекулярную орбиталь 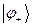 называют связывающей молекулярной орбиталью. Нахождение электрона на этой орбитали приводит к понижению полной энергии системы по сравнению с энергией составных частей. Второе состояние, описываемое волновой функцией
называют связывающей молекулярной орбиталью. Нахождение электрона на этой орбитали приводит к понижению полной энергии системы по сравнению с энергией составных частей. Второе состояние, описываемое волновой функцией 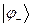 , называют разрыхляющей (или антисвязывающей) молекулярной орбитали. Как это очевидно из приведенной выше энергетической диаграммы, энергия данного состояния выше энергий соответствующих исходных атомных орбиталей. Нахождение электрона на данной молекулярной орбитали приводит к повышению полной энергии системы и как следствие, приводит к уменьшению энергии связывания атомов партнёров по связи. Таким образом, расчёт вариационным методом даёт два состояния для одного электрона в молекулярном ионе водорода: связывающее
, называют разрыхляющей (или антисвязывающей) молекулярной орбитали. Как это очевидно из приведенной выше энергетической диаграммы, энергия данного состояния выше энергий соответствующих исходных атомных орбиталей. Нахождение электрона на данной молекулярной орбитали приводит к повышению полной энергии системы и как следствие, приводит к уменьшению энергии связывания атомов партнёров по связи. Таким образом, расчёт вариационным методом даёт два состояния для одного электрона в молекулярном ионе водорода: связывающее 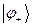 и разрыхляющее
и разрыхляющее 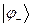 состояния. Связывающее состояние
состояния. Связывающее состояние 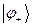 , соответствует более низкому по сравнению с отдельными атомами значению энергии. Связывание характеризуется повышенной вероятностью нахождения электрона в пространстве между ядрами. Разрыхляющее состояние
, соответствует более низкому по сравнению с отдельными атомами значению энергии. Связывание характеризуется повышенной вероятностью нахождения электрона в пространстве между ядрами. Разрыхляющее состояние 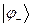 , соответствует более высокому по сравнению с отдельными атомами значению энергии. Разрыхление характеризуется пониженной вероятностью нахождения электрона в пространстве между ядрами. Зависимость энергии молекулярного иона водорода от межъядерного расстояния, удобнее всего представлять в виде так называемой энергетической кривой, описывающей диссоциацию двухатомных молекул на атомы. Как это хорошо видно, она имеет минимум на расстоянии
, соответствует более высокому по сравнению с отдельными атомами значению энергии. Разрыхление характеризуется пониженной вероятностью нахождения электрона в пространстве между ядрами. Зависимость энергии молекулярного иона водорода от межъядерного расстояния, удобнее всего представлять в виде так называемой энергетической кривой, описывающей диссоциацию двухатомных молекул на атомы. Как это хорошо видно, она имеет минимум на расстоянии 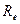 , которое называют равновесным расстоянием; а глубина этого минимума определяет энергию диссоциации
, которое называют равновесным расстоянием; а глубина этого минимума определяет энергию диссоциации 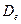 . Смысл понятий связывание и антисвязывание (разрыхление), находит своё наглядное отображение, при рассмотрении задачи о движении частицы в центральном поле сил. Как известно, в центральном поле сил, потенциальная энергия частицы (системы частиц) зависит от расстояния между частицей (системой частиц) и центром силового поля. Обычно для наглядности, задачу о движении в центральном поле сил сводят к двум моделям – модели гармонического осциллятора и движении частицы в кулоновском поле сил. Как известно, гармонический осциллятор представляет собой колебательную систему, которая совершает свободные (собственные) незатухающие механические колебания, совершаемые без внешнего воздействия за счёт первоначально полученной телом энергии. При рассмотрении колебаний такого вида – пренебрегают силой сопротивления, а совершающиеся непрерывные осциллирующие движения рассматривают как гармонические, т.е. как такие, что совершаются в системе по закону синуса или косинуса. Такие непрерывные колебательные движения, очевидно, могут осуществляться только под действием квазиупругой силы, т.е. такой, что возникает в системе при малых деформациях. Поскольку, в случае гармонического осциллятора, колебательное движение будет совершаться под действием упругой возвращающей силы, то при малых деформациях частица (система частиц) в данном случае, будет совершать колебания относительно положения равновесия. Поскольку квазиупругая сила является консервативной по своей природе, поэтому полная энергия такой системы должна оставаться постоянной. При этом, как было показано уже в предыдущих разделах, полная энергия гармонического осциллятора может быть задана выражение:
. Смысл понятий связывание и антисвязывание (разрыхление), находит своё наглядное отображение, при рассмотрении задачи о движении частицы в центральном поле сил. Как известно, в центральном поле сил, потенциальная энергия частицы (системы частиц) зависит от расстояния между частицей (системой частиц) и центром силового поля. Обычно для наглядности, задачу о движении в центральном поле сил сводят к двум моделям – модели гармонического осциллятора и движении частицы в кулоновском поле сил. Как известно, гармонический осциллятор представляет собой колебательную систему, которая совершает свободные (собственные) незатухающие механические колебания, совершаемые без внешнего воздействия за счёт первоначально полученной телом энергии. При рассмотрении колебаний такого вида – пренебрегают силой сопротивления, а совершающиеся непрерывные осциллирующие движения рассматривают как гармонические, т.е. как такие, что совершаются в системе по закону синуса или косинуса. Такие непрерывные колебательные движения, очевидно, могут осуществляться только под действием квазиупругой силы, т.е. такой, что возникает в системе при малых деформациях. Поскольку, в случае гармонического осциллятора, колебательное движение будет совершаться под действием упругой возвращающей силы, то при малых деформациях частица (система частиц) в данном случае, будет совершать колебания относительно положения равновесия. Поскольку квазиупругая сила является консервативной по своей природе, поэтому полная энергия такой системы должна оставаться постоянной. При этом, как было показано уже в предыдущих разделах, полная энергия гармонического осциллятора может быть задана выражение:
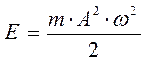
Действительно, в процессе колебательного движения, происходит превращение кинетической энергии в потенциальную и обратно, причём в моменты наибольшего отклонения от положения равновесия, полная энергия системы будет состоять, только из потенциальной энергии, которая при этом будет достигать своего наибольшего значения 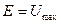 . Точки, в которых потенциальная энергия равна полной энергии
. Точки, в которых потенциальная энергия равна полной энергии 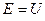 , называют точками остановки. В точках остановки (поворота) кинетическая энергия обращается в нуль. Если движение материальной точки происходит между двумя точками остановки, его называют финитным. Если же движение не ограничено или ограничено только одной точкой остановки, то его называют инфинитным. В соответствии с выше изложенным, можно заключить, что гармонический осциллятор совершает одномерное финитное движение. Это означает, что частица совершает периодически повторяющиеся движения между двумя точками остановки. Такое движение называют колебательным. При финитном движении в точках остановки кинетическая энергия осциллятора обращается в нуль и полная его энергия равна его потенциальной энергии. В промежутках между двумя точками остановки, потенциальная энергия уменьшается и при прохождении через положение равновесия – обращается в нуль. В этом случае полная энергия системы будет равна его кинетической энергии. При рассмотрении движения частицы с зарядом
, называют точками остановки. В точках остановки (поворота) кинетическая энергия обращается в нуль. Если движение материальной точки происходит между двумя точками остановки, его называют финитным. Если же движение не ограничено или ограничено только одной точкой остановки, то его называют инфинитным. В соответствии с выше изложенным, можно заключить, что гармонический осциллятор совершает одномерное финитное движение. Это означает, что частица совершает периодически повторяющиеся движения между двумя точками остановки. Такое движение называют колебательным. При финитном движении в точках остановки кинетическая энергия осциллятора обращается в нуль и полная его энергия равна его потенциальной энергии. В промежутках между двумя точками остановки, потенциальная энергия уменьшается и при прохождении через положение равновесия – обращается в нуль. В этом случае полная энергия системы будет равна его кинетической энергии. При рассмотрении движения частицы с зарядом 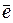 в кулоновском поле постоянного потенциала, создаваемого
в кулоновском поле постоянного потенциала, создаваемого
другой частицей с зарядом 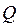 , нами были получены неравенства вида:
, нами были получены неравенства вида:
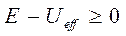
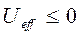
Отсюда хорошо видно, что при 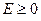 область движения становится не ограниченной и движение становится инфинитным. В этом случае эффективная сила
область движения становится не ограниченной и движение становится инфинитным. В этом случае эффективная сила 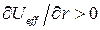 - направлена от центра, и частица уходит в бесконечность. Иными словами, инфинитному движению соответствует несвязанное состояние. При
- направлена от центра, и частица уходит в бесконечность. Иными словами, инфинитному движению соответствует несвязанное состояние. При 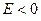 , движение совершается в ограниченной области пространства – финитное движение. В данном случае частица находится вблизи силового центра, а эффективная сила направлена к силовому центру, связанному с частицей
, движение совершается в ограниченной области пространства – финитное движение. В данном случае частица находится вблизи силового центра, а эффективная сила направлена к силовому центру, связанному с частицей 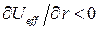 . Теоретическим обобщением введенных представлений о связывающем и антисвязывающем состояниях, являются теоремы вириала и Гельмана-Фейнмана. Последние являются критериями точности получаемых в ходе решения волнового уравнения волновых функций, вследствие приближённого характера квантово-механических расчётов. Необходимость учёта этих критериев определяется приемлемостью или неприемлемостью получаемых в ходе расчётов волновых функций. Приемлемость в свою очередь зависит от характера решаемой задачи; волновая функция, удовлетворяющая одной задаче, становится неприемлемой в условиях другой задачи. Так, для молекул, рассматриваемых в адиабатическом приближении с одной стороны – предполагается наличие некоторых внешних сил действующих на ядра и фиксирующих последние. С другой стороны – на каждое ядро действует сила притяжения со стороны сферически симметричных зарядов, центрированных на ядрах и заряда перекрывания, центрированного посредине между ядрами. «Собственный» сферический заряд, разумеется, не оказывает на ядро никакого влияния. В свою очередь другой сферический заряд будет также незначительно экранировать «своё» ядро, что приведёт к незначительному взаимному отталкиванию ядер. При этом данное «отталкивательное состояние» увеличится при условии концентрации электронной плотности за ядрами атомов; в данном случае электроны, концентрируясь за ядрами атомов образующих молекулу (случай инфинитного движения), будут притягивать последние к себе, увеличивая тем самым отталкивание между ядрами. И напротив, концентрация электронной плотности между ядрами (случай финитного движения), приведёт к «стягиванию» последних. Таким образом, уже на данном этапе можно увидеть постановку вопроса о наличии в молекуле двух противоположных представлений о связующем и отталкивательном (антисвязующем или разрыхляющем) состояниях. Впервые данные понятия были введены в науку и стали понятными с развитием метода молекулярных орбиталей, чем и определяется перспективность последнего в сравнении с другим квантовохимическим подходом – методом валентных связей, который по-существу является переведенной на квантово-механический язык теорией Льюиса. Следует сразу сказать, что обе эти интерпретации, в сущности, эквивалентны и различаются только терминологией, поскольку теорема вириала и Гельмана-Фейнмана имеют единую квантово-механическую основу. С одной стороны – некоторые внешние силы фиксируют положение ядер в пространстве, с другой стороны – это становится возможным только благодаря локализации электронов относительно ядер, т.е. определяется распределением электронной плотности. Первое утверждение составляет суть теоремы вириала, второе утверждение – теоремы Гельмана-Фейнмана. Эти две теоремы взаимосвязаны, однако необходимо заметить, что содержание теоремы Гельмана-Фейнмана – следствие более общей по-своему содержанию теоремы вириала, согласно которой средняя кинетическая энергия электрона возрастает при образовании молекулы:
. Теоретическим обобщением введенных представлений о связывающем и антисвязывающем состояниях, являются теоремы вириала и Гельмана-Фейнмана. Последние являются критериями точности получаемых в ходе решения волнового уравнения волновых функций, вследствие приближённого характера квантово-механических расчётов. Необходимость учёта этих критериев определяется приемлемостью или неприемлемостью получаемых в ходе расчётов волновых функций. Приемлемость в свою очередь зависит от характера решаемой задачи; волновая функция, удовлетворяющая одной задаче, становится неприемлемой в условиях другой задачи. Так, для молекул, рассматриваемых в адиабатическом приближении с одной стороны – предполагается наличие некоторых внешних сил действующих на ядра и фиксирующих последние. С другой стороны – на каждое ядро действует сила притяжения со стороны сферически симметричных зарядов, центрированных на ядрах и заряда перекрывания, центрированного посредине между ядрами. «Собственный» сферический заряд, разумеется, не оказывает на ядро никакого влияния. В свою очередь другой сферический заряд будет также незначительно экранировать «своё» ядро, что приведёт к незначительному взаимному отталкиванию ядер. При этом данное «отталкивательное состояние» увеличится при условии концентрации электронной плотности за ядрами атомов; в данном случае электроны, концентрируясь за ядрами атомов образующих молекулу (случай инфинитного движения), будут притягивать последние к себе, увеличивая тем самым отталкивание между ядрами. И напротив, концентрация электронной плотности между ядрами (случай финитного движения), приведёт к «стягиванию» последних. Таким образом, уже на данном этапе можно увидеть постановку вопроса о наличии в молекуле двух противоположных представлений о связующем и отталкивательном (антисвязующем или разрыхляющем) состояниях. Впервые данные понятия были введены в науку и стали понятными с развитием метода молекулярных орбиталей, чем и определяется перспективность последнего в сравнении с другим квантовохимическим подходом – методом валентных связей, который по-существу является переведенной на квантово-механический язык теорией Льюиса. Следует сразу сказать, что обе эти интерпретации, в сущности, эквивалентны и различаются только терминологией, поскольку теорема вириала и Гельмана-Фейнмана имеют единую квантово-механическую основу. С одной стороны – некоторые внешние силы фиксируют положение ядер в пространстве, с другой стороны – это становится возможным только благодаря локализации электронов относительно ядер, т.е. определяется распределением электронной плотности. Первое утверждение составляет суть теоремы вириала, второе утверждение – теоремы Гельмана-Фейнмана. Эти две теоремы взаимосвязаны, однако необходимо заметить, что содержание теоремы Гельмана-Фейнмана – следствие более общей по-своему содержанию теоремы вириала, согласно которой средняя кинетическая энергия электрона возрастает при образовании молекулы:
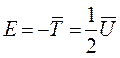
В наглядном классическом представлении, электрон должен двигаться в поле двух ядер быстрее, чем в атоме. Но средняя потенциальная энергия 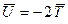 сильно понижается в результате притяжения к двум ядрам. Общее понижение энергии
сильно понижается в результате притяжения к двум ядрам. Общее понижение энергии 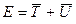 есть, таким образом, результат преобладающего понижения потенциальной энергии электрона. Поэтому система из двух ядер и электрона оказывается более устойчивой, чем система разъединённых ядер, иными словами, благодаря понижению потенциальной энергии электрона возникает химическая связь. Характерной её особенностью является обобществление электрона всеми ядрами молекулы. До сих пор нами рассматривался случай, когда две области А и В – физически эквивалентные области (симметрия) и средняя энергия электрона в такой системе одинакова. Рассмотрим теперь кратко, в самых общих чертах случай, когда области А и В в рассматриваемой системе физически различны, т.е. равенство:
есть, таким образом, результат преобладающего понижения потенциальной энергии электрона. Поэтому система из двух ядер и электрона оказывается более устойчивой, чем система разъединённых ядер, иными словами, благодаря понижению потенциальной энергии электрона возникает химическая связь. Характерной её особенностью является обобществление электрона всеми ядрами молекулы. До сих пор нами рассматривался случай, когда две области А и В – физически эквивалентные области (симметрия) и средняя энергия электрона в такой системе одинакова. Рассмотрим теперь кратко, в самых общих чертах случай, когда области А и В в рассматриваемой системе физически различны, т.е. равенство:
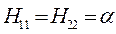
не выполняется, но перекрыванием области можно пренебречь:
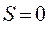
Это возвращает нас к обычной вековой задаче:
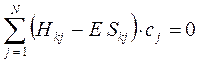
или в матричном виде, применительно к рассматриваемой задаче:
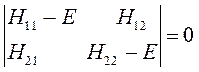
или
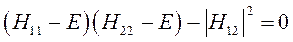
Решение соответствующего квадратного уравнения:
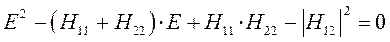
приводит к решению вида:
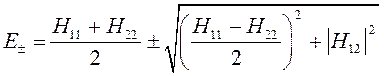
Решение такого типа характерно для молекул с несимметричным распределением электронной плотности – случай гетероядерных молекул.
 2015-04-08
2015-04-08 2550
2550






