2015-04-08
2579
Особое место в решении прогнозных задач отводится моделям с лаговыми переменными. Это вполне естественно, так как воздействие многих экономических факторов на результирующий показатель проявляется не мгновенно, а с некоторым запаздыванием. При выработке экономической стратегии модели подобного типа позволяют получить ответ на вопрос: «Что необходимо делать сегодня, чтобы получить желаемый результат в будущем?» Можно указать ряд причин, порождающих механизмы запаздывания во взаимодействии экономических факторов:
1) Институциональные причины. Прежде всего, к этим причинам относятся контрактные отношения между различными хозяйствующими субъектами, предполагающие поддержание некоторой стабильности на протяжении определенного отрезка времени. Стабильность в отношениях создает стабильность экономического взаимодействия, порождающего, в свою очередь, лаговый механизм получения результатов.
2) Психологические причины. Проявление этих причин осуществляется через инерционное поведение людей. Так, люди тратят свои доходы не сразу, а постепенно. Они следуют определенному, привычному для них, образу жизни, в частности, стремятся к поддержанию достигнутого уровня жизни, приобретая привычные блага даже в момент падения своих доходов. Следовательно, в самом поведении человека, в принимаемых им решениях проявляется своеобразный лаговый механизм.
|
|
|
3) Технологические причины. Эти причины непосредственно связаны с инерционностью проявления научно-технического прогресса. Очевидно, что эффект от замены старого оборудования новым проявляется не мгновенно, а через некоторое время.
4) Механизм взаимодействия экономических показателей. Многие экономические явления, обладая инерционностью, продолжают оказывать свое воздействие на соответствующие показатели в течение длительного периода времени. Например, инфляция, проявившись однажды, воздействует на такие макроэкономические показатели, как уровень спроса, безработицы, сбережений, достаточно длительное время. Известный мультипликатор Кейнса оказывает положительное влияние на экономику в течение определенного временного интервала.
Формальным представлением запаздываний во взаимодействии экономических показателей являются модели с различной структурой лагов. В качестве примеров рассмотрим модель с конечным числом лагов
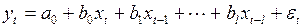(3.130)
и модель с бесконечным числом лагов
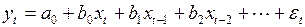, (3.131)
где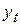 
– значение моделируемого показателя в момент времени 
;
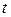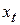– значение фактора в момент времени ;
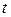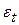– случайная величина;
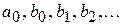– параметры моделей
Методы построения этих моделей различны, поскольку зависят от числа лагов – конечного или бесконечного. И в той, и другой модели коэффициент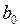 
принято называть краткосрочным мультипликатором, так как с его помощью оценивается изменение среднего значения 
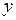под воздействием единичного изменения переменной 
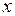в тот же самый момент времени. Сумма всех коэффициентов 
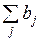называют долгосрочным мультипликатором. С его помощью характеризуют изменение 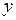под воздействием единичных изменений переменной 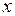в каждом из учитываемых моделью временных периодов. Любая частичная сумма 
(
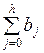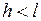) называется промежуточным мультипликатором.
|
|
|
Для оценивания коэффициентов с конечным числом лагов можно использовать обычный МНК, так как, по сути, она представляет собой уравнение множественной регрессии. Правда, при построении этих моделей часто приходится сталкиваться с проблемами мультиколлинеарности. Для оценки коэффициентов модели с бесконечным числом лагов разработаны специальные методы, к рассмотрению которых мы переходим.
Метод Койка основан на естественном предположении о том, что степень влияния лаговой переменной убывает по мере возрастания лага. Причем, такое убывание происходит согласно закону, описываемому геометрической прогрессией, т.е. коэффициенты при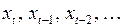 
соответственно равны 
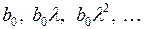. Таким образом, в общем случае 
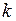-й коэффициент модели с бесконечным числом лагов можно записать в виде
, 
, 
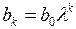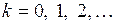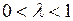. (3.132)
Используя такое представление коэффициентов, модель с бесконечным числом лагов можно преобразовать в следующее уравнение:
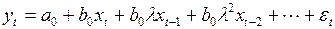. (3.133)
В результате проведенного преобразования получена модель всего с тремя неизвестными коэффициентами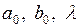 
, которые можно определить различными способами. Один из методов предусматривает подбор параметра 
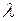из интервала 
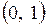. Для этого параметру 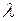последовательно присваиваются значения с некоторым фиксированным шагом 
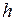(например, 
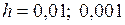) и для каждого так полученного значения 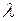рассчитывается
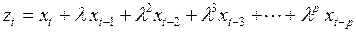, (3.134)
где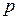 
– количество лагов, участвующих в расчете.
Величина 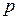определяется из условия, что дальнейшее добавление лаговых значений практически не изменяет величину 
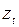, т.е. изменение 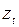, вызванное добавлением 
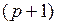-го лага, меньше ранее заданного положительного числа. Замена лаговых переменных одной интегрированной сводит задачу построения модели с лаговыми переменными к оцениванию коэффициентов уравнения
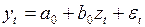(3.135)
и выбору того значения 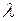, при котором коэффициент детерминации уравнения (3.135) будет наибольшим. Полученные таким образом параметры 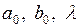подставляются в уравнение (3.133), которое готово для проведения прогнозных расчетов.
Второй метод построения модели с бесконечным числом лагом основан на преобразовании Койка. Для выполнения этого преобразования запишем уравнение для момента времени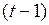 
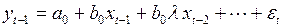. (3.136)
Умножим полученное уравнение на 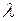и вычтем его из (3.133). Получим следующее уравнение:
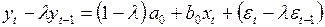, (3.137)
которое можно переписать в виде
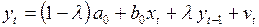, (3.138)
где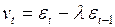 
– скользящая средняя.
Полученное уравнение является результатом преобразования Койка. Оно не содержит бесконечного числа лагов с убывающими по закону геометрической прогрессии коэффициентами и представляет собой уравнение с авторегрессионным членом (3.138). Для его построения необходимо оценить всего три коэффициента 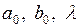. Модель (3.138), несмотря на компактность своей записи, позволяет анализировать краткосрочные и долгосрочные эффекты переменных. В краткосрочном периоде значение 
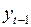можно считать фиксированным. Тогда краткосрочный мультипликатор равен .
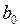Долгосрочный мультипликатор вычисляется по формуле суммы бесконечно убывающей геометрической прогрессии. Если далее предположить, что в долгосрочном периоде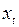 
стремится к некоторому своему равновесному значению 
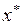, то значение 
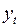также стремится к своему равновесному значению 
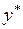. Для равновесного состояния уравнение (3.138) без учета случайного отклонения примет вид
|
|
|
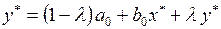(3.139)
и можно определить равновесное значение
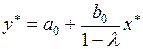. (3.140)
Коэффициент, стоящий при 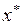в (3.140), является долгосрочном мультипликатором, так как он в соответствии с известной формулой является суммой бесконечно убывающей геометрической прогрессии, т.е.
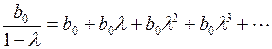. (3.141)
Очевидно, что при 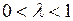сила воздействия долгосрочного мультипликатора превосходит силу воздействия краткосрочного, поскольку 
.
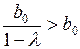Применение МНК для оценки параметров лаговой модели, полученной с помощью преобразования Койка, не всегда корректно в силу следующих обстоятельств:
1) Переменная 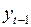, которая используется как независимая переменная, имеет стохастическую природу, как и 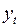, что нарушает одну из предпосылок МНК. Кроме того, она скорее коррелирует со случайной составляющей 
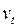, чем не коррелирует.
2) Несмотря на то, что для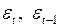 
предпосылки МНК выполняются, но для 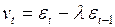имеет место явная автокорреляция, которую можно тестировать 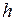-статистикой Дарбина.
Если не применять специальных методов оценивания, то, возможно, что полученные оценки коэффициентов этой модели окажутся смещенными и несостоятельными.
Распределенные лаги Алмон. На коэффициенты уравнения регрессии, при построении которого используется преобразование Койка, накладываются достаточно жесткие ограничения, которые связаны с предположением о том, что значения коэффициентов при лаговых переменных убывают в геометрической последовательности. Целесообразность этих предположений, как показывает практика, не во всех случаях себя оправдывает. Весьма реальна ситуация, когда, например, значения лаговой переменной с запаздыванием на 2 и 3 периода оказывают на зависимую переменную более сильное влияние, чем текущее и предшествующее текущему значение, т.е.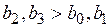 
. Для моделирования подобных ситуаций достаточно гибким инструментом является аппарат распределенных лагов Алмон.
Модель Алмон строится в предположении, что значения коэффициентов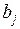 
могут быть аппроксимированы полиномами соответствующей степени от величины лага 
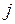, т.е.
|
|
|
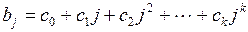. (3.142)
Реализация этого предположения позволяет каждый из коэффициентов лаговой модели представить в виде:
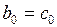
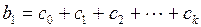
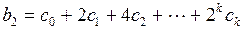
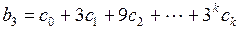(3.143)
.
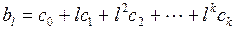Подставить в уравнение (3.142) вместо коэффициентов полиномы, их аппроксимирующие, получим выражение
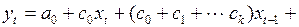
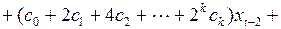
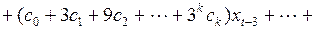(3.144)
.
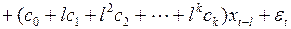После перегруппировки слагаемых это выражение переписывается в виде
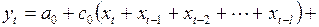
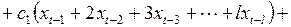
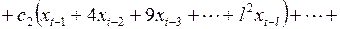(3.145)
.
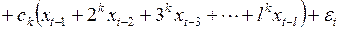Если ввести новые переменные
, 
, 
,..., 
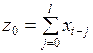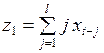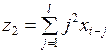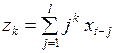, (3.146)
и заменить ими в (3.145) выражения в круглых скобках, то модель с распределенными лагами может быть представлена в виде регрессионной модели
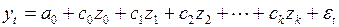, (3.147)
коэффициенты которой можно оценить с помощью МНК.
Все проведенные рассуждения и преобразования имеют смысл, если известна величина максимального лага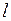 
и определен порядок полинома, описывающего структура лага. В практических ситуациях, как правило, такая информация отсутствует. Поэтому величину лага 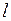и порядок полинома 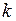определяют в процессе построения модели.
Последовательность процедур, выполняемых при использовании метода Алмон для построения моделей с распределенными лагами, следующая:
1) определяется максимальный лаг ;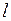
2) определяется степень полинома ;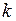
3) рассчитываются с помощью (3.146) значения переменных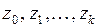 
;
4) оцениваются с помощью МНК параметры уравнения линейной регрессии (3.147);
5) рассчитываются параметры исходной модели с помощью соотношений (3.143).
Практическая реализация этих процедур требует определенных усилий. Проблема в том, что для некоторых из выше приведенных пунктов нет единых рекомендаций их выполнения. Это касается 1), 2) и 4) пунктов. Логика построения этих моделей требует, чтобы величина максимального лага и степень полинома были определены до непосредственного построения модели, но процедуры их определения нельзя отнести к тривиальным.
Известно, что ошибки при определении этих величин приводят к построению неадекватных моделей. Причем, если установленный лаг 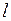оказался меньше реального, то это приводит к неверной спецификации модели, так как эта ситуация эквивалентна тому, что в регрессионной модели (4.147) учтены не все факторы и, следовательно, остатки будут коррелировать с зависимой переменной. А это значит, что не соблюдается предпосылка МНК о случайности остатков. Невыполнение этого условия приводит к получению смещенных и неэффективных оценок регрессионных коэффициентов.
В тех же случаях, когда 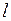превосходит реальную величину возникает ситуация аналогичная включению в модель статистически незначимого фактора. Нежелательный эффект от такой ошибки выражается в снижении эффективности получаемых с помощью МНК оценок. Но все же в этом случае оценки несмещенные и, поэтому ошибка с завышением величины лага приводит к меньшим искажениям модели, чем ошибка с заниженной его величиной.
Есть несколько подходов, которые решение этой проблемы переводят в практическую плоскость. Первый связан с построением нескольких альтернативных уравнений регрессии, в которых используется различные величины лагов, и выборе наилучшего из построенных уравнений. Очень важно, чтобы среди альтернативных вариантов оказались те уравнения, которые построены для максимально возможных лагов. Только в этом случае можно надеяться на получение истинной величины лага.
Второй подход основан на простом способе, предусматривающем измерение тесноты связи между зависимой переменной и всевозможными лаговыми значениями независимой переменной. В соответствии с этим подходом величина лага определяется по статистически значимой связи с переменной, имеющей максимальный лаг.
Вопрос о порядке полинома решается, в основном, путем сравнения моделей построенных с использованием полиномов различной степени. В практических расчетах обычно ограничиваются построением моделей, структура лага которых задается полиномом степени не выше трех. Выбирается та модель, которая тестируется как наиболее адекватная.
Последняя проблема, возникающая при построении модели (4.147), связана с обычно имеющей место мультиколлинеарностью переменных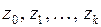 
, проявление которой сказывается на надежности получаемых оценок для 
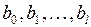. Однако их искажение значительно меньше, чем, если бы эти оценки были получены обычным МНК для регрессии на исходные лаговые переменные 
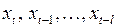. Для снижения эффекта мультиколлинеарности можно применять рекомендуемые для этих целей процедуры, но не все. Например, исключение некоторой части сильно коррелирующих между собой факторов здесь не применимо.
