Детерминированного факторного анализа

Детерминированный факторный анализ представляет собой методику исследования влияния факторов, связь которых с результативным показателем носит функциональный характер, т. е. результативный показатель может быть представлен в виде произведения, частного от деления или алгебраической суммы показателей, являющихся факторами детерминированной модели.

Основные свойства детерминированного подхода к анализу:

- определение детерминированной модели путем логического анализа;

- наличие полной (жесткой) связи между показателями;

- невозможность разделить результаты влияния одновременно действующих факторов, которые не поддаются объединению в одной модели;

- изучение взаимосвязей в краткосрочном периоде.

Этапы детерминированного факторного анализа:

1) построение экономически обоснованной детерминированной факторной модели;

2) выбор приема анализа и подготовка условий для его выполнения;

3) реализация счетных процедур;

4) формулирование выводов.

Таким образом, первоочередная задача факторного анализа состоит в построении модели, которая определяется путем логического анализа.

Типы детерминированных моделей:аддитивные; мультипликативные; кратные; смешанные.

Аддитивные модели представляют собой алгебраическую сумму показателей и имеют следующую математическую интерпретацию:

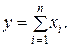(8)

В качестве примера можно привести балансовую модель товарного обеспечения:

N _{зап 0} + N _п = N _p + N _выб + N _{зап 1}, (9)

где N _{зап 0}–запасы товаров на начало периода; N _п –объем поступления; N _p –общий объем реализации; N _выб –прочее выбытие товаров; N _{зап 1}–запасы товаров на конец анализируемого периода.

Мультипликативная модель представляет собой произведение факторов. В обобщенном виде она может быть представлена формулой

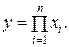(10)

Примером мультипликативной модели является двухфактор­ная модель объема реализации:

V _p = Ч · В, (11)

где Ч – среднесписочная численность работников; В – выработка на 1 работника.

Кратные модели представляют собой отношение факторов и имеют вид

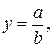(12)

где а, b – факторы (факторные показатели).

Пример:

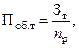(13)

где П_об.т – период одного оборота товаров, дн.; З_т – средний запас товаров; п _р – однодневный объем реализации.

Смешанные модели представляют собой комбинацию перечисленных моделей и могут быть описаны с помощью следующих выражений:

у = (а + b)/ c,(14)

y = a /(b + c),(15)

y = (a · b)/ c,(16)

y = (a + b) · c. (17)

Примером смешанной модели является формула расчета ин­тегрального показателя рентабельности:

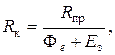(18)

где R _к–рентабельность капитала; R _пр –рентабельность продаж; Ф_е –фондоемкость основных средств; Е _з –коэффициент закрепления оборотных средств.

Однако не любое математическое выражение может являться факторной моделью. Нельзя путать формулу расчета показателя с моделью, отражающей причинно-следственные связи. Например, выработка как показатель производительности труда рассчитывается делением выручки от реализации на среднесписочную численность работников (В = V_р /Ч). Однако это выражение не является моделью, т. к. не отражает причинно следственные связи (рост объема реализации не является фактором увеличения производительности труда, равно как и простое сокращение штата не ведет непосредственно к увеличению производительности труда).