В общем виде детерминированную модель можно представить в виде функции нескольких переменных:
y = f (x 1, x 2, …, xi, …, xn). (19)
Задача детерминированного факторного анализа заключается в определении или количественной оценке влияния каждого фактора на результативный показатель.
Способ цепных подстановок. Он заключается в определении ряда промежуточных значений результативного (обобщающего) показателя путем последовательной замены базисных значений факторов на отчетные. Разность промежуточных значений равна изменению результативного показателя за счет заменяемого фактора. В общем виде способ цепных подстановок имеет вид:
у 0 = а 0 · b 0 · c 0; (20)
у 1* = а 1 · b 0 · c 0; (21)
у 2* = а 1 · b 1 · c 0; (22)
у 1 = а 1 · b 1 · c 1, (23)
где у – обобщающий (результативный) показатель; у 0 – плановое значение результативного показателя; у 1 – фактическое значение результативного показателя; а 0, b 0, с 0 – плановые (базисные) значения факторов, оказывающих влияние на обобщающий (результативный) показатель у; а 1, b 1, с 1 – фактические значения факторов; y 1*, у 2* –1-е и 2-епромежуточные значения результативного показателя.
Общее изменение результата ∆y = у 1 – у 0 складывается из суммы изменений результативного показателя за счет изменения каждого фактора при фиксированных остальных факторах, т. е. ∆y = ∑∆у (а, b, с).
Число расчетов результативного показателя на единицу больше числа измеряемых факторов.
Преимущества данного способа: универсальность применения (применяется в анализе любых типов моделей); простота применения.
Недостаток: в зависимости от выбранного порядка замены факторов результаты факторного разложения имеют разные значения.
Правила, определяющие последовательность подстановки:
- при наличии в факторной модели количественных и качественных показателей в первую очередь производится подстановка количественных факторов;
- если модель представлена несколькими количественными или качественными показателями, последовательность подстановки определяется путем логического анализа.
Пример. Провести анализ влияния количества работников и их выработки на объем выпуска продукции. Зависимость объема выпуска продукции от среднегодовой численности персонала и выработки описывается двухфакторной моделью:
ВП = Ч ∙ В. (24)
Численная реализация алгоритма расчета (по данным табл. 16) представляет собой третий этап факторного анализа:
ВП0 = Ч0 · В0 = 15 · 320 = 4 800 тыс. руб. – базисная величина;
ВП* = Ч1 · В0 = 16 · 320 = 5 120 тыс. руб. – промежуточное (условное) значение;
ВП1 = Ч1 · В1 = 16 · 370 = 5 920 тыс. руб. – отчетная величина.
Изменение объема выпуска продукции из-за изменения численности персонала составит
∆ВП(Ч) = 5 120 – 4 800 = +320 тыс. руб.
Изменения объема выпуска продукции из-за роста выработки:
∆ВП(В) = 5 920 – 5 120 = +800 тыс. руб.
Таблица 16
Показатели, определяющие объем выпуска продукции
| Показатель | Базисный период (0) | Отчетный период (1) | Абсолютное отклонение |
| Объем выпуска продукции (ВП), тыс. руб. | 4 800 | 5 920 | + 1 120 |
| Среднесписочная численность персонала (Ч), чел. | + 1 | ||
| Выработка на одного работника (В), тыс. руб. | + 50 |
Совокупное влияние факторов равно сумме влияний:
∆ВП = ВП(Ч) + ∆ВП(В) = 320 + 800 = 1 120 тыс. руб.
Алгебраическая сумма влияния факторов должна быть равна приросту результативного показателя. Отсутствие такого равенства свидетельствует о допущенных ошибках в расчетах. Результаты расчетов оформляются таблицей (табл. 17). Это особенно важно, если модель многофакторная, а также в том случае, если изучается влияние факторов второго, третьего и т. д. порядков.
Таблица 17
Результаты расчета
| Фактор | Размер влияния, тыс. руб. | Удельный вес влияния, % |
| Среднесписочная численность персонала | 28,60 | |
| Выработка | 71,40 | |
| ИТОГО | 100,00 |
Удельный вес влияния каждого фактора рассчитывается как отношение влияния каждого фактора к совокупному отклонению.
По проведенному расчету можно сделать вывод (реализация четвертого этапа факторного анализа). Выпуск продукции в отчетном периоде по сравнению с базисным возрос на 1 120 тыс. руб., в том числе за счет увеличения среднесписочной численности персонала – на 320 тыс. руб., за счет роста выработки – на 800 тыс. руб. Прирост объема выпуска продукции на 71,40 % обеспечен ростом качественного показателя – производительности труда и на 28,60 % – дополнительным привлечением работников. Таким образом, прирост выпуска продукции объясняется в основном факторами интенсивного развития.
Количество расчетов может быть несколько сокращено, если использовать модификацию способа цепной подстановки способ абсолютных разниц.
Способ абсолютных разниц. Алгоритм решения трехфакторной мультипликативной модели методом цепной подстановки описывается следующим образом:
(20) и (21) → ∆ y (а) = у 1* – у 0= (а 1 – а 0) b 0 · c 0 = ∆ а · b 0 · c 0; (25)
(21) и (22) → ∆ y (b) = у 2* – у 1* = а 1(b 1 – b 0) · c 0 = а 1 · ∆ b · c 0;(26)
(22) и (23) →∆ y (с) = у 1 – у 2* = а 1 · b 1(с 1 – с 0) = а 1 · b 1 · ∆ c. (27)
Следовательно, изменение результативного показателя за счет каждого фактора способом разниц определяется как произведение отклонения изучаемого фактора на базисное или отчетное значение другого (других) факторов в зависимости от выбранной последовательности подстановки.
Пример:
∆ N (Ч) = ∆Ч · В0 = 1 · 320 = +320 тыс. руб.;
∆N (B) = ∆В · Ч1 = 50 · 16 = +800 тыс. руб.
ИТОГО: +1 120 тыс. руб.
Как выше отмечено, изменение последовательности подстановки дает другие результаты расчетов. Если в нашем примере сначала рассчитывать влияние выработки, затем влияние численности персонала, то изменение объема выпуска продукции за счет каждого фактора составит:
∆ N (В) = ∆В · Ч0 = +50 · 15 = 750 тыс. руб.;
∆ N (Ч) = ∆Ч · В1 = +1 · 370 = 370 тыс. руб.
ИТОГО: 1 120 тыс. руб.
Изменение последовательности подстановки выявляет разницу в расчетах, называемую неразложимым остатком, который в данном случае составит 50 тыс. руб.
Для распределения между факторами неразложимого остатка, который при способе цепной подстановки прибавляется к размеру влияния качественного фактора, используют следующие приемы: простое прибавление неразложимого остатка и прием взвешенных конечных разностей.
Прием простого прибавления неразложимого остатка предполагает деление неразложимого остатка на 2 и прибавление результата к величине влияния качественного и количественного факторов.
Формулы определения влияния факторов принимают вид:
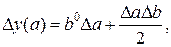 (28)
(28)
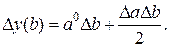 (29)
(29)
Остаточный член в линейном разложении функции y = a · b равен ∆ a · ∆ b.
Но данный способ расчета неприменим при количестве факторов больше двух. В случае большего количества факторов в факторной модели применяется прием взвешенных конечных разностей. Суть его: величина влияния каждого фактора определяется по всем возможным подстановкам, затем результат суммируется и от полученной суммы берется средняя величина.
Пример:
∆ N 1(Ч) = +1 · 370 = 370 тыс. руб.; ∆ N 2(Ч) = +1 · 320 = +320 тыс. руб.;
→ ∆ N ср = (370 + 320)/2 = 345 тыс. руб.;
∆ N 1(В) = +50 · 15 = 750 тыс. руб.; ∆ N 2(B) = +50 · 16 = +800 тыс. руб.;
→ ∆N ср = (750 + 800)/2 = 775 тыс. руб.
ИТОГО: 1 120 тыс. руб.
Рассмотренный способ применим для детерминированных моделей с любым количеством факторов, но он весьма трудоемок, и затраты на его реализацию несопоставимы с выгодами, получаемыми в результате применения.
Пропорциональное распределение остатка по факторам достигается с помощью логарифмического метода.
Способ относительных разниц применяется для измерения размера влияния факторов на изменение результативного показателя только в мультипликативных моделях.
Способ относительных разниц возник в процессе пользования приемом абсолютных разниц. Если абсолютную разницу значений показателя разделить на его базисное значение, то получим относительную разницу. Относительная разница характеризует то, насколько процентов изменилась величина исследуемого фактора.Использование этого способа очень эффективно в случаях, когда исходные данные уже содержат относительные отклонения (темпы изменения) факторных показателей.
Алгоритм расчета величины изменения результативного показателя методом относительных разниц заключается в следующем:
- для расчета размера влияния первого фактора необходимо базисную величину результативного показателя умножить на относительное изменение в процентах первого фактора и результат разделить на 100;
- чтобы рассчитать размер влияния второго фактора, следует к базисной величине результативного показателя прибавить изменение его за счет первого фактора, а затем полученную сумму умножить на относительное изменение в процентах второго фактора и результат разделить на 100;
- чтобы рассчитать размер влияния третьего фактора, необходимо к базисной величине результативного показателя прибавить его изменения за счет первого и второго факторов, а полученную сумму умножить на относительное изменение в процентах третьего фактора и разделить результат на 100;
- влияние последующих факторов находится аналогично.
После завершения расчетов обязательна проверка, которая состоит в сравнении суммарного размера влияний факторов на результативный показатель с величиной его отклонения от базисного значения. Чтобы результаты совпадали, необходимо относительное изменение факторов считать с точностью до сотых или тысячных долей процента.
Этот прием элиминирования по сравнению с другими имеет существенный недостаток. Чтобы определить влияние какого-то фактора, обязательно нужно знать размеры влияния тех факторов, которые в экономической модели стоят перед исследуемым. Тогда как другие приемы элиминирования позволяют определять влияние любого фактора в отдельности. Правда, для этого нужно хорошо знать алгоритм расчетов и иметь определенные навыки факторного анализа.
Пример. Рассмотрим применение этого способа элиминирования на том же примере. Для этого воспользуемся исходной информацией табл. 16. Для удобства таблицу исходных данных дополним информацией об относительных изменениях факторных показателей (табл. 18).
Таблица 18
Исходные данные для расчета влияния трудовых факторов
на выпуск продукции методом относительных разниц
| Показатель | Базисный период (0) | Отчетный период (1) | Темп роста, % | Темп прироста, % |
| Объем выпуска продукции (ВП), тыс. руб. | 4 800 | 5 920 | 123,33 | +23,33 |
| Среднесписочная численность персонала (Ч), чел. | 106,67 | +6,67 | ||
| Выработка на одного работника (В), тыс. руб. | 115,63 | +15,63 |
Объем произведенной продукции, по сравнению с базисным годом, повысился на 1 120 тыс. руб. (5 920 – 4 800).
Факторные показатели (Ч, В) позитивно повлияли на выпуск продукции:
- увеличение среднесписочной численности рабочих:
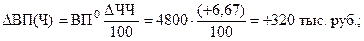
- рост выработки на одного рабочего:
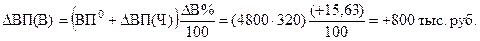
ИТОГО: +1 120 тыс. руб.
После завершения расчетов обязательно выполняется проверка и формулируется вывод. Процедура точно такая же, как и при методе цепных подстановок. Поскольку результаты расчетов совпадают с методом цепных подстановок, выводы не приводим.
Способ процентных разниц. Метод процентных разниц применяется для измерения размера влияния факторов на изменение результативного показателя только в мультипликативных моделях. Метод процентных разниц является разновидностью метода относительных разниц.
Рассмотрим методику расчета влияния факторов этим способом. Для использования этого способа факторного анализа предварительно необходимо исчислить темпы динамики показателей по отношению к их базисным величинам. Напомним, что прием элиминирования исходит из того, что все факторы изменяются независимо друг от друга. Сначала изменяется один, и все другие остаются без изменения, потом изменяются два, затем три и т. д. при неизменности остальных. Это четко прослеживается в данном варианте элиминирования, поскольку, начиная со второго фактора, находится темп динамики показателя, который равен произведению всех впереди стоящих факторов и исследуемого. т. е. второй показатель – это произведение первого и второго фактора, третий – произведение первых трех факторов и т. д. Затем проводится последовательное сравнение темпов динамики (в процентах), т. е. находятся процентные разницы. Для первого фактора темп динамики сравнивается с базисным темпом, который принимается за 100 %. Умножением разности процентов на базисную величину результативного показателя определяют влияние соответствующего фактора на изменение результативного показателя.
Основой применения приема процентных разниц является логическое рассуждение. Если темп динамики первого фактора составил Т процентов, следовательно, величина этого фактора изменилась на (Т – 100) процентов. При прочих равных условиях логично предположить, что и результативный показатель должен был измениться на такое же количество процентов: (Т – 100). Его изменение в абсолютном выражении можно рассчитать, умножив базисное значение результативного показателя на процентное изменение первого фактора и разделив результат на 100. Для нашего примера расчет размера влияния первого фактора (среднесписочной численности рабочих) на изменение выпуска продукции выполняется по формуле
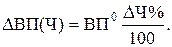 (30)
(30)
Влияние второго фактора находят из предположения, что изменились как первый, так и второй факторы. Поэтому сравнение темпа динамики показателя, равного произведению двух факторов, (Н) и темпа динамики первого фактора (Т) позволяет определить размер влияния (в процентах) второго фактора на изменение результативного показателя. Его изменение в абсолютном выражении под влиянием второго фактора находят умножением этой процентной разницы на базисное значение результативного показателя и делением полученного результата на 100. Если воспользоваться приведенными выше условными обозначениями темпов динамики показателей, то для нашего примера расчет размера влияния второго фактора (выработки на одного рабочего) на изменение выпуска продукции выполняется по формуле
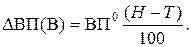 (31)
(31)
Влияние остальных факторов находят аналогично, а сопоставление в процентах ведется по последовательным произведениям нескольких факторов, отражающих их зависимость друг от друга.
После расчетов необходимо выполнить проверку правильности расчетов, т. е. алгебраическая сумма влияния всех факторов обязательно должна совпадать с общим отклонением результативного показателя. Чтобы результаты расчетов сходились, темпы динамики показателей рассчитывают до сотых или тысячных долей процента. После проверки правильности расчетов анализируют полученные результаты.
Покажем на конкретном примере методику расчета методом процентных разниц. Определим влияние численности персонала и выработки на выпуск продукции методом процентных разниц. Для этого используем ту же самую мультипликативную модель (ВП = Ч ∙ В) и исходную информацию табл. 16.
Для удобства вычислений значения необходимых для факторного анализа показателей занесем в табл. 19, в которой выполним все расчеты.
Таблица 19
Расчет влияния среднесписочной численности и выработки
на выпуск продукции методом процентных разниц
| Показатель | Базисный период (0) | Отчетный период (1) | Темп роста, % | Разность процентов, % | Размер влияния фактора, тыс. руб. |
| Среднесписочная численность персонала (Ч), чел. | 106,67 | 106,67 – 100,00 = +6,67 | 4800 ∙ (+6,67/100) = = 320,16 | ||
| Выработка на одного работника (В), тыс. руб. | 115,63 | 115,63 – 106,67 = +8,96 | 4800 · (+8,96/100) = = 430,08 | ||
| Объем выпуска продукции (ВП), тыс. руб. | 123,33 | 123,33 – 115,63 = +7,70 | 4800 · (+7,70/100) = = 369,60 |
Использование метода процентных разниц требует четкого разграничения показателей, используемых для расчетов, и факторов, влияющих на изменение результативного показателя.
Поскольку результаты расчетов совпадают с методом цепных подстановок, проверку и выводы не приводим.
Способ процентных разниц находит широкое применение в практике аналитической работы, поскольку имеет важное преимущество: из учетных данных на предприятии выбирают показатели, которые соответствуют последовательному произведению факторов модели результативного показателя. Поскольку не рассчитываются аналитические факторные показатели (при их расчете возникает необходимость округления результатов), то результаты расчетов по каждому влияющему фактору получаются более точными по сравнению с другими методами элиминирования. Кроме того, это наименее трудоемкий способ расчета из всех рассмотренных. Это ощутимо после приобретения навыков использования разных методов элиминирования.
Логарифмический способ. Достоинство этого способа в том, что он позволяет определить влияние не только двух, но и большего количества факторов на результативный показатель без установления очередности подстановок. Недостатком является то, что данный способ применяется только к мультипликативным моделям, поэтому он не является универсальным. Он основан на логарифмировании отклонения отчетного и базисного значений результативного признака, равного отношению соответствующих произведений факторов.
Результативный показатель можно представить в виде произведения трех факторов:
у = а · b · с. (32)
Прологарифмировав обе части равенства, получим формулу
lg у = lg а + lg b + lg с. (33)
Произведем замену абсолютных значений показателей на индексы:
lg 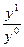 = lg
= lg 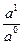 + lg
+ lg 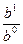 + lg
+ lg 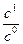 , (34)
, (34)
lg Iу = lg Iа + lg Ib + lg Iс. (35)
Разделив обе части равенства на lg Iy и умножив на ∆ y, получим
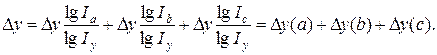 (36)
(36)
Из формулы (36) вытекает, что общий прирост результативного показателя распределяется по факторам пропорционально отношениям логарифмов факторных индексов к логарифму индекса результативного показателя. И не имеет значения, какой логарифм используется – натуральный или десятичный.
Используя данные табл. 16, вычислим прирост объема выпуска продукции за счет двух факторов (ВП = Ч ∙ В).
Изменение объема выпуска продукции из-за изменения численности персонала составит
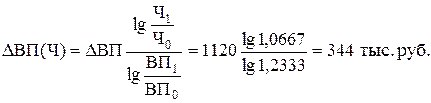
Изменения объема выпуска продукции из-за роста выработки:
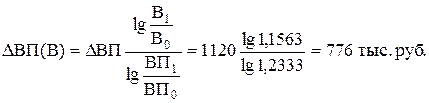
Совокупное влияние факторов равно сумме влияний:
∆ВП = ВП(Ч) + ∆ВП(В) = 344 + 776 = 1 120 тыс. руб.
Способ пропорционального деления. Этот способ применяется к аддитивным и кратно-аддитивным моделям.
Если модель аддитивная: у = а + b + c, то расчет проводится следующим образом:
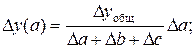 (37)
(37)
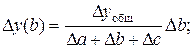 (38)
(38)
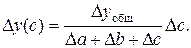 (39)
(39)
Если модель кратно-аддитивная: 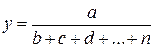 , то расчет значительно усложняется. Взаимосвязь факторов в комбинированной модели представлена на рис. 7.
, то расчет значительно усложняется. Взаимосвязь факторов в комбинированной модели представлена на рис. 7.

Рис. 7. Схема взаимосвязи факторов
Если известны ∆b (d), ∆b (n)и ∆b (m),а также ∆у (b), то для определения ∆у (d), ∆у (n), ∆у (m) можно использовать способ пропорционального деления, который основан на пропорциональном распределении прироста результативного показателя у за счет изменения фактора b между факторами второго уровня d, n, m соответственно величине их прироста. Пропорциональность этого распределения достигается путем определения постоянного для всех факторов коэффициента, который показывает величину изменения результативного показателя y за счет изменения фактора b на единицу.
Величина коэффициента (K)определяется по формуле
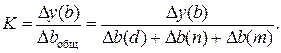 (40)
(40)
Если умножить этот коэффициент на абсолютное отклонение b за счет соответствующего фактора, то найдем изменение результативного показателя:
∆ у (d) = K ∙ ∆ b (d),(41)
∆ у (n) = K ∙ ∆ b (n),(42)
∆ у (m) = K ∙ ∆ b (m).(43)
Способ долевого участия. Этот способ заключается в определении доли каждого фактора в общей сумме их приростов, которая затем умножается на общий прирост результативного показателя. Этот метод применяется к аддитивным и кратно-аддитивным моделям и чаще всего для оценки влияния факторов второго или третьего порядков.
Изменения результативного показателя рассчитываются по формулам:
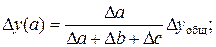 (44)
(44)
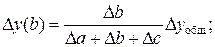 (45)
(45)
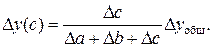 (46)
(46)
Интегральный способ. Этот способ позволяет избежать недостатков, присущих методу цепной подстановки, и не требует применения приемов по распределению неразложимого остатка по факторам, т. к. в нем действует логарифмический закон перераспределения факторных нагрузок.
Интегральный метод позволяет достигнуть полного разложения отклонения результативного показателя по факторам и носит универсальный характер, т. е. применим к мультипликативным, кратным и смешанным моделям. Приведем основные расчетные формулы для различных типов моделей.
Модель типа y = а · b:
∆ y (а) = ∆ а · b 0 + ½∆ а ∆ b; (47)
∆ y (b) = ∆ b · а 0 + ½∆ а ∆ b. (48)
Модель типа y = а · b · c:
∆ y (а) = ½∆ а (b 0 с 1 + b 1 с 0) + ⅓∆ а ∆ b ∆ с; (49)
∆ y (b) = ½∆ b (a 0 с 1 + a 1 с 0) + ⅓∆ а ∆ b ∆ с;(50)
∆ y (с) = ½∆ c (a 0 b 1 + a 1 b 0) + ⅓∆ а ∆ b ∆ с. (51)
Модель типа 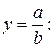
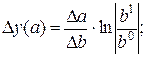 (52)
(52)
Δ y (b) = Δ y – Δ y (a). (53)
Модель типа 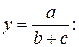
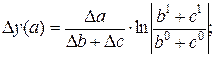 (54)
(54)
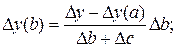 (55)
(55)
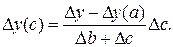 (56)
(56)
Индексный способ. Он основан на построении факторных (агрегированных) индексов. Применение агрегированных индексов означает последовательное элиминирование влияния отдельных факторов на совокупный показатель.
Преимущество: он позволяет произвести «разложение» по факторам не только абсолютное изменение показателя, но и относительное, что особенно важно при изучении факторных динамических моделей:
∆ y (а) = (Iа – 1) · 100 %; (57)
∆ y (b) = (Iy – Iа) · 100 %; (58)
I = Факт/План. (59)
Проверка:
∆ y = ∑∆ у (а, b, у); (60)
∆ y = Iу ∙100 – 100. (61)
Возможность использования основных способов детерминированного факторного анализа приведена в табл. 20.
Таблица 20
Сферы применения способов детерминированного факторного анализа
| Способы | Типы моделей | |||
| аддитивные | мультипликативные | кратные | смешанные | |
| Цепной подстановки | + | + | + | + |
| Абсолютных разниц | – | + | – | у = а (b – с) |
| Относительных и процентных разниц | – | + | – | – |
| Интегральный | – | + | + | у = а /∑ хi |
| Логарифмический | – | + | – | – |
| Индексный | – | + | + | – |
| Пропорционального деления и долевого участия | + | – | – | у = а /∑ хi |
В приложении А представлены основные рабочие формулы расчета влияния изменения факторов на изменение результативного показателя.
Вопросы для самоконтроля
1. По каким признакам классифицируются факторы в экономическом анализе?
2. Приведите примеры интенсивных и экстенсивных факторов, факторов первого, второго и третьего порядков.
3. Что такое детерминированный факторный анализ?
4. Какие существуют свойства детерминированного подхода к анализу?
5. Последовательность проведения детерминированного факторного анализа.
6. Перечислите типы детерминированных моделей, объясните способы их построения.
7. Опишите алгоритмы применения способов детерминированного факторного анализа.
 2015-04-08
2015-04-08 5145
5145
