1) Построить область интегрирования
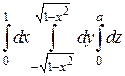
2) Перейти к цилиндрическим координатам,
3) Вычислить данный интеграл
2.6.2. Тройной интеграл в сферической системе координат
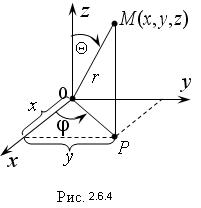 Положение точки в сферической системе координат определяют тремя числами:
Положение точки в сферической системе координат определяют тремя числами:
r – расстоянием до начала координат или длиной радиус-вектора,
Θ – углом между радиус-вектором и осью Oz,
φ – углом между осью Оx и проекцией радиус-вектора на плоскость xOy (Рис. 2.6.4).
Таким образом, координатами точки в сферической системе отсчета являются:
M (r, Θ, φ)
Причем 0 ≤ φ ≤ 2π, 0 ≤ Θ ≤ π.
Найдем связь между декартовыми и сферическими координатами точки М:
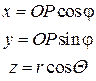
Проекция радиус-вектора на плоскость xOy равна OP = r sinΘ, поэтому
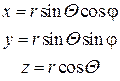 (2.6.6)
(2.6.6)
Перейдем в тройном интеграле от декартовой к сферической системе координат. Для этого вычислим Якобиан.
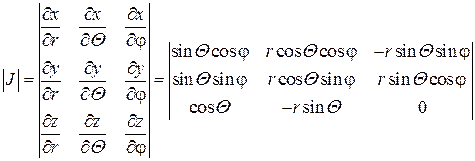
Раскроем определитель по элементам третьей строчки:
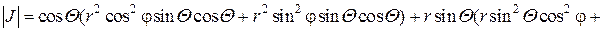
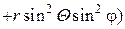
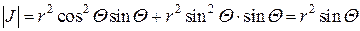
Таким образом, при переходе к сферическим координатам, элемент объема следует преобразовать по формуле:
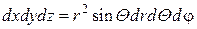 (2.6.7)
(2.6.7)
Подставляя в тройном интеграле вместо переменных x,y,z их выражения через r, Θ, φ из равенств (2.6.6), а вместо dxdydz элемент объема в сферической системе координат (2.6.7), получим:
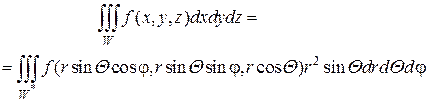 (2.6.8)
(2.6.8)
Переход к сферическим координатам значительно облегчает вычисление тройного интеграла, когда область интегрирования представляет собой шар с центром в начале координат или шаровой слой.
Пример 1. Вычислить тройной интеграл 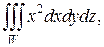 где областью W является сфера радиуса R (Рис. 2.6.5).
где областью W является сфера радиуса R (Рис. 2.6.5).
Решение. Преобразуем тройной интеграл к сферическим координатам:
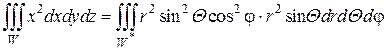
Значения новых переменных r,Θ,φ заключены в пределах:
0 ≤ r ≤ R; 0 ≤ φ ≤ 2π; 0 ≤ Θ < π.
Так как пределы у всех переменных постоянны, можно записать:
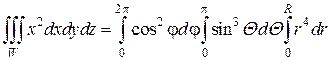
Вычисляя три линейных интеграла, получим:
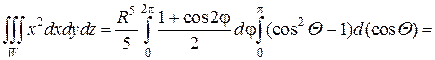
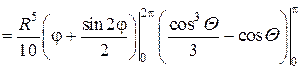
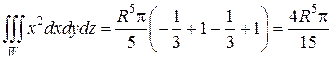
В заключении хотелось бы еще раз подчеркнуть, что замена переменных в кратных интегралах, а именно переход к полярным и цилиндрическим координатам, значительно упрощает вычисление двойных и тройных интегралов, когда плоская область D является частью круга или кольца, а объемная W – проектируется на одну из координатных плоскостей в часть круга или кольца с центром в начале координат.
Точно также переход к сферическим координатам упрощает вычисление тройных интегралов по пространственным областям W, которые представляют собой сферу или часть сферы с центром в начале координат. Если цент смещен, то во всех случаях пределы у внутренних интегралов становятся переменными.
Задача для самостоятельного решения. Вычислить
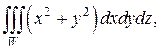
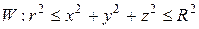 ;
; 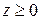
Практическое занятие 2.7 Приложение линейного интеграла к решению геометрических задач
2.7.1. Вычисление площадей плоских фигур
Площадь плоских фигур произвольной формы можно находить по-разному. Начнем с задач о вычислении площадей с помощью линейного интеграла.
1. Система декартовых координат. Пусть фигура ограничена линиями, уравнения которых заданы функциями 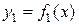 и
и 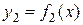 (рис. 2.7.1).
(рис. 2.7.1).
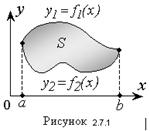 Геометрически линейный определенный интеграл от функции
Геометрически линейный определенный интеграл от функции 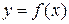 (в предположении, что y ≥ 0) равен площади криволинейной трапеции, ограниченной сверху графиком
(в предположении, что y ≥ 0) равен площади криволинейной трапеции, ограниченной сверху графиком 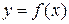 , отрезком [ α,b ] оси Oх и прямыми
, отрезком [ α,b ] оси Oх и прямыми
x = α, x = b, т.е.:
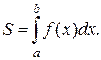
Исходя из этого, площадь фигур любой формы всегда можно представить как, сумму или разность площадей нескольких криволинейных трапеций. В частности, площадь фигуры, изображенной на рисунке 2.7.1, будет равна:
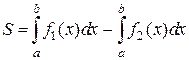
Где числа α и b являются координатой x для точек пересечения линий 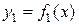 и
и 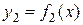
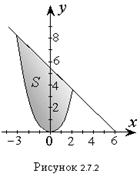
Пример 1. Найти площадь фигуры, ограниченной линиями:
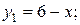
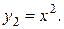
Решение. Графики функций 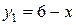 и
и 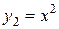 изображены на рисунке 2.7.2. Найдем координату х для точек пересечения из условия:
изображены на рисунке 2.7.2. Найдем координату х для точек пересечения из условия: 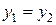
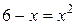
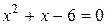
Решая квадратное уравнение, получим:
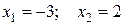
Искомая площадь S равна разности площадей двух криволинейных трапеций, ограниченных снизу отрезком [-3,2] оси Oх, а сверху графиками функций 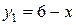 ,
, 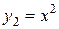 :
:
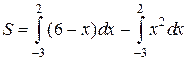
Вычисляя линейные интегралы, найдем
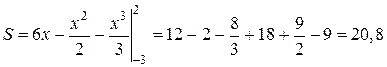 кв.ед.
кв.ед.
2. Если линия 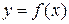 задана параметрическими уравнениями
задана параметрическими уравнениями
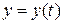 ;
; 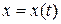 ,
,
то площадь криволинейной трапеции находят с помощью линейного интеграла, совершая в нем замену переменной интегрирования по формуле:
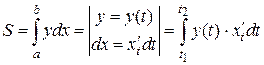
где 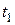 и
и 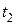 – значения, между которыми изменяется параметр t. Эти значения определяют из уравнений
– значения, между которыми изменяется параметр t. Эти значения определяют из уравнений 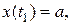
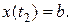
Пример 2. Вычислить площадь, ограниченную астроидой, уравнение которой задано параметрически: 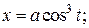
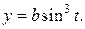
Решение. График астроиды симметричен относительно координатных осей Ox и Oy (рис. 2.7.3). Поэтому искомая площадь равна:
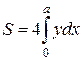
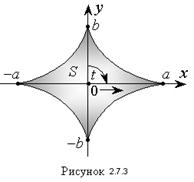 Найдем пределы изменения параметра t, когда переменная x пробегает значения от 0 до а.
Найдем пределы изменения параметра t, когда переменная x пробегает значения от 0 до а.
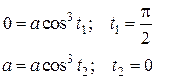
Заменим в линейном интеграле y и dx их выражениями через параметр t из уравнения астроиды. С учетом найденных пределов для t, получим:
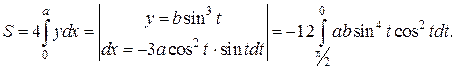
Преобразуем, подынтегральное выражение и поменяем местами верхний и нижний пределы:
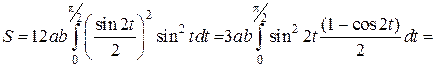
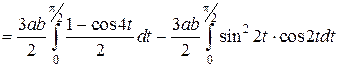
Вычисление последних интегралов дает
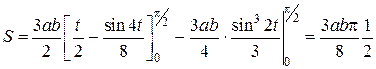 кв.ед.
кв.ед.
3. Система полярных координат. Если линия, ограничивающая плоскую фигуру, задана уравнением в полярной системе координат 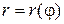 , то вместо площади криволинейной трапеции берут площадь криволинейного сектора. Криволинейным сектором называют фигуру, ограниченную графиком функции
, то вместо площади криволинейной трапеции берут площадь криволинейного сектора. Криволинейным сектором называют фигуру, ограниченную графиком функции 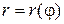 и двумя лучами, проведенными из полюса до пересечения с линией
и двумя лучами, проведенными из полюса до пересечения с линией 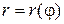 . (Рис. 2.7.4)
. (Рис. 2.7.4)
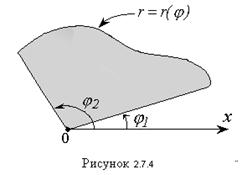
Лучи образуют с полярной осью углы 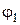 и
и 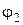 . Площадь такого сектора выражают одним линейным интегралом.
. Площадь такого сектора выражают одним линейным интегралом.
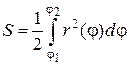
Пусть фигура произвольной формы (Рис.2.7.5), ограничена линиями, уравнения которых заданы в полярной системе координат: 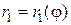 и
и 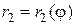 .
.
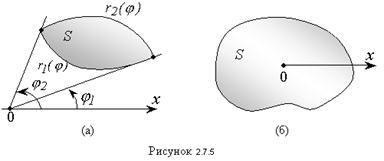
Очевидно, что ее площадь можно представить как разность площадей двух криволинейных секторов, ограниченных графиками функций 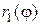 и
и 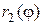 :
:
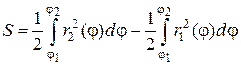
Пределы интегрирования 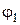 и
и 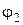 являются полярными углами для точек пересечения линий
являются полярными углами для точек пересечения линий 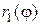 и
и 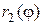 . Эти пределы находят из условия
. Эти пределы находят из условия 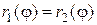 .
.
Если полюс лежит внутри фигуры (Рис. 2.7.5), то полярный угол φ будет изменяться от 0 до 2 π.
Пример 3. Вычислить площадь, ограниченную кардиоидой
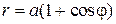
Решение. График кардиоиды, рисунок 2.7.6, симметричен  относительно полярной оси. Поэтому можно найти половину площади, заключенной внутри кардиоиды, а затем удвоить ее. Тогда полярный угол φ будет изменяться от 0 до π. Воспользуемся формулой для площади криволинейного сектора:
относительно полярной оси. Поэтому можно найти половину площади, заключенной внутри кардиоиды, а затем удвоить ее. Тогда полярный угол φ будет изменяться от 0 до π. Воспользуемся формулой для площади криволинейного сектора:
|
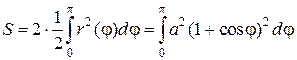
Преобразуем подынтегральное выражение и найдем первообразную
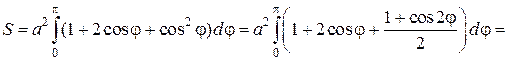
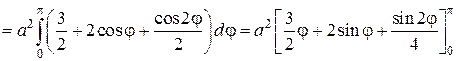
Подставляя верхний и нижний пределы, окончательно получим:
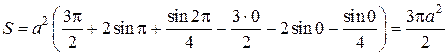
Задачи для самостоятельного решения. Найти площадь фигуры, ограниченной линиями
1. 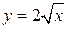 ;
; 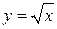 ;
; 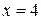 .
.
2. x = 2; y = х; 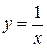 .
.
3. 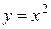 ;
; 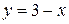 .
.
4. 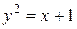 ,
, 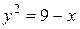 .
.
5. 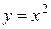 ;
; 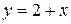 .
.
6. 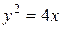 ;
; 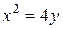 .
.
7. 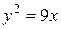 ;
; 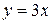 .
.
8. 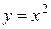 ;
; 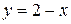 .
.
9. 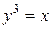 ; x =1;
; x =1; 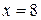 ;
; 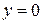 .
.
10. 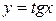 ;
; 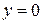 ;
; 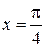 .
.
11. 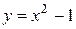 ;
; 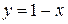 .
.
12. 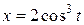 ;
; 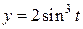 (астроида).
(астроида).
13. 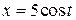 ;
; 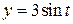 (эллипс).
(эллипс).
14. 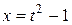 ;
; 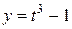
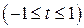 .
.
2.7.2. Вычисление длин линий
Длину плоских кривых, заключенных между двумя точками А и В, можно найти с помощью криволинейного интеграла 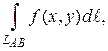 если положить
если положить 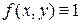 . В этом случае криволинейный интеграл, будет равен размерам области интегрирования, т.е. длине части линии LAB.
. В этом случае криволинейный интеграл, будет равен размерам области интегрирования, т.е. длине части линии LAB.
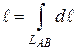
Переходя к линейному интегралу, дает следующие формулы для вычисления длины линии. Если кривая LAB задана в декартовой системе координат непрерывной и дифференцируемой функцией 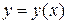 , то вычисление ее длины сводят к вычислению линейного интеграла вида:
, то вычисление ее длины сводят к вычислению линейного интеграла вида:

Пределы в линейном интеграле α и b – являются проекциями на ось Oх точек линии А и В соответственно.
Длину дуги АВ кривой, заданной параметрическими уравнениями 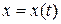 ;
; 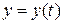 , находят по формуле
, находят по формуле
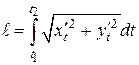
где 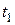 и
и 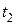 значения параметра t в точках А и В.
значения параметра t в точках А и В.
И наконец, длина линии LAB, уравнение которой 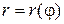 задано в полярной системе координат, равна линейному интегралу
задано в полярной системе координат, равна линейному интегралу
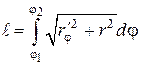
где 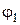 и
и 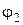 полярные углы точек А и В.
полярные углы точек А и В.
Пример 4. Найти длину полукубической параболы 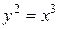 от точки А (0,0) до точки В (4,8).
от точки А (0,0) до точки В (4,8).
Решение. Длина отрезка полукубической параболы между точками А и В равна криволинейному интегралу
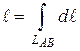
Дифференциал длины кривой в декартовой системе координат выражают через ее уравнение 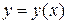 по формуле
по формуле
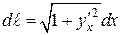
Найдем его для данной линии 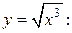
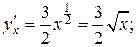
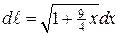
Переход от криволинейного интеграла к линейному и вычисление последнего дает искомую длину:
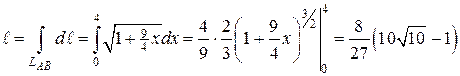 лин.ед.
лин.ед.
Пример 5. Найти длину одной арки циклоиды:
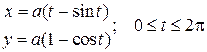
Решение. Выражение для дифференциала длины циклоиды через ее уравнение получено, в лекции 3.9 а, он равен
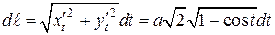
Длину одной арки циклоиды найдем путем перехода к линейному интегралу
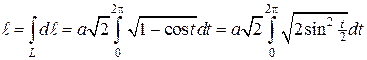
Вычисляя линейный интеграл, получим:
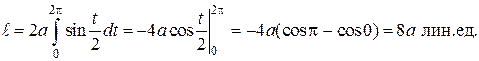
Длина циклоиды равна восьми радиусам воспроизводящей ее окружности. Приведем еще один пример на вычисление длины известной линии, уравнение которой задано в полярной системе координат.
Пример 6. Найти длину кардиоиды 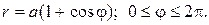
Решение. В примере 3 настоящего параграфа мы нашли площадь, ограниченную кардиоидой, график которой приведен на рисунке 2.7.6.
Чтобы найти длину кардиоиды, выразим дифференциал длины dℓ через ее уравнение
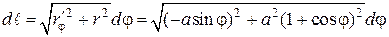
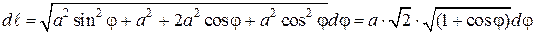
Как уже отмечалось, график кардиоиды симметричен относительно полярной оси, поэтому можно найти половину длины, а затем удвоить ее, тогда полярный угол будет изменяться от 0 до π.
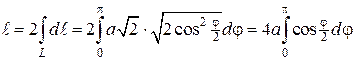
Вычисление последнего интеграла дает
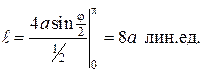
Задачи для самостоятельного решения. Найти длины линий, заданные уравнениями
1. 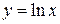 ;
; 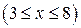
2. 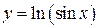 ;
; 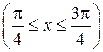
3. 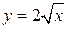 ;
; 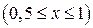
4. 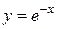 ;
; 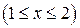
5. 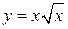 ;
; 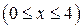
6. 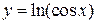 ;
; 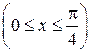
7. 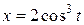 ;
; 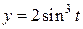
8. 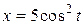 ;
; 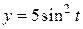 ;
; 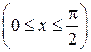
9. 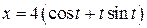 ;
; 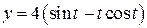 ;
; 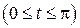
10. 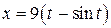 ;
; 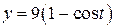 ;
; 
11. 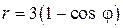
12. 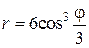 ;
; 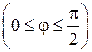
13. 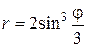 ;
; 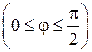
14. 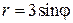
15. 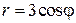
2.7.3. Вычисление объемов тел
Объем тел, в зависимости от их формы и условий задачи, можно находить различными способами.
В частом случае, когда известна площадь поперечных сечений тела, его объем вычисляют с помощью линейного интеграла по формуле:
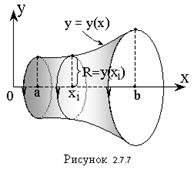
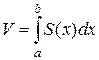
где S(x) – площадь сечения тела плоскостью, перпендикулярной оси Ox, α и b – проекции его крайних точек на ту же ось.
Исходя из этой формулы, находят объем тел вращения.
Пусть криволинейная трапеция, ограниченная сверху графиком непрерывной функции y = y(x) и прямыми x = α, x = b, вращается вокруг оси Oх (Рис. 2.7.7).
В результате ее вращения образуется тело. Его плоскими сечениями, перпендикулярными оси Oх, являются круги с различными радиусами R=y(x), площадь которых равна:
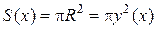
 Следовательно, объем полученного тела можно найти по формуле
Следовательно, объем полученного тела можно найти по формуле
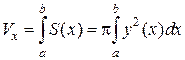
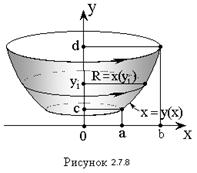
При вращении линии, ограничивающей криволинейную трапецию, вокруг оси Oy (Рис. 2.7.8) объем полученного тела равен:
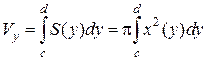
где x(y) – уравнение вращающейся линии решенное относительно переменной x.
Пример 7. Найти объем тела, полученного при вращении эллипса относительно осей Ox и Oy.
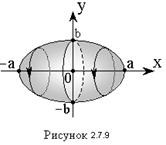 Решение. График эллипса
Решение. График эллипса 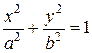 изображен на рисунке 2.7.9.
изображен на рисунке 2.7.9.
Координаты его крайних точек по оси 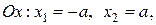
по оси 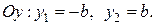
Объем тела, образованного вращением эллипса относительно оси Oх, найдем по формуле:
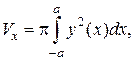 где
где 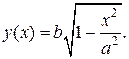
С учетом симметрии
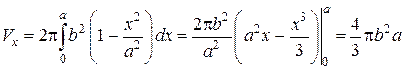
Аналогично, вычислим объем Vy
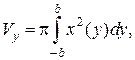 где
где 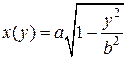
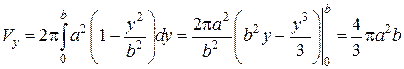
Если α = b, то тела вращения относительно осей Oх и Oy становятся шаром, объем которого равен 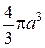 .
.
Задачи для самостоятельного решения. Найти объемы тел вращения
1. 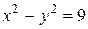 ;
; 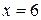 ;
; 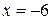 ;
; 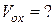
2. 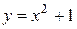 ;
; 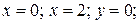
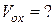
3. 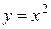 ;
; 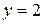 ;
; 
4. 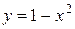 ;
; 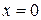 ;
; 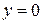 ;
; 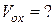
5. 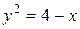 ;
; 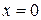 ;
; 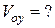
6. 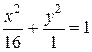 ;
; 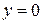 ;
; 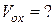
7. 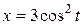 ;
; 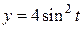 ;
; 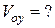
8. 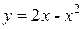 ;
; 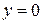 ;
; 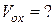
9. 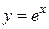 ;
; 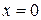 ;
; 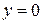 ;
; 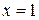 ;
; 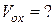
10. 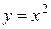 ;
; 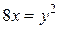 ;
; 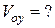
Практическое занятие 2.8. Геометрические приложения кратных интегралов
2.8.1. Вычисление площадей плоских фигур с помощью двойного интеграла
Если в двойном интеграле 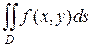 по плоской области D положить
по плоской области D положить 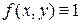 , то он будет равен размерам D, т.е. ее площади:
, то он будет равен размерам D, т.е. ее площади:
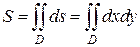
Приведем несколько задач на вычисление площадей с помощью двойного интеграла.
Пример 1. Вычислить площадь, ограниченную параболами 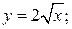
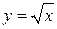 и прямой х = 4.
и прямой х = 4.
Решение. Построим графики ограничивающих линий (рис. 2.8.1). Площадь полученной плоской фигуры равна двойному интегралу:
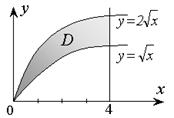 |
| Рис. 2.8.1 |
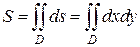
Переход к двукратному интегрированию дает искомую площадь
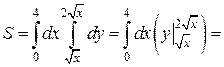
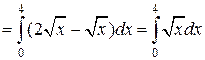
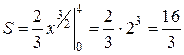 кв.ед.
кв.ед.
Эту же площадь можно найти с помощью линейного интеграла, представив ее как разность площадей двух криволинейных трапеций
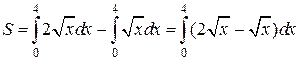
Результаты в обоих случаях одинаковы.
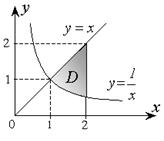
Пример 2. Найти площадь, ограниченную линиями: х = 2; y = x; 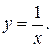
Решение. Плоская фигура, площадь которой нужно найти, изображена на рис. 2.8.2. Искомая площадь равна двойному интегралу:
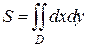
 |
| Рис. 2.8.2 |
Найдем координату x точки пересечения линий y = x и 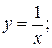
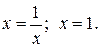
Переменная х внутри области D изменяется от 1 до 2, а переменная y от своих значений на линии 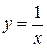 до значений на линии
до значений на линии 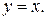 Переходя к последовательному вычислению двух линейных интегралов, получим:
Переходя к последовательному вычислению двух линейных интегралов, получим:
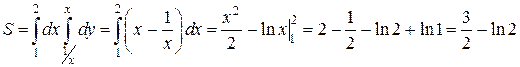
Пример 3. Найти площадь плоской фигуры, ограниченную эллипсом
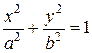
Решение. Площадь области D ( рис. 2.8.3), также найдем с помощью двойного интеграла
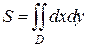
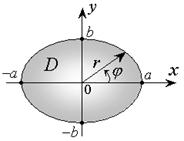 |
| Рис. 2.8.3 |
Для упрощения вычислений перейдем к новым переменным интегрирования r и 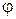 по формуле
по формуле
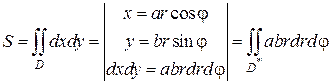
Внутри области D угол φ пробегает значения от 0 до 2 π, а переменная r изменяется от 0 до своих значений на уравнении эллипса. Это уравнение в новой системе отсчета имеет вид:
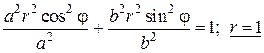
Переходя к двукратному интегрированию, получим
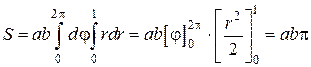 кв.ед.
кв.ед.
Если α = b, то эллипс становится окружностью, площадь которой a 2π.
Задачи для самостоятельного решения. С помощью двойного интеграла найти площадь фигур, ограниченных линиями:
1. 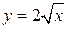 ;
; 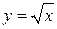 ;
; 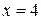 ;
;
2. 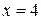 ;
; 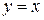 ;
; 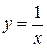 ;
;
3. 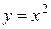 ;
; 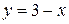 ;
;
4. 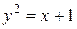 ,
, 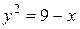 ;
;
5. 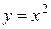 ;
; 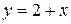 ;
;
6. 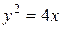 ;
; 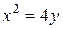 ;
;
7. 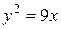 ;
; 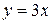 ;
;
8. 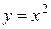 ;
; 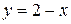 ;
;
9. 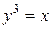 ;
; 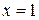 ;
; 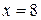 ;
; 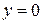 ;
;
10. 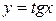 ;
; 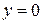 ;
; 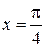 .
.
11. 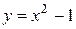 ;
; 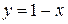 .
.
12. 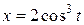 ;
; 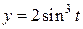 (астроида).
(астроида).
13. 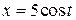 ;
; 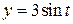 (эллипс).
(эллипс).
14. 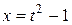 ;
; 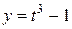
2.8.2. Вычисление объемов тел с помощью двойного и тройного интегралов
Рассмотрим теперь общий случай вычисления объемов тел с помощью кратныx интегралов.
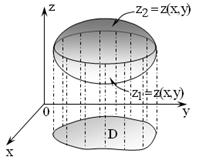 |
| Рис. 2.8.4 |
Пусть тело произвольной формы ограничено двумя поверхностями, уравнения которых известны:
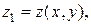
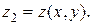
Проекцией данного тела на плоскость xOy является область D (рис. 2.8.4). Двойной интеграл по области D геометрически равен объему цилиндра, построенного на этой области и ограниченного сверху графиком подынтегральной функции. Поэтому объем тела, изображенного на рисунке 2.8.4, можно представить как разность объемов двух цилиндрических тел, или как разность двух двойных интегралов:
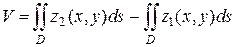
В самом общем случае объем тел произвольной формы находят с помощью тройного интеграла, в котором подынтегральная функция равна единице
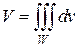
Легко заметить, что предыдущая формула является следствием последней, в самом деле:
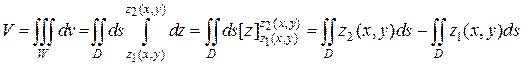
Приведем несколько примеров, связанных с вычислением объемов тел при помощи кратных интегралов.
Пример 4. Найти объем, ограниченный поверхностями:
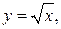
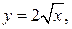 z = 0, z + x = 6
z = 0, z + x = 6
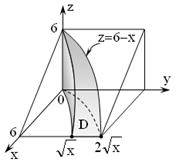 |
| Рис. 2.8.5 |
Решение. Тело ограничено двумя цилиндрическими поверхностями 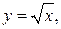
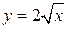 с образующими, параллельными оси Oz, и двумя плоскостями z = 0, z = 6 – x. Искомый объем равен объему цилиндрического тела, построенного на области D и ограниченного сверху плоскостью z = 6 – x (рис. 2.8.5). Найдем его с помощью двойного интеграла
с образующими, параллельными оси Oz, и двумя плоскостями z = 0, z = 6 – x. Искомый объем равен объему цилиндрического тела, построенного на области D и ограниченного сверху плоскостью z = 6 – x (рис. 2.8.5). Найдем его с помощью двойного интеграла
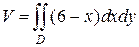
Переменная x внутри области D изменяется от 0 до 6, а переменная y от ее значений на линии 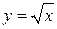 до значений на линии
до значений на линии 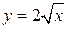 . Перейдем к двукратному интегрированию:
. Перейдем к двукратному интегрированию:
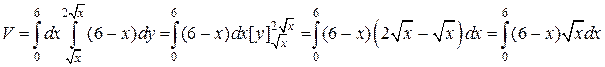
Вычисляя последний интеграл, получим
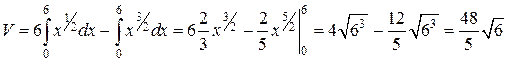 куб.ед.
куб.ед.
Для сравнения найдем этот же объем с помощью тройного интеграла
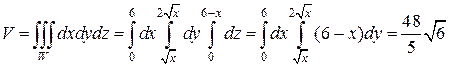 куб.ед.
куб.ед.
После подстановки пределов для переменной z мы приходим к такому же двойному интегралу.
Пример 5. Найти объем тела, ограниченного поверхностями
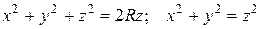
Решение. Данное тело заключено внутри конуса 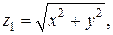 отсеченного сверху сферой
отсеченного сверху сферой 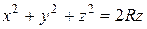 со смещенным центром по оси Oz. Чтобы найти смещение центра и радиус сферы приведем ее уравнение к каноническому виду. Для этого выделим полный квадрат по переменной z:
со смещенным центром по оси Oz. Чтобы найти смещение центра и радиус сферы приведем ее уравнение к каноническому виду. Для этого выделим полный квадрат по переменной z:
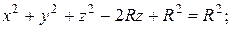
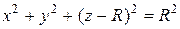
Таким образом, радиус сферы равен R, центр смещен вверх по оси Oz на R единиц (рис. 2.8.7). Уравнение верхней половины сферы, решенное относительно z имеет вид:
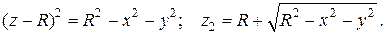
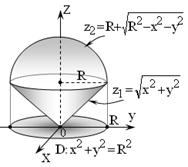 |
| Рис. 2.8.7 |
Конус и сфера пересекаются по окружности. Чтобы определить ее радиус, в уравнении сферы 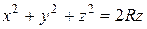 заменим выражение
заменим выражение 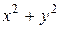 на
на 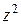 :
:
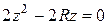
Корни полученного квадратного уравнения равны: z = 0; z = R. Подставляя z = R в любое из уравнений: либо конуса, либо сферы найдем уравнение их линии пересечения: 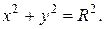
Искомый объем, так же как в предыдущей задаче, вычислим с помощью тройного интеграла
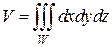 .
.
Тело W проектируется на плоскость xOy в круг с радиусом R. Перейдем к цилиндрическим координатам:
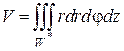
Значения полярного угла φ и полярного радиуса r заключены в пределах
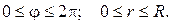
Переменная z внутри данного тела изменяется от своих значений на конусе 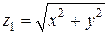 до значений на верхней части сферы
до значений на верхней части сферы 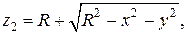 а в цилиндрической системе отсчета от
а в цилиндрической системе отсчета от 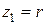 до
до 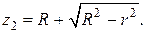 Расставляя пределы изменения для переменных φ, r и z и переходя к трехкратному интегрированию, получим
Расставляя пределы изменения для переменных φ, r и z и переходя к трехкратному интегрированию, получим
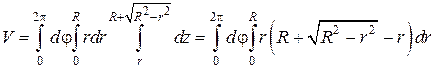
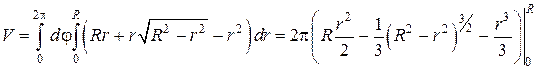
Подстановка верхнего и нижнего пределов для переменной r дает искомый объем:
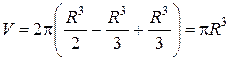 куб. ед
куб. ед
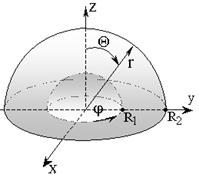
Пример 6. Найти объем области W, заданной неравенствами
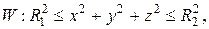
где z ≥0; 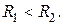
 |
| Рис. 2.8.8 |
Решение. Область W расположена над плоскостью xОy и заключена между двумя полусферами с радиусами 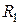 и
и 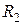 и центром в начале координат (рис. 2.8.8). Ее объем равен тройному интегралу
и центром в начале координат (рис. 2.8.8). Ее объем равен тройному интегралу
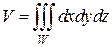
Для упрощения вычислений в данном случае удобно перейти к сферическим координатам
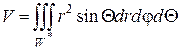
Значения переменных r,φ и Θ внутри области W заключены в пределах
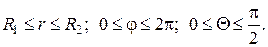
Переходя к трехкратному интегрированию, получим:
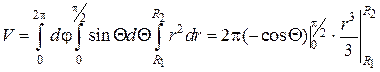
Подстановка пределов дает искомый объем
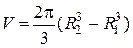 куб.ед.
куб.ед.
Размеры данной области можно найти другим способом. Известно, что объем шара вычисляют по формуле
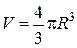
Отсюда, объем половины шарового слоя, заключенного между двумя сферами, равен разности
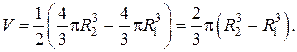
Результат получился тот же самый.
Задачи для самостоятельного решения. Найти объемы тел, ограниченных поверхностями:
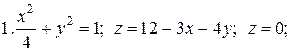
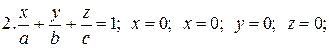
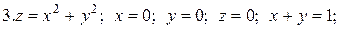
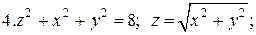
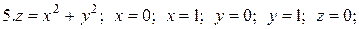
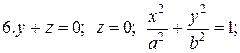
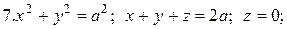
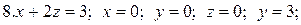
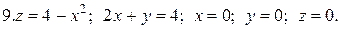
 2015-04-12
2015-04-12 3643
3643