Замена переменных интегрирования х и у в двойном интеграле, часто существенно упрощает его вычисление.
Пусть с помощью функций:
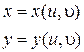 (2.5.1)
(2.5.1)
осуществляют переход от старых координат x, y к новым u, υ.
Эти функции должны быть непрерывными вместе со своими частными производными и однозначно решаться относительно u и υ. При этих условиях область D будет однозначно отображаться в область D *.
При переходе от декартовых к криволинейным координатам элемент площади dxdy преобразуется в элемент площади dudυ при этом они связаны соотношением:
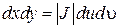 (2.5.2)
(2.5.2)
где 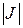 – функциональный определитель Якоби, или Якобиан, он равен:
– функциональный определитель Якоби, или Якобиан, он равен:
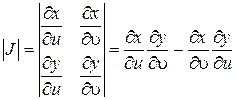
Таким образом, в общем случае замену переменных интегрирования в двойном интеграле осуществляют по формуле:
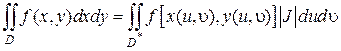 (2.5.3)
(2.5.3)
Из выражения (2.5.3) следует, что для того чтобы в двойном интеграле перейти к новым переменным интегрирования, нужно: переменные x и y заменить функциями (2.5.1), вместо элемента площади ds = dxdy подставить выражение 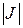 dudυ и область D заменить ее отображением D *. Затем, вычисление двойного интеграла (2.5.3) сводят к последовательному вычислению двух линейных интегралов по новым переменным u и υ.
dudυ и область D заменить ее отображением D *. Затем, вычисление двойного интеграла (2.5.3) сводят к последовательному вычислению двух линейных интегралов по новым переменным u и υ.
Перейдем в двойном интеграле от декартовых к полярным координатам по формуле (2.5.3), при этом за u примем полярный радиус r, а за υ – угол φ:
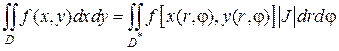
Функции x (r,φ) и y (r, φ) известны, они равны:
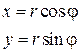
Найдем определитель Якоби:
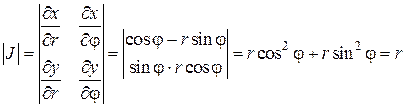
Тогда
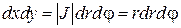 (2.5.4)
(2.5.4)
и двойной интеграл в полярной системе координат примет вид:
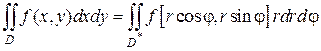 (2.5.5)
(2.5.5)
Чтобы вычислить полученный интеграл (2.5.5), следует перейти к двукратному интегрированию по новым переменным r и φ, а для этого нужно найти пределы их изменения в области D *.
Построение области D * в полярных координатах не обязательно. Если построена область D в декартовой системе координат, то пределы изменения полярного радиуса r и угла φ в новой системе отсчета легко определить по области D.
Например, пусть область D ограничена замкнутой кривой, а полюс лежит внутри кривой (рис. 2.5.1).

В этом случае нужно найти полярное уравнение ограничивающей линии r = r (φ).
Тогда угол φ внутри области будет изменяться от 0 до 2π, а полярный радиус r – от 0 до своих значений на кривой r = r (φ), т.е.:
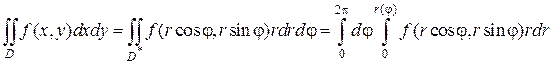
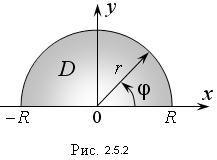
Если область D в декартовой системе отсчета есть полукруг радиуса R с центром в начале координат, расположенный в верхней полуплоскости (рис. 2.5.2), то значения полярного радиуса r и угла φ внутри D заключены в пределах 0 ≤ r ≤ R, 0 ≤ φ ≤ π,
следовательно:
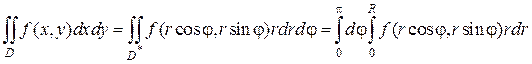
И наконец может быть еще такой случай. Полюс лежит за пределами области D (Рис. 2.5.3), которая ограничена двумя линиями:
r 1 = r 1(φ) и r 2 = r 2(φ),
тогда 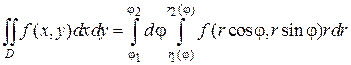
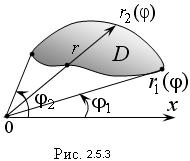
Приведем несколько примеров.
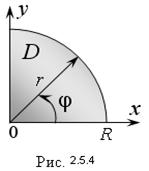 Пример 1. Вычислить двойной интеграл
Пример 1. Вычислить двойной интеграл 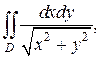 где область D есть первая четверть круга
где область D есть первая четверть круга 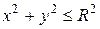 .
.
Решение. Построим область D в декартовой системе координат (рис. 2.5.4). В двойном интеграле перейдем к полярным координатам по формуле (2.5.5):
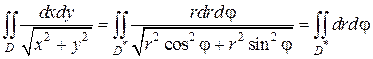
Полярный угол φ в области D изменяется от 0 до 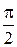 , а полярный радиус r – от 0 до R, следовательно:
, а полярный радиус r – от 0 до R, следовательно:
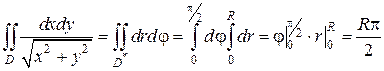
Пример 2. Вычислить двойной интеграл 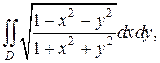 где область D верхняя часть круга
где область D верхняя часть круга 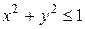 .
.
Решение. Перейдем к полярным координатам в двойном интеграле
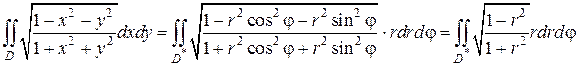
Значения переменных φ и r заключены в пределах 0 ≤ φ ≤ π, 0 ≤ r ≤ 1, поэтому
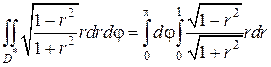
Каждый из линейных интегралов в правой части равенства можно вычислить отдельно, так как пределы постоянны:
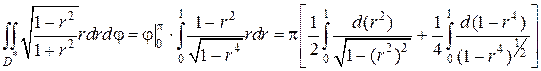
Находя первообразные и подставляя пределы окончательно получим:
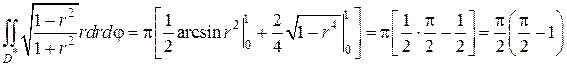
Пример 3. Вычислить двойной интеграл 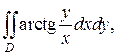
где D есть часть кольца, определяемая неравенствами:
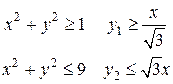
Решение. Построим область D (рис. 2.5.5). Вычисление данного интеграла в декартовой системе координат довольно громоздко, поэтому лучше преобразовать двойной интеграл к полярным координатам:
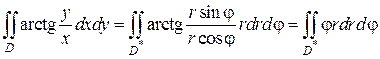
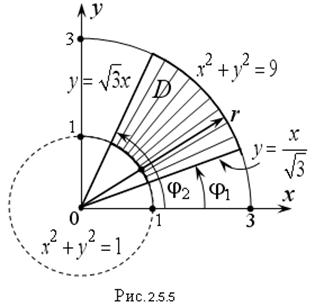
В области D полярный радиус r изменяется от 1 до 3, а полярный угол φ от 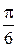 до
до 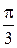 . Переходя к двукратному интегрированию по φ и r, получим:
. Переходя к двукратному интегрированию по φ и r, получим: 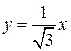 .
.
Примечание. Уравнения окружностей x 2 + y 2 = 1 и x 2 + y 2 = 9 в полярной системе представляют собой координатные линии вида r = 1 и r = 3 соответственно. В этом легко убедиться, если в данные уравнения вместо переменных x и y подставить их выражения через полярные координаты:
x = r ·cosφ, y = r ·sinφ, в самом деле
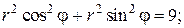
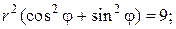 r = 3
r = 3
Уравнения прямых 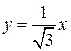 и
и 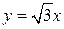 , проходящих через начало координат, в полярной системе также переходят в координатные линии
, проходящих через начало координат, в полярной системе также переходят в координатные линии 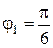 и
и 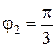 . В частности,
. В частности, 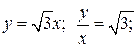
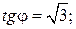
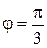 .
.
Пример 4. Вычислить двойной интеграл
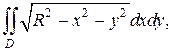
где область интегрирования задана неравенством 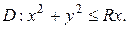
Решение. Преобразуем уравнение 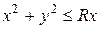 , выделив полный квадрат по переменной x:
, выделив полный квадрат по переменной x:
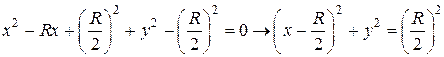
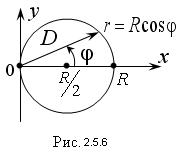
Следовательно, границей области D является окружность радиуса 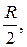 центр которой смещен вправо по оси Ох на величину
центр которой смещен вправо по оси Ох на величину 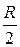 (рис. 2.5.6).
(рис. 2.5.6).
В данном случае также удобно перейти к полярным координатам:
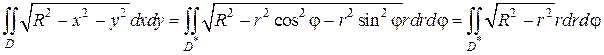
Полярный угол φ будет изменяться от 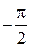 до
до 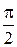 . Чтобы определить пределы для второй переменной r, найдем уравнение окружности в полярной системе:
. Чтобы определить пределы для второй переменной r, найдем уравнение окружности в полярной системе:
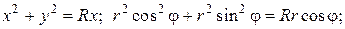
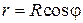
Полярный радиус r внутри области D изменяется от 0 до своих значений на линии r = R cosφ (Рис. 2.5.6), т.е. пределы во внутреннем интеграле зависят от φ. Поэтому интегрируем сначала по r:
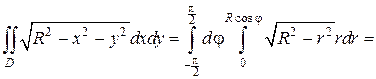
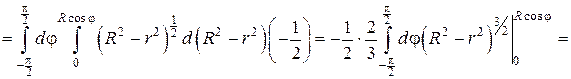
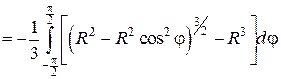
В последнем выражении вынесем за знак интеграла R 3 и учтем, что 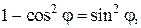 тогда:
тогда:
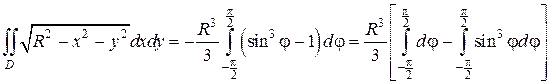
Вычисляя последние интегралы по переменной φ, окончательно получим:
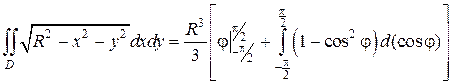
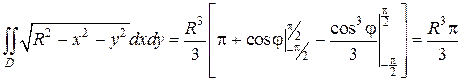
Из приведенных примеров следует, что когда область интегрирования представляет собой круг, кольцо или часть круга и кольца с центром в начале координат, то при переходе к полярной системе, пределы у новых переменных φ и r становятся постоянными, а это значительно упрощает вычисления двойных интегралов.
Задачи для самостоятельного решения. Перейти к полярным координатам в двойном интеграле 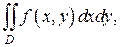 ,
,
Расставить пределы для переменных r и j.
1. 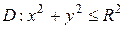
2. 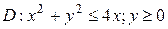
3. 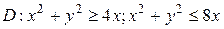
4. Перейти к полярным координатам в интеграле 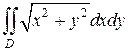 ,
,
расставить пределы, если область D ограничена линиями:
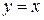 ;
; 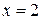 ;
; 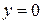
5. 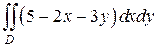 . Перейти к полярным координатам, расставить пределы, если
. Перейти к полярным координатам, расставить пределы, если 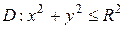
6. Вычислить 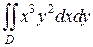 ; D – первая четверть круга
; D – первая четверть круга 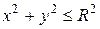 .
.
Практическое занятие 2.6. Тройной интеграл в цилиндрической и сферической системах координат
В общем случае замену переменных интегрирования в тройном интеграле осуществляют так же, как и в двойном.
Пусть функции:
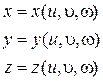 (2.6.1)
(2.6.1)
непрерывны вместе со своими частными производными и однозначно разрешаются относительно u, υ, ω. Тогда, с помощью этих функций область W в декартовой системе координат однозначно отображается в область W * в криволинейной системе координат.
При этом элементы dV и dV * в старой и новой системах будут связаны соотношением:
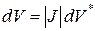 или
или
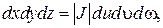 (2.6.2)
(2.6.2)
где
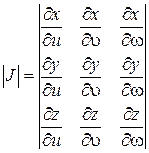
В результате тройной интеграл преобразуется по формуле:
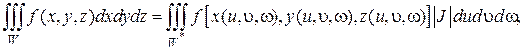 (2.6.3),
(2.6.3),
а его вычисление сводят к трехкратному интегрированию по переменным u, υ, ω. Примерами криволинейных систем в пространстве могут служить цилиндрическая и сферическая системы координат. Перейдем к их рассмотрению.
Тройной интеграл в цилиндрических координатах
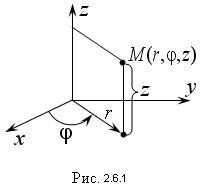
Положение точки в пространстве в цилиндрической системе координат однозначно задают тремя числами φ, r, z.
Цилиндрические координаты точки получают путем добавления к ее полярным координатам аппликаты z (рис. 2.6.1). Цилиндрические и декартовые координаты точки связаны между собой соотношениями:
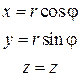 (2.6.4)
(2.6.4)
Перейдем в тройном интеграле от декартовых к цилиндрическим координатам. Элемент объема dV преобразуется по формуле
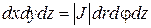
Найдем определитель Якоби:
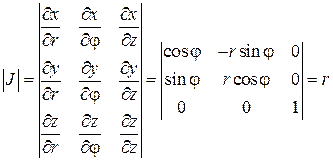
следовательно:
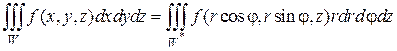 (2.6.5)
(2.6.5)
Далее, нужно перейти к трем линейным интегралам по переменным r,φ, z. Пределы изменения новых переменных расставляют по виду области W. Так же как и в двойном интеграле строить область W * не обязательно. Покажем это на примере.
Пример 1. Вычислить тройной интеграл 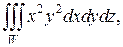 где область W задана неравенствами:
где область W задана неравенствами:
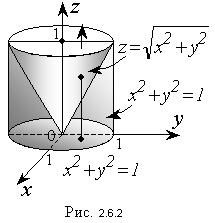
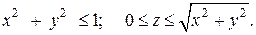
Решение. Область, по которой нужно вычислить тройной интеграл, заключена внутри цилиндра 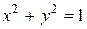 , а сверху отрезана конусом
, а сверху отрезана конусом 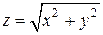 (рис. 2.6.2).
(рис. 2.6.2).
Цилиндрическая поверхность и конус пересекаются по линии 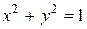 на высоте z =1. Перейдем в тройном интеграле к цилиндрическим координатам по формуле (2.6.5):
на высоте z =1. Перейдем в тройном интеграле к цилиндрическим координатам по формуле (2.6.5):
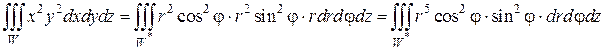
Найдем пределы изменения r,φ, z. Проекция W на плоскость xОy – есть круг, ограниченный окружностью 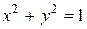 уравнение которой в полярной системе является координатной линией r = 1. Следовательно, значения переменных r и φ заключены в пределах:
уравнение которой в полярной системе является координатной линией r = 1. Следовательно, значения переменных r и φ заключены в пределах:
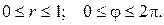
Для определения границ изменения переменной z, проведем прямые, параллельные оси Oz. Эти прямые будут входить в область W на плоскости
z = 0 и выходить из нее на конической поверхности 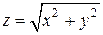 Найдем уравнение этой поверхности в цилиндрической системе
Найдем уравнение этой поверхности в цилиндрической системе
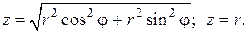
Таким образом, переменная z в области W изменяется от 0 до своих значений на конусе z = r. Переходя к трехкратному интегрированию по переменным r, φ и z, получим:

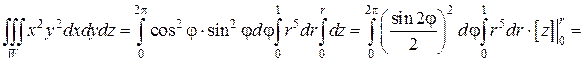
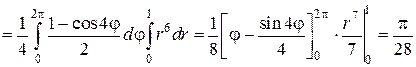
В данном примере проекцией W на плоскость xOy был круг с центром в начале координат, поэтому при переходе к цилиндрическим координатам пределы у переменных r и φ были постоянными. Это упростило вычисление тройного интеграла.
Пример 2. Вычислить тройной интеграл 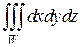 , где область W задана неравенствами
, где область W задана неравенствами 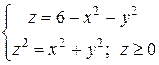
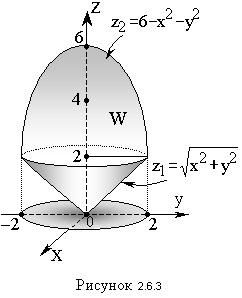
Решение. Область ограничена двумя поверхностями: снизу – конусом 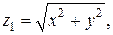 сверху – параболоидом вращения
сверху – параболоидом вращения 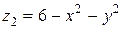 (рис. 2.6.3).
(рис. 2.6.3).
Их линией пересечения является окружность. Найдем ее уравнение из условия 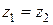 . Для этого в уравнении параболоида заменим выражение
. Для этого в уравнении параболоида заменим выражение 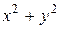 на
на 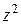 :
:
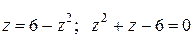
Корни полученного квадратного уравнения раны 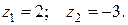
 Подставляя z = 2 в любое из уравнений, либо конуса, либо параболоида вращения, найдем уравнение их линии пересечения:
Подставляя z = 2 в любое из уравнений, либо конуса, либо параболоида вращения, найдем уравнение их линии пересечения:
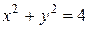
Так как область W проектируется на плоскость xOy в круг с радиусом R = 2, и центром в начале координат, в тройном интеграле перейдем к цилиндрическим координатам:
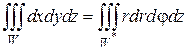
Внутри области W полярный угол φ изменяется от 0 до 2 π, а полярный радиус r – от 0 до 2. Значения переменной z заключены между двумя поверхностями 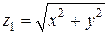 и
и 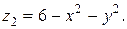
Найдем их уравнения в цилиндрической системе отсчета
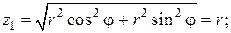
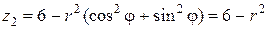
Расставляя пределы изменения для переменных φ, r и z и переходя к трехкратному интегрированию, получим
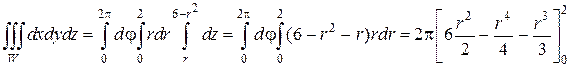
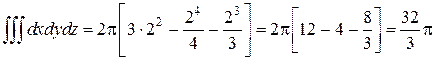
 2015-04-12
2015-04-12 23587
23587
