2 Матрицей называется числовая таблица 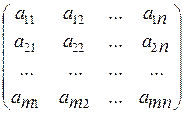 .
.
Числа 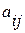 называются элементами матрицы. Индексы i и j означают, соответственно, номер строки и номер столбца, в которых расположен элемент
называются элементами матрицы. Индексы i и j означают, соответственно, номер строки и номер столбца, в которых расположен элемент 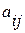 Число строк, умноженное на число столбцов, называется порядком матрицы. Например, матрица
Число строк, умноженное на число столбцов, называется порядком матрицы. Например, матрица 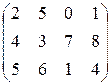 является матрицей порядка 3´4. Если число строк матрицы совпадает с числом столбцов (m = n), то такая матрица называется квадратной (размерности n). В дальнейшем мы будем обозначить матрицы заглавными буквами латинского алфавита (A, B, C, D,…).
является матрицей порядка 3´4. Если число строк матрицы совпадает с числом столбцов (m = n), то такая матрица называется квадратной (размерности n). В дальнейшем мы будем обозначить матрицы заглавными буквами латинского алфавита (A, B, C, D,…).
Элементы квадратной матрицы, идущие из левого верхнего угла матрицы в правый нижний угол, называются главной диагональю матрицы. Элементы квадратной матрицы, идущие из левого нижнего угла матрицы, в правый верхний угол, называются вспомогательной диагональю матрицы. Для квадратных матриц вводится понятие определителя.
2 Определителем матрицы второго порядка называется число, вычисляемое по формуле
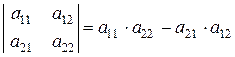 . (1.1)
. (1.1)
То есть, определитель матрицы второго порядка равен произведению элементов главной диагонали матрицы минус произведение элементов вспомогательной диагонали. Определитель матрицы А обозначается вертикальными прямыми 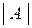 или символом det A.
или символом det A.
Пример 1.1. Вычислить определитель 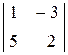 .
.
В соответствие с формулой (1.1) получим:
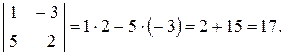
2 Определителем матрицы третьего порядка называется число, вычисляемое по формуле
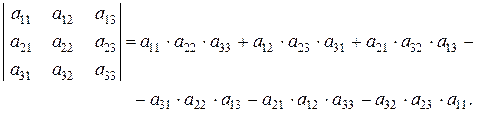 (1.2)
(1.2)
Одним из методов, позволяющих запомнить громоздкую формулу (1.2) является метод треугольников. Первые три слагаемых, стоящих в правой части формулы (1.2), являются произведениями элементов главной диагонали матрицы и треугольников, одна из сторон которых параллельна главной диагонали

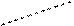

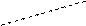

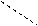

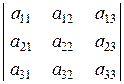 .
.
Последние три слагаемые берутся с противоположным знаком и являются произведениями элементов вспомогательной диагонали матрицы и треугольников, одна из сторон которых параллельна вспомогательной диагонали
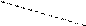

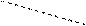


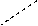

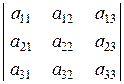 .
.
Пример 1.2. Вычислить определитель третьего порядка: 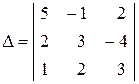 .
.
Вычислим определитель по формуле (1.2). Получим:
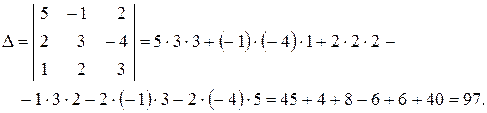
Строгое определение определителя n -го порядка мы приводить не будем, т.к. в нем используется понятие числа инверсий в перестановке, которое нам в дальнейшем не понадобится. Тем не менее, вычислять определители 4-го, 5-го,… порядка мы будем, используя метод разложения определителя по строке или столбцу.
2 Алгебраическим дополнением 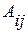 к элементу
к элементу 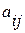 квадратной матрицы А называется число, равное определителю матрицы
квадратной матрицы А называется число, равное определителю матрицы 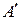 (n – 1)-го порядка, полученной из матрицы А путем вычеркивания i -ой строки и j -го столбца и взятому со знаком плюс, если сумма i+j является четным числом, и со знаком минус, если это число нечетное. Таким образом, алгебраическое дополнение можно найти по формуле:
(n – 1)-го порядка, полученной из матрицы А путем вычеркивания i -ой строки и j -го столбца и взятому со знаком плюс, если сумма i+j является четным числом, и со знаком минус, если это число нечетное. Таким образом, алгебраическое дополнение можно найти по формуле:
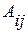 =
= 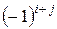 ×det
×det 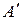 .
.
1 Метод разложения определителя по строке или столбцу. Определитель любого порядка равен сумме произведений элементов какой либо строки или столбца на их алгебраические дополнения. Выбирая, например, i -ю строку или
j -й столбец мы получим соответственно две формулы для вычисления определителя n -го порядка:
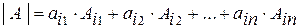 , (1.3)
, (1.3)
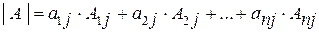 . (1.4)
. (1.4)
Задача 1.3. Вычислить определитель 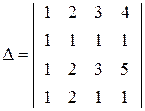 , раскладывая его по первой строке.
, раскладывая его по первой строке.
Решение. Воспользуемся формулой (1.3), выбрав для разложения определителя первую строку (i = 1):
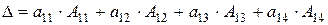 .
.
Таким образом,
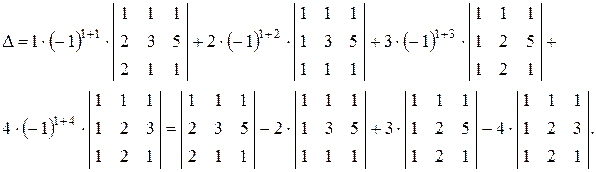
Вычисляя каждый из определителей третьего порядка по правилу треугольников, получим:
D = (3 + 2 + 10 – 6– 5 –2) – 2×(3 + 5 + 1 – 3 –1 – 5) + 3×(2 + 2 + 5 – 2 –10 – 1) –
– 4×(2 + 2 + 3 – 2 – 6 – 1) = 2 – 12 + 8 = – 2.
Перечислим без доказательства некоторые основные свойства определителя:
Свойство 1. При транспонировании величина определителя не меняется. Транспонированием называется такое преобразование матрицы, при котором строки меняются местами с соответствующими столбцами (первая строка становится первым столбцом, вторая строка – вторым столбцом, и т.д.). Другими словами транспонирование – это поворот матрицы вокруг ее главной диагонали. Таким образом:
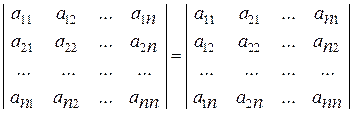 .
.
Из первого свойства следует, что все остальные свойства, сформулированные для строк определителя,– справедливы также и для его столбцов.
Свойство 2. Постоянный множитель из любой строки можно выносить за знак определителя:
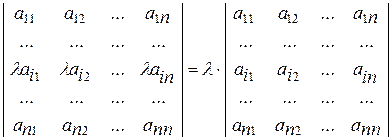 .
.
Свойство 3. Если определитель содержит две одинаковые строки, то он равен нулю.
Свойство 4. При перестановке двух строк местами определитель меняет знак на противоположный.
Свойство 5. Если определитель содержит несколько линейно зависимых строк, то определитель равен нулю. Строки 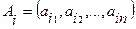 ,
, 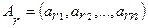 ,…,
,…, 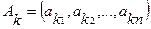 определителя называются линейно зависимыми, если существуют такие числа
определителя называются линейно зависимыми, если существуют такие числа 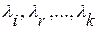 , не равные нулю одновременно, и такие, что
, не равные нулю одновременно, и такие, что 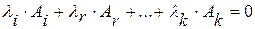 .
.
Выражение вида 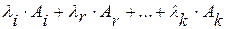 называется линейной комбинацией строк
называется линейной комбинацией строк 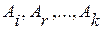 .
.
Свойство 6. Если к произвольной строке определителя прибавить линейную комбинацию других его строк, то величина определителя не изменится.
Задача 1.4. Вычислить определитель 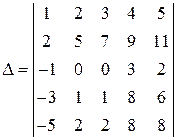 .
.
Решение. Используя свойства определителя, приведем матрицу определителя к треугольному виду. Выполним первую серию преобразований: 1) первую строку оставим без изменений; 2) из второй строки вычтем удвоенную первую строку, записав результат во второй строке; 3) к третьей строке прибавим первую строку; 4) вычтем из четвертой строки третью строку, умноженную на 3; 5) из пятой строки вычтем третью строку, умноженную на 5. Тогда получим:
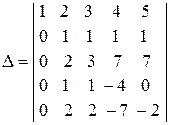 .
.
Произведем следующую серию преобразований: 1) первую и вторую строку оставим без изменений; 2) из третьей строки вычтем удвоенную вторую строку;
3) из четвертой строки вычтем вторую строку; 5) из пятой строки вычтем четвертую строку, умноженную на 2. Получим
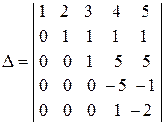 .
.
Поменяв четвертый и пятый столбец местами и внеся, после этого знак
(–) в четвертую строку, получим
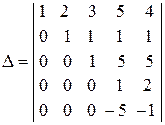 .
.
Наконец, прибавив к пятой строке четвертую строку, умноженную на 5 и затем, раскладывая определитель по первому столбцу, получим:
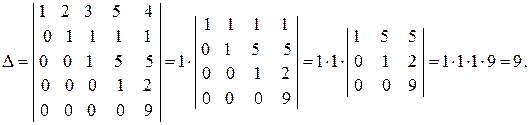
 2015-04-01
2015-04-01 1669
1669