Исходные данные для электрического расчета:
1) Диаметр (радиус) закаливаемого цилиндра: 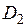 = 20·10–3 м (
= 20·10–3 м (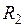 = 10·10–3 м).
= 10·10–3 м).
2) Глубина закаленного слоя: 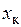 = 1,5·10–3 м.
= 1,5·10–3 м.
3)Частота тока индуктора: 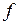 = 66 кГц.
= 66 кГц.
4) Длина закалочного индуктора: 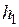 = 20·10–3 м.
= 20·10–3 м.
5) Удельное электрическое сопротивление: меди индуктора при 20 °С 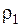 = 2·10–8 Ом·м и стали цилиндра (среднее в интервале температур 0…800 °С)
= 2·10–8 Ом·м и стали цилиндра (среднее в интервале температур 0…800 °С) 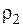 = 10–6 Ом·м.
= 10–6 Ом·м.
Требуется определить диаметр индуктора 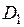 , толщину стенки трубки индуктора
, толщину стенки трубки индуктора 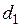 , напряжение на индукторе
, напряжение на индукторе 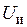 , ток индуктора
, ток индуктора 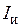 , коэффициент мощности индуктора
, коэффициент мощности индуктора 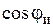 , коэффициент полезного действия индуктора
, коэффициент полезного действия индуктора 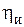 , мощность, подводимую к индуктору
, мощность, подводимую к индуктору 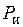 .
.
Обычно рассчитывают одновитковый индуктор и, если задано напряжение на индукторе, определяют число витков. В нашем случае будет использован одновитковый индуктор и напряжение на индукторе будет подбираться соотношением числа витков первичной и вторичной обмоток трансформатора.
Решение:
1) Внутренний диаметр индуктора:
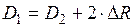 ,
,
где 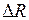 — зазор между индуктором и закаливаемой деталью. Обычно зазор
— зазор между индуктором и закаливаемой деталью. Обычно зазор 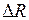 выбирается в пределах 2…5 мм при
выбирается в пределах 2…5 мм при 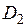 < 50 мм и 5…10 мм при
< 50 мм и 5…10 мм при 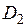 > 100 мм. Выбираем для закалки цилиндра
> 100 мм. Выбираем для закалки цилиндра 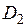 = 20·10–3 м зазор
= 20·10–3 м зазор 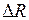 = 3·10–3 м.
= 3·10–3 м.
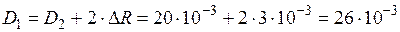 м.
м.
2) Глубина проникновения тока в материал индуктора (медь) определяется по формуле:
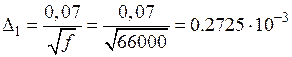 м,
м,
3) Толщина стенки медной трубки индуктора.
При одновременном нагреве, если индуктор не имеет постоянного охлаждения и охлаждается после окончания нагрева закалочной жидкостью, его токонесущая стенка выполняется достаточно массивной.
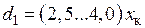 .
.
Обычно нижний предел выбирается при 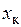 > 5·10–3 м. При непрерывно-последовательном нагреве, а также при одновременном нагреве, если индуктор имеет постоянное охлаждение, толщина трубки равна:
> 5·10–3 м. При непрерывно-последовательном нагреве, а также при одновременном нагреве, если индуктор имеет постоянное охлаждение, толщина трубки равна:
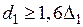 ,
,
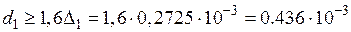 м.
м.
Принимаем толщину трубки индуктора 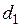 = 2·10–3 м.
= 2·10–3 м.
4) Расчетный диаметр детали.
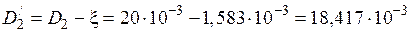 м.
м.
Расчетный диаметр детали 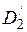 необходим для определения удельной мощности
необходим для определения удельной мощности 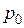 , которая рассчитывается для внешней поверхности детали. Так как мы используем в расчете формулы для плоской волны, разворачивая нагреваемый слой по расчетному диаметру, то и удельную мощность следует пересчитать на расчетную поверхность слоя, увеличив ее в
, которая рассчитывается для внешней поверхности детали. Так как мы используем в расчете формулы для плоской волны, разворачивая нагреваемый слой по расчетному диаметру, то и удельную мощность следует пересчитать на расчетную поверхность слоя, увеличив ее в 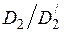 раз.
раз.
5) Приведенное значение удельной мощности:
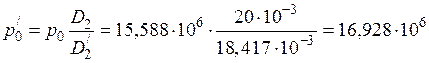 Вт/м2.
Вт/м2.
6) Относительная магнитная проницаемость на границе сред 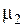 .
.
По рассчитанному значению 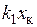 (
(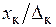 ) и задаваясь несколькими значениями
) и задаваясь несколькими значениями 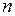 (а значит,
(а значит, 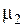 ), который учитывает изменение электрических параметров (
), который учитывает изменение электрических параметров (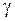 и
и 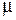 ) на границе двух сред, находим по табл. П.2–П.6 (см. Приложение) соответствующие значения коэффициентов, учитывающих влияние второй среды на электрическое сопротивление
) на границе двух сред, находим по табл. П.2–П.6 (см. Приложение) соответствующие значения коэффициентов, учитывающих влияние второй среды на электрическое сопротивление 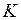 , соотношение напряженностей магнитного поля на поверхности и на границе сред
, соотношение напряженностей магнитного поля на поверхности и на границе сред 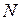 , а также
, а также 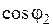 (и
(и 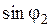 ), определяющие соотношение между внутренними активным и реактивным сопротивлениями цилиндра. Методика определения
), определяющие соотношение между внутренними активным и реактивным сопротивлениями цилиндра. Методика определения 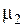 приведена в работах [1, 3].
приведена в работах [1, 3].
Расчет повторяем, пока полученные данные не позволят получить вариант, когда 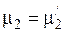 .
.
6.1) Выбираем 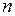 = –0,6, что соответствует
= –0,6, что соответствует 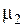 = 16 (см.). Для этого значения
= 16 (см.). Для этого значения 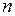 и
и 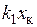 = 0,771 определяем по табл. П.2–П.5 (см. Приложение):
= 0,771 определяем по табл. П.2–П.5 (см. Приложение):
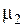 = 16,
= 16, 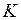 = 1,0075,
= 1,0075, 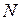 = 5.427,
= 5.427, 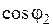 = 0,863.
= 0,863.
После этого определяем по формуле с учетом приведенного значения мощности 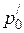 :
:
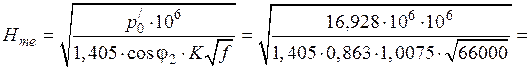
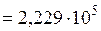 А/м.
А/м.
Определяем также напряженность магнитного поля на границе сред:
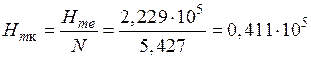 А/м.
А/м.
По табл. П.7 (см. Приложение) находим 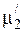 = 38,79. Результаты расчетов
= 38,79. Результаты расчетов 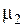 ,
, 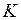 ,
, 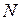 ,
, 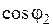 ,
, 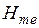 и
и 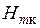 , а также
, а также 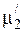 сведены в табл. 2.4. Поскольку
сведены в табл. 2.4. Поскольку 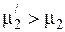 , расчет продолжаем.
, расчет продолжаем.
6.2) Выбираем 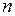 = –0,7 и
= –0,7 и 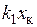 = 0,771.
= 0,771.
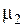 = 32,
= 32, 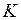 = 1,0086,
= 1,0086, 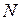 = 7,238,
= 7,238, 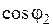 = 0,883.
= 0,883.
После этого определяем по формуле:
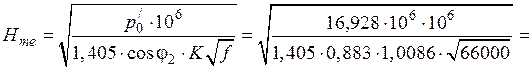
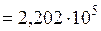 А/м.
А/м.
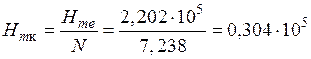 А/м.
А/м.
По табл. П.7 (см. Приложение) находим 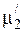 = 50,54.
= 50,54.
6.3) Выбираем 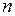 = –0,8 и
= –0,8 и 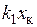 = 0,771.
= 0,771.
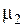 = 81,
= 81, 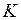 = 1,0098,
= 1,0098, 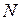 = 10,91,
= 10,91, 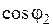 = 0.902.
= 0.902.
После этого определяем по формуле:
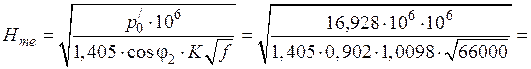
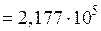 А/м.
А/м.
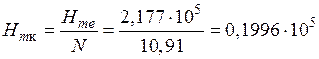 А/м.
А/м.
По табл. П.7 (см. Приложение) находим 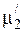 = 71,33.
= 71,33.
Результаты решения сводим в таблицу 2.4.
Таблица 2.4 Результаты расчетов по определению относительной магнитной проницаемости на границе сред 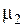 | |||||||
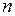 | 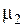 | 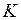 | 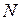 | 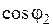 | 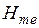 | 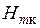 | 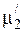 |
| –0,6 | 1,0075 | 5,427 | 0,863 | 2,229·105 | 0,411·105 | 38,79 | |
| –0,7 | 1,0086 | 7,238 | 0,883 | 2,202·105 | 0,304·105 | 50,54 | |
| –0,8 | 1,0098 | 10,91 | 0,902 | 2,177·105 | 0,1996·105 | 71,33 |
Построив графики 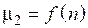 и
и 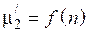 , изображенные на рис. 2.3, получим точку пересечения, где
, изображенные на рис. 2.3, получим точку пересечения, где 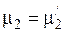 =72,65, которая соответствует
=72,65, которая соответствует 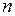 = –0,79.
= –0,79.
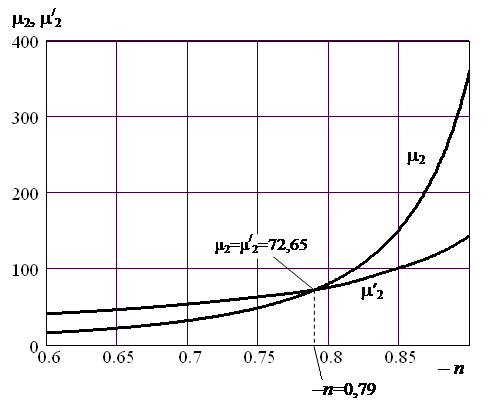
Рис. 2.3. Зависимости 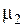 и
и 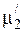 от параметра
от параметра 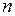
Для 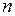 = –0,79 и
= –0,79 и 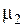 = 72,65 при
= 72,65 при 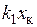 = 0,771 путем интерполяции данных табл. П.3–П.6 определяем параметры
= 0,771 путем интерполяции данных табл. П.3–П.6 определяем параметры 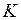 ,
, 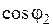 ,
, 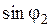 . Результаты расчета сведены в табл. 2.5.
. Результаты расчета сведены в табл. 2.5.
Таблица 2.5 Результаты расчета параметров 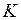 , , 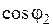 , , 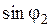 | |||
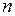 | 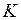 | 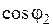 | 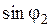 |
| –0,7 | 1,0086 | 0,883 | 0,469 |
| –0,79 | 1,0097 | 0,900 | 0,435 |
| –0,8 | 1,098 | 0,902 | 0,432 |
Таким образом, 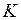 = 1,0097,
= 1,0097, 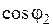 = 0,900,
= 0,900, 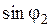 = 0,435.
= 0,435.
7) Активное и внутреннее реактивное сопротивление заготовки (решение проводится для горячего режима, когда в слое 0 ≤ 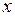 ≤
≤ 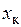 = 1,5 10–3 м —
= 1,5 10–3 м — 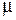 = 1, а на границе этого слоя при
= 1, а на границе этого слоя при 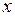 =
= 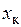 = 1,5 10–3 м —
= 1,5 10–3 м — 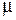 = 72,65, по формулам и):
= 72,65, по формулам и):
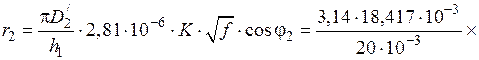
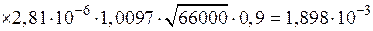 Ом,
Ом,
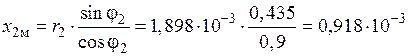 Ом.
Ом.
8) Реактивное сопротивление, учитывающее магнитное сопротивление замыкания магнитного потока вне индуктора (формула):
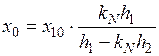 ,
,
где 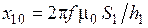 — реактивное сопротивление отрезка
— реактивное сопротивление отрезка 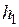 пустого индуктора,
пустого индуктора, 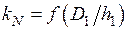 — коэффициент Нагаока, учитывающий краевые эффекты короткого индуктора (находится с помощью табл. П.8 Приложения в зависимости от
— коэффициент Нагаока, учитывающий краевые эффекты короткого индуктора (находится с помощью табл. П.8 Приложения в зависимости от 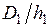 ).
).
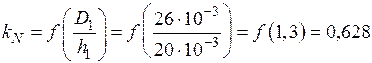 .
.
После этого определяем, учитывая, что 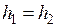 :
:
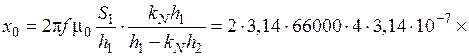
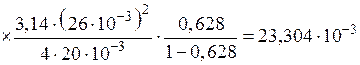 Ом.
Ом.
9) Реактивное сопротивление рассеяния, учитывающее магнитное сопротивление магнитному потоку, проходящему в зазоре между индуктором и деталью, определим по формуле:
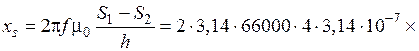
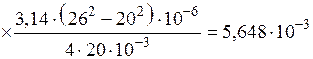 Ом.
Ом.
10) Коэффициент приведения активного и реактивного сопротивлений детали к току индуктора с учетом краевых эффектов системы индуктор–деталь определим по формуле:
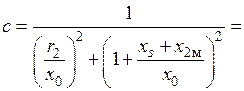
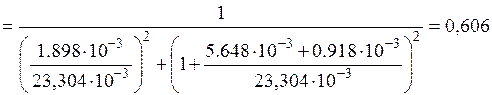 .
.
11) Приведенное активное сопротивление заготовки определяется по формуле:
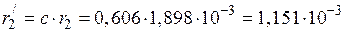 Ом.
Ом.
12) Приведенное реактивное сопротивление заготовки определяется по формуле:
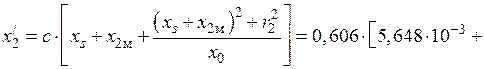
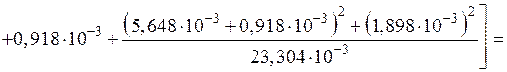
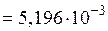 Ом.
Ом.
13) Активное и внутреннее реактивное сопротивление индуктирующего провода.
Поскольку поверхностный эффект в материал индуктора при толщине трубки 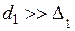 ярко выражен, активное и внутреннее реактивное сопротивление равны сопротивлению постоянному току полосы длиной
ярко выражен, активное и внутреннее реактивное сопротивление равны сопротивлению постоянному току полосы длиной 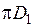 шириной
шириной 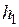 и толщиной
и толщиной 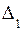 (см.):
(см.):
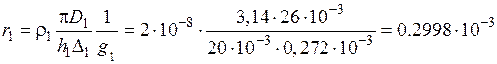 Ом,
Ом,
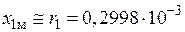 Ом.
Ом.
Здесь коэффициент 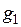 , учитывающий увеличение сопротивления индуктора из-за отверстий для подачи охлаждающей жидкости принят равным единице (
, учитывающий увеличение сопротивления индуктора из-за отверстий для подачи охлаждающей жидкости принят равным единице (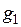 =1).
=1).
14) Эквивалентные активное, реактивное и полное сопротивления индуктора (см. схему замещения на рис. 1.9 и формулы и):
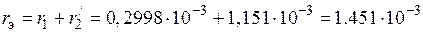 Ом,
Ом,
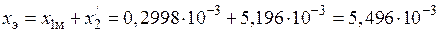 Ом,
Ом,
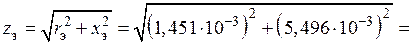
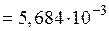 Ом.
Ом.
15) Ток индуктора в одновитковом индукторе:
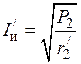 ,
,
где 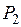 — мощность, передаваемая в нагреваемую деталь, она определена в п. 11 теплового расчета:
— мощность, передаваемая в нагреваемую деталь, она определена в п. 11 теплового расчета: 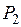 = 19588 Вт.
= 19588 Вт.
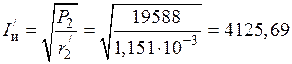 А.
А.
16) Напряжение на индуктирующем проводе одновиткового индуктора:
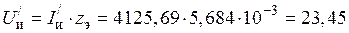 В.
В.
Принимаем число витков индуктора 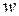 = 1.
= 1.
17) Плотность тока в индуктирующем проводе индуктора:
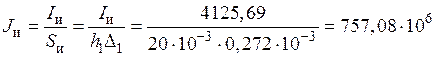 А/м2.
А/м2.
При непрерывной работе в индуктирующем проводе плотность тока 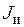 должна быть меньше (350…400)·106 А/м2. При индукционной поверхностной закалке режим — повторно-кратковременный, и предельная удельная мощность допускается 4·106 Вт/м2. В связи с этим необходимо проверить, допустима ли удельная мощность
должна быть меньше (350…400)·106 А/м2. При индукционной поверхностной закалке режим — повторно-кратковременный, и предельная удельная мощность допускается 4·106 Вт/м2. В связи с этим необходимо проверить, допустима ли удельная мощность 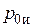 . Это будет сделано в п.20–21.
. Это будет сделано в п.20–21.
18) Мощность, выделяющаяся в индуктирующем проводе:
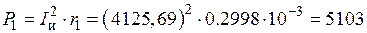 Вт.
Вт.
19) Удельная мощность, выделяющаяся в индукторе:
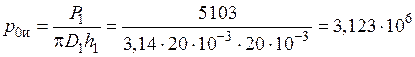 Вт/м2.
Вт/м2.
Эта мощность меньше предельной 4·106 Вт/м2 (см. стр. 59).
20) Активное сопротивление шин, т.е. двух полос, включенных последовательно, каждая из которых имеет длину 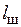 , ширину
, ширину 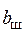 (среднюю) и толщину много больше
(среднюю) и толщину много больше 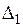 (см.рис. 2.1).
(см.рис. 2.1).
Длина каждой шины: 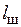 = 0,15 м.
= 0,15 м.
Ширина шин (средняя на участке от индуктора, где 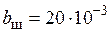 м, до трансформатора, где
м, до трансформатора, где 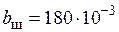 м):
м):
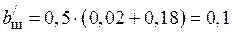 м.
м.
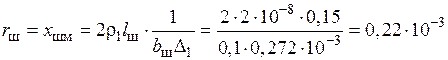 Ом.
Ом.
21) Индуктивное сопротивление шин с учетом индуктивного сопротивления, обусловленного магнитным потоком в зазоре:
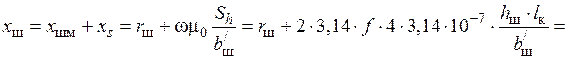
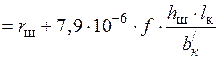 ,
,
где 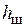 = 2·10–3 м — зазор между шинами.
= 2·10–3 м — зазор между шинами.
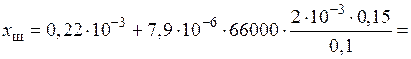
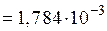 Ом.
Ом.
22) Активное, реактивное и полное сопротивления индуктора с токоподводящими шинами:
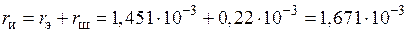 Ом,
Ом,
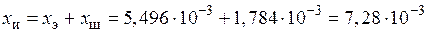 Ом,
Ом,
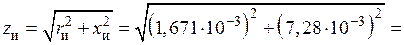
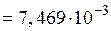 Ом.
Ом.
23) Коэффициент полезного действия индуктора:
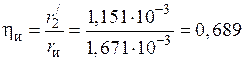 .
.
24) Коэффициент мощности индуктора:
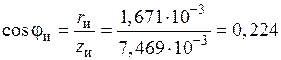 .
.
25) Мощность, подводимая к индуктору:
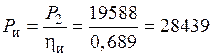 Вт.
Вт.
26) Напряжение на индукторе:
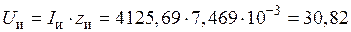 В.
В.
27) Реактивная мощность конденсаторной батареи:
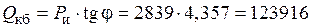 В·Ар.
В·Ар.
28) Емкость конденсаторной батареи
Индуктор, к которому необходимо подвести мощность 28,5 кВт при напряжении 31 В, должен быть подключен к источнику питания через высокочастотный нагрузочный трансформатор (см. рис. 2.4). Учитывая, что падение напряжения на вторичной обмотке трансформатора составляет ~10% от 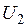 , определим коэффициент трансформации при напряжении транзисторного генератора 400 В (см. табл. 1.1):
, определим коэффициент трансформации при напряжении транзисторного генератора 400 В (см. табл. 1.1):
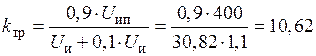 .
.
Принимаем 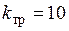 .
.
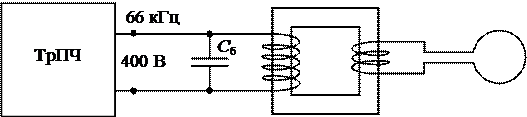
Рис. 2.4. Схема подключения индуктора к источнику питания
Реактивное сопротивление конденсаторной батареи, которая должна компенсировать индуктивное сопротивление трансформатора с подключенным на вторичной стороне индуктором (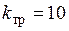 ):
):
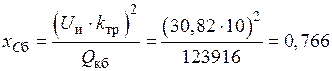 Ом.
Ом.
Емкость конденсаторной батареи:
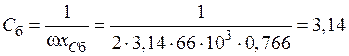 мкФ.
мкФ.
Для нормальной работы и возможного изменения параметров из-за принятых допущений при расчете и неточностях при изготовлении необходимо иметь запас ~20%.
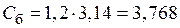 мкФ, т.е.
мкФ, т.е. 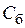 =3,5…4 мкФ.
=3,5…4 мкФ.
Необходимо также иметь в виду, что напряжение на конденсаторной батарее 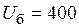 В. Поэтому реактивная мощность конденсаторной батареи будет равна:
В. Поэтому реактивная мощность конденсаторной батареи будет равна:
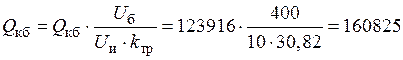 В·Ар.
В·Ар.
Результаты теплового и электрического расчетов варианта №2 приведены в табл. П.10.
 2015-04-01
2015-04-01 6028
6028
