Цель: формирование умения классифицировать числовые последовательности и вычислять их пределы.
Задание для самостоятельной внеаудиторной работы: 
& 11.1.Выучите определение числовой последовательности, видов числовой последовательности (возрастающей, убывающей, ограниченной), предела числовой последовательности.
?11.2. Выпишите первые пять членов числовой последовательности, классифицируйте данную последовательность по критериям монотонности и ограниченности, найдите её предел:
а) аn = 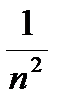 ; б) аn =
; б) аn = 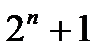 ; в) аn =
; в) аn = 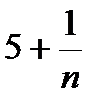 ; ¶г) аn =
; ¶г) аn = 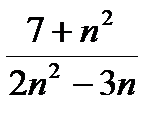 .
.
?11.3. Используя материал учебника, составьте конспект по теме «Бесконечно малые и бесконечно большие числовые последовательности, число е» по следующему плану:
- определение бесконечно малой числовой последовательности, пример такой последовательности;
- определение бесконечно большой числовой последовательности, пример такой последовательности;
- теорема, устанавливающая связь между бесконечно малыми и бесконечно большими числовыми последовательностями;
- теорема Вейерштрасса (признак существования предела последовательности);
- числовая последовательность, приводящая к числу е.
?11.4. Найдите предел числовой последовательности:
а) 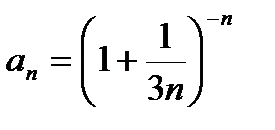 ; б)
; б) 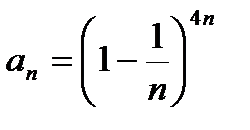 ; ¶в)
; ¶в) 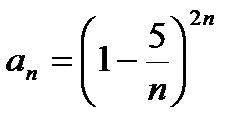 ; ¶г)
; ¶г) 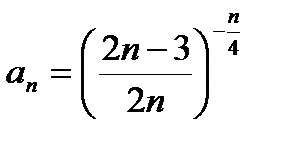 .
.
i11.5. Используя дополнительную литературу, найдите апории философа Зенона Эллийского (490-430 г. до н.э.) - задачи, содержащие в себе противоречия. Попробуйте объяснить причину возникающих противоречий с точки зрения математики. Возможно ли решение этих задач на основании понятия предела последовательности?
Методические указания по выполнению работы:
Знание следующего теоретического материала будет Вам полезно при классификации и нахождении предела числовой последовательности.
Бесконечной числовой последовательностью называется функция 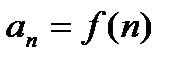 , заданная на множестве натуральных чисел (п
, заданная на множестве натуральных чисел (п 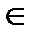 N). Для обозначения числовой последовательности принята следующая запись: { аn }.
N). Для обозначения числовой последовательности принята следующая запись: { аn }.
Последовательность { аn } называется убывающей, если каждый последующий член последовательности меньше или равен предыдущему, т.е. если 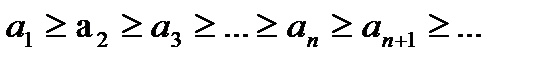 (
(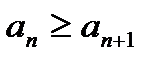 ) для всех п
) для всех п 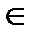 N.
N.
Последовательность { аn } называется возрастающей, если каждый последующий член последовательности больше или равен предыдущему (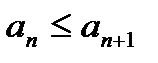 ).
).
Последовательность { аn } называется ограниченной, если существуют числа М и m такие, что для любого номера n имеет место неравенство: m £ a n £ M.
Геометрически ограниченность последовательности { аn } означает существование отрезка [ m; M ], на котором помещены все члены этой последовательности. Для неограниченной последовательности { аn } отрезка [ m; M ], которому принадлежат все члены an, не существуют.
Число a называется пределом последовательности { аn }, если для любого наперед заданного положительного числа e найдется такое натуральное число N, что для любого номера элемента
n > N выполняется неравенство: | an – a | < e. В этом случае пишут 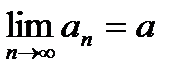 .
.
Последовательность, имеющая конечный предел, называется сходящейся, а не имеющая предела – расходящейся.
Для практического нахождения пределов числовых последовательностей используют следующие свойства пределов:
Пусть { аn } и { bn } – сходящиеся последовательности, т.е. 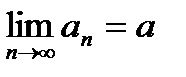 ,
, 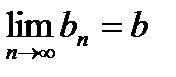 . Тогда справедливы следующие утверждения:
. Тогда справедливы следующие утверждения:
1. Всякая сходящаяся последовательность имеет только один предел.
2. Для любого числа k последовательность { kаn } также сходится, причем 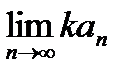 =
= 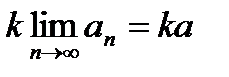 .
.
3. Сумма (разность) аn± bn также сходится, причем
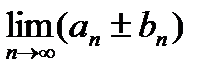 =
= 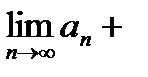
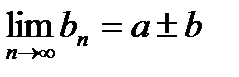 .
.
4. Произведение аn bn также сходится, причем
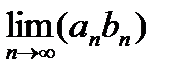 =
= 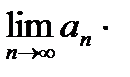
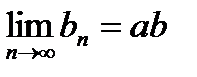 .
.
5. При дополнительном условии b≠0 частное 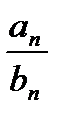 также сходится, причем
также сходится, причем 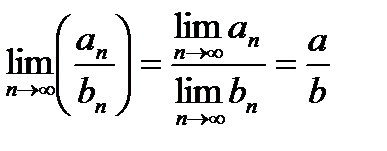 .
.
Проиллюстрируем использование теоретического материала при исследовании числовых последовательностей.
Пример 1. Исследуйте числовую последовательность аn = 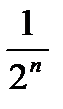 .
.
Решение: Выпишем элементы числовой последовательности, поочерёдно подставляя вместо n значения 1, 2, 3, 4, 5 и т.д. Получим бесконечное числовое множество: { 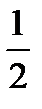 ;
; 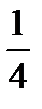 ;
; 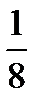 ;
; 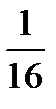 ;
; 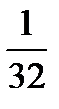 ; …}
; …}
Последовательности 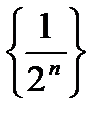 соответствует следующее геометрическое изображение:
соответствует следующее геометрическое изображение:
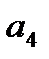
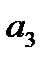
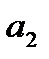
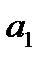
а
0 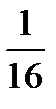
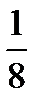
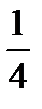
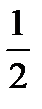 1
1
Последовательность 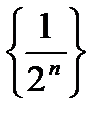 убывающая, т.к.
убывающая, т.к. 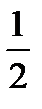 >
> 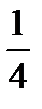 >
> 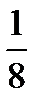 >
> 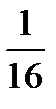 > … >
> … > 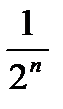 > …
> …
Она ограничена, т.к. существует m =0 и М = 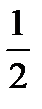 , такие, что 0£ an £
, такие, что 0£ an £ 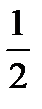 . Геометрически все элементы последовательности
. Геометрически все элементы последовательности 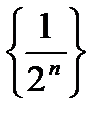 принадлежат промежутку (0;
принадлежат промежутку (0; 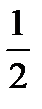 ].
].
Покажем, что 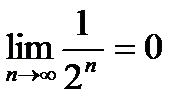 . Выберем любую точность e >0(например, e= 0,001). Тогда найдется натуральное число N (в нашем случае N =9), такое что для всех n > N выполняется неравенство:
. Выберем любую точность e >0(например, e= 0,001). Тогда найдется натуральное число N (в нашем случае N =9), такое что для всех n > N выполняется неравенство: 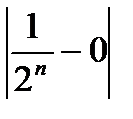 < e (уже для п =10
< e (уже для п =10 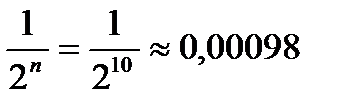 будет меньше e= 0,001).
будет меньше e= 0,001).
Пример 2. Исследуйте числовую последовательность 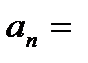 3 п -2.
3 п -2.
Решение: Подставляя вместо n значения 1, 2, 3 и т.д., найдем следующие элементы последовательности: {1; 4; 7; 10; 13; 16…}.
Последовательности {3 п -2} соответствует следующее изображение:
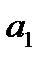
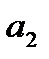
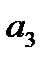
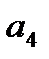
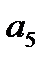
а

Последовательность {3 п -2} является возрастающей, т.к. каждый следующий член последовательности больше предыдущего: 1 < 4 < 7 < 10 < … < 3 п -2< …
Она не ограничена, т.к. не существует числа М, которое бы ограничивало последовательность сверху.
Последовательность {3 п -2} не имеет предела, т.к. ее элементы неограниченно возрастают, следовательно, эта последовательность является расходящейся (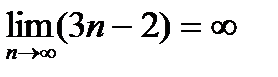 ).
).
Пример 3. Найдите предел последовательности 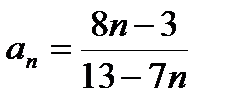 .
.
Решение. Числитель и знаменатель представляют собой расходящиеся последовательности (так как они не ограничены), поэтому непосредственно применять теорему о пределе частного нельзя. В этом случае поступим так: числитель и знаменатель разделим на п (от этого дробь не изменится), а затем применим теоремы о пределах последовательностей. Приведем подробную запись вычисления предела:
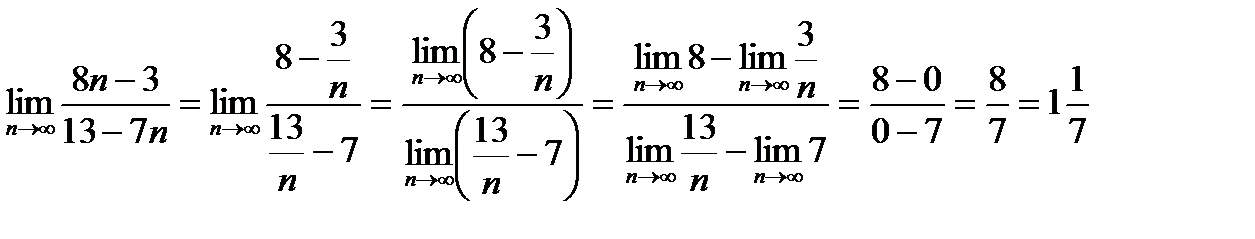 .
.
Ответ: 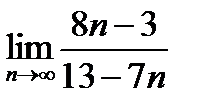 =
= 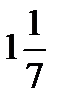
При составлении конспекта по теме «Бесконечно малые и бесконечно большие числовые последовательности, число е» воспользуйтесь памяткой 6.
Список литературы:
1. Григорьев В.П. Элементы высшей математики: Учеб. для студ. учреждений СПО / В.П.Григорьев, Ю.А.Дубинский - М.: Издательский центр "Академия", 2012. – 320с. – Глава 4, §4.1-4.4, стр. 82 – 95.
2. Источники литературы, найденные самостоятельно.
3. Материалы сети Интернет.
 2015-04-01
2015-04-01 1232
1232