2015-04-01
1263
Часто в практических вычислениях нужны не все собственные значения, а лишь некоторые из них.
Для решения частичной проблемы собственных значений, состоящей в определении одного или нескольких собственных значений и соответствующих им собственных векторов, обычно используют итерационные методы. Строится такой итерационный процесс, который сходится к одному собственному значению и собственному вектору, причем используемые алгоритмы весьма экономичны.
Построим итерационный процесс, применяя метод итераций к решению систем уравнений
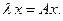(11)
Представим (11) через вспомогательный вектор у:
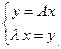(12)
Пусть х (0)–начальное приближение собственного вектора х, причем собственные векторы на каждой итерации нормированы, так что
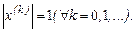
Используя соотношение (12), получим:
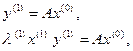
или, применяя умножение обеих частей равенства скалярно на х (0), получим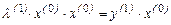 
, учитывая, что 
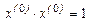, запишем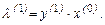 
Следующие приближения можно вычислить, нормируя у(1). Окончательно итерационный процесс записывается в виде:
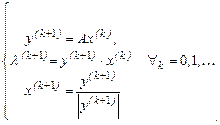(13)
Процесс (13) продолжается до установления постоянных значений λ и х. При этом нужно учесть, что, применяя критерии завершения итераций, следует проверять близость векторов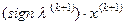 
и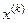 
.
|
|
|
Можно показать, что найденное значение λ является наибольшим по модулю собственным значением данной матрицы А, а х – соответствующим ему вектором.
Скорость сходимости этого итерационного процесса зависит от удачного выбора начального приближения.
Для решения системы (11) можно использовать и другие итерационные методы.
В некоторых задач нужно искать не наибольшие, а наименьшие по модулю собственные значения матрицы А. В этом случае можно умножить (11) на матрицу А -1
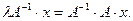(14)
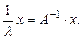(15)
Следовательно, 1/ l является собственным значением обратной матрицы, и задача (15) отличается от ранее рассмотренной тем, что здесь будет вычисляться наибольшее по модулю собственное значение1/ l матрицы А –1, что будет достигнуто при наименьшем по модулю λ.
