Понятие квадратичной формы

Квадратичной формой 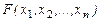от n неизвестных 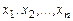называется сумма, каждое слагаемое которой является квадратом одного из этих неизвестных или произведением двух разных неизвестных

Пример. 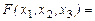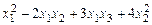является квадратичной формой от трех неизвестных 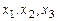. Каждую квадратичную форму можно записать в стандартном виде. Для этого сначала приведем подобные в квадратичной форме, затем обозначим коэффициент при 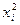через 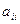, а коэффициент при произведении 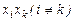через 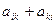, причем 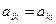. Член 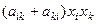запишем в виде 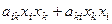. Теперь квадратичную форму можно записать в виде:

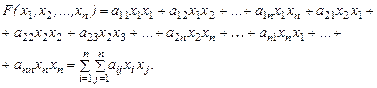
Матрица 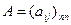называется матрицей квадратичной формы 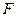. Так как 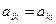, то – симметричная матрица.

Пример. Запишем предложенную (рассмотренную выше) квадратичную форму в стандартном виде и найдем матрицу.

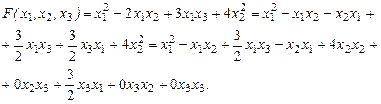
Матрица квадратичной формы имеет вид:

.

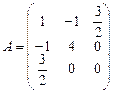Квадратичная форма может быть представлена в векторно-матричном виде

, .

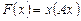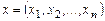Действительно: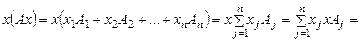

=

,

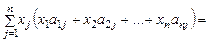
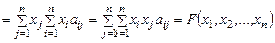здесь 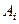– это i –й столбец матрицы .

Приведенные выкладки показывают в частности, что если А – симметричная матрица, то выражение 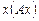является квадратичной формой от неизвестных .

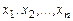Если a – произвольный 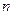-мерный вектор, то, подставляя в квадратичную форму a вместо x, получим число 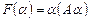, которое называют значением квадратичной формы 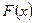на вектор a.