1.1 Для сферической и цилиндрической систем координат найти уравнения координатных поверхностей и координатных линий.
1.2 Записать квадрат расстояния между двумя бесконечно близкими точками в сферической системе координат. (Для сферической системы координат 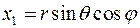 ,
, 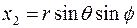 ,
, 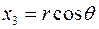 ).
).
Решение задачи 1.2 Искомая величина равна сумме квадратов полных дифференциалов декартовых координат 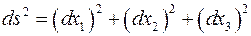 . Для их вычисления используем формулу
. Для их вычисления используем формулу 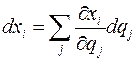 .
. 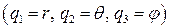
В результате получим 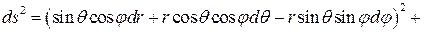
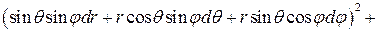
 . Раскроем скобки и упростим выражение. Итого:
. Раскроем скобки и упростим выражение. Итого: 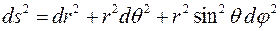
1.3 Записать квадрат расстояния между двумя бесконечно близкими точками в цилиндрической системе координат. (Для цилиндрической системы координат 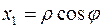 ,
, 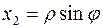 ,
, 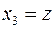 ).
).
Решение задачи 1.3 Вычислим сумму квадратов полных дифференциалов декартовых координат: 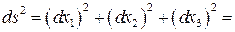
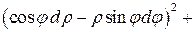
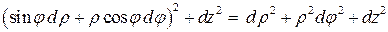
1.4 Найти коэффициенты Ламе для сферической и цилиндрической систем координат.
Решение задачи 1.4 Искомые значения коэффициентов Ламе легко найти, используя их определение 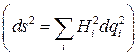 и ответы к задачам 1.2 и 1.3.
и ответы к задачам 1.2 и 1.3.
Для сферической системы координат:
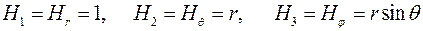 .
.
Для цилиндрической системы координат:
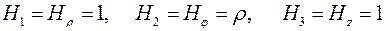 .
.
1.5 Записать формулы для длин ребер, площадей граней и объема бесконечно малого параллелепипеда, ограниченного координатными плоскостями, в сферической и цилиндрической системах координат.
1.6 Получить формулы для градиента скалярного поля 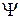 в сферической и цилиндрической системах координат.
в сферической и цилиндрической системах координат.
Решение задачи 1.6 для сферической системы координат. Подставим в выражение (1.1) найденные выше коэффициенты Ламе. Получим:
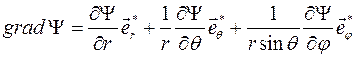
1.7 Получить формулы для дивергенции векторного поля 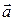 в сферической и цилиндрической системах координат.
в сферической и цилиндрической системах координат.
Решение задачи 1.7 для сферической системы координат. Подставим в выражение (1.2) найденные выше коэффициенты Ламе. Получим:
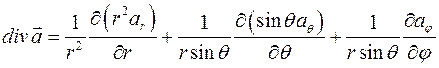
1.8 Получить формулы для ротора векторного поля 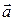 в сферической и цилиндрической системах координат.
в сферической и цилиндрической системах координат.
1.9 Получить формулы для лапласиана скалярного поля 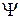 в сферической и цилиндрической системах координат.
в сферической и цилиндрической системах координат.
Решение задачи 1.9 Подставим в выражение (1.4) соответствующие коэффициенты Ламе. В итоге получим для сферической системы координат:
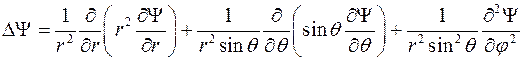
Соответственно для цилиндрической системы координат:
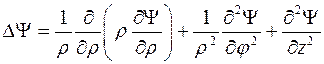
1.10 Найти 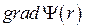 ,
, 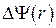 в сферической системе координат для функций:
в сферической системе координат для функций:
а) 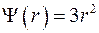 , б)
, б) 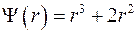 , в)
, в) 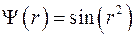
1.11 Найти 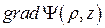 ,
, 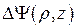 ,
, 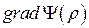 ,
, 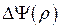 в цилиндрической системе координат для функций:
в цилиндрической системе координат для функций:
а) 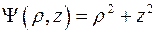 , б)
, б) 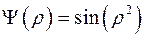 .
.
 2015-04-01
2015-04-01 1257
1257
