Криволинейные системы координат

Министерство образования и науки Российской Федерации

Федеральное агентство по образованию

Государственное образовательное учреждение

Высшего профессионального образования

«ЮЖНЫЙ ФЕДЕРАЛЬНЫЙ УНИВЕРСИТЕТ»

А.А. НОВАКОВИЧ

УЧЕБНО-МЕТОДИЧЕСКОЕ ПОСОБИЕ

ОСНОВЫ ВЕКТОРНОГО И ТЕНЗОРНОГО АНАЛИЗА

Часть II

для студентов бакалавриата

Ростов-на-Дону

Учебно-методическое пособие разработано кандидатом физико-математических наук, доцентом кафедры теоретической и вычислительной физики ЮФУ А.А. Новаковичем.

Ответственный редактор доктор физико-математических наук,

профессор Л. А. Бугаев.

Компьютерный набор и верстка А.А. Новакович.

Печатается в соответствии с решением кафедры теоретической и

вычислительной физики физического факультета ЮФУ,

протокол № 12 от 27 ноября 2007 г.

СОДЕРЖАНИЕ:

1. Криволинейные системы координат.………………………………… стр. 4

2. Векторы и тензоры. Их преобразования при поворотах

системы координат ………………………………………...………….. стр. 9

3. Действия над тензорами ……………………………………………… стр. 18

4. Свойства тензоров второго ранга ……….……………………………. стр. 25

5. Символ Леви-Чивита ………………………….……………………… стр. 33

6. Преобразование тензорных величин при инверсии ………..……….. стр. 37

7. Элементы тензорного анализа …………….…………………………. стр. 42

Литература……………………………………………………………… стр. 47

КРИВОЛИНЕЙНЫЕ СИСТЕМЫ КООРДИНАТ.

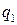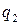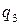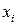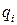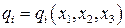Нередко удобно определять положение точки в пространстве не декартовыми координатами, а тремя другими величинами , , , более соответствующими характеру решаемой задачи. Эти величины называют криволинейными координатами. Если наложить должные ограничения на область изменения криволинейных координат, то можно добиться взаимно однозначного соответствия между переменными и : или 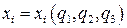, 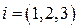. Поверхности, описываемые уравнением 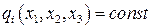, называются координатными. Линии пересечения двух координатных поверхностей называются координатными линиями. Понятно, что вдоль координатной линии изменяется только одна из трех криволинейных координат. Если координатные линии в каждой точке пространства взаимно перпендикулярны, криволинейные координаты называются ортогональными. Примерами ортогональных криволинейных координат являются сферическая система координат 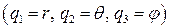и цилиндрическая система координат .

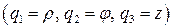Введем в каждой точке пространства орты 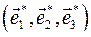, направленные по касательным к координатным линиям в сторону возрастания соответствующих переменных 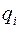. В ортогональных координатах эти орты взаимно перпендикулярны: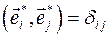

Определим частную производную радиус-вектора 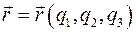по координате 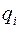. Приращение вектора 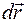при малом изменении переменной 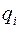направлено вдоль орта : ,

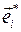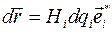так что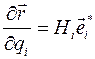

Положительные величины 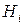называются коэффициентами Ламе.

Учтя, что 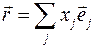, получим: 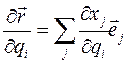. Отсюда .

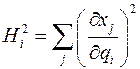Квадрат расстояния 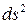между двумя бесконечно близкими точками выражается через квадраты коэффициентов Ламе по формуле:

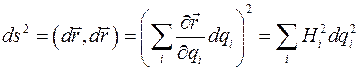
Если провести через две бесконечно близкие точки координатные поверхности, то они ограничат бесконечно малый прямоугольный параллелепипед с длинами ребер 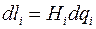. Грани этого параллелепипеда имеют площади: , , ,

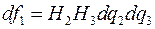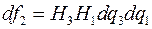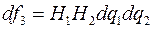а объем выражается формулой: .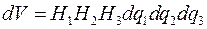

В ортогональной криволинейной системе координат выражение для градиента скалярного поля 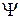имеет следующий вид:

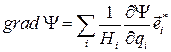(1.1)

Дивергенция векторного поля 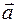в ортогональной криволинейной системе координат определяется по формуле:

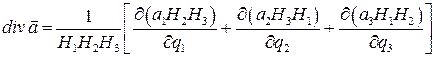(1.2)

Ротор векторного поля 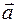в ортогональной криволинейной системе координат можно записать через определитель:

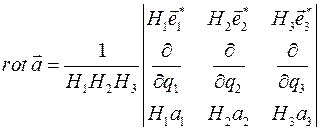(1.3)

Результат действия оператора Лапласа наскалярное поле определяется, как 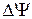=div grad 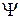. Из приведенных выше формул для градиента и дивергенции непосредственно следует его выражение в криволинейной ортогональной системе координат.

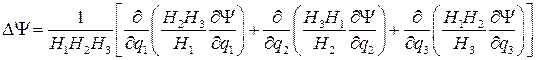. (1.4)