Определитель четвертого порядка есть число, которое находится следующим образом:
Δ 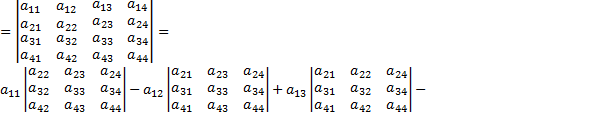
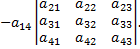
Определители третьего порядка в правой части равенства являются минорами элементов
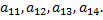
Алгебраическое дополнение элемента 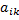 вычисляется по формуле
вычисляется по формуле 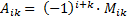 , тогда равенство можно переписать в виде: |А| =
, тогда равенство можно переписать в виде: |А| = 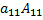 +
+ 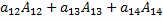 .
.
Эта формула дает разложение определителя четвертого порядка по элементам первой строки. Аналогично вычисляются определители более высоких порядков.
Все свойства Определителей второго и третьего порядка остаются справедливыми для определителей любого порядка.
Пример 1. Вычислить определители:
а) 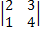 = 2·4-3·1=5.
= 2·4-3·1=5.
Ответ: 5.
б)  =
= 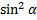 +
+ 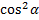 = 1.
= 1.
Ответ: 1.
в) 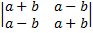 =
= 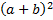 -
- 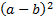 =
= 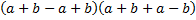 = 2
= 2 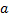 ·2
·2 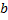 = 4
= 4 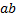 .
.
Ответ: 4 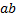 .
.
г) 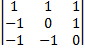 = 1·
= 1· 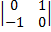 -1·
-1· 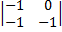 +1·
+1· 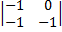 = 1-1+1= 1.
= 1-1+1= 1.
Второй способ. Воспользуемся свойством определителя и к первой строке прибавим третью, получим определитель третьего порядка и разложение по элементам первой строки:
в) 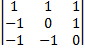 =
= 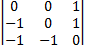 = 1 ·
= 1 · 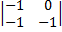 = 1.
= 1.
Ответ: 1.
 2015-04-01
2015-04-01 1057
1057








