Пусть в пространстве зафиксирована некоторая точка О(начало) и выбран векторный базис
 ,
,  ,
, 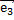 .
.
Определение 12. Совокупность {0;  ;
;  ;
; 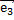 }называют декартовой системой координат в пространстве.
}называют декартовой системой координат в пространстве.
Определение 13. Три прямые проходящие через О и параллельные соответственно векторам  ,
,  ,
, 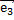 , называют осями координат и обозначают соответственно Оz,Oy,Oz.Мы будем всегда изображать векторы
, называют осями координат и обозначают соответственно Оz,Oy,Oz.Мы будем всегда изображать векторы  ,
,  ,
, 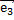 лежащими на соответственных осях.
лежащими на соответственных осях.
Определение 14. Координатами точки М в пространстве относительно декартовой системы координат {0;  ;
;  ;
; 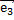 } называют координаты ее радиус-вектора
} называют координаты ее радиус-вектора 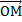 в этой системе.
в этой системе.
Иначе говоря, координаты точки М – это такие три числа х,у,zсоответственно абсцисса и ордината точки М; третью координату zназывают аппликатой точки М.
Введение в пространстве декартовой системы координат позволяет установить взаимно-однозначное соответствие между точками М пространства и упорядоченными тройками чисел x,y,z.
Определение 15. Координатами вектора 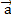 в пространстве относительно декартовой системы координат {0;
в пространстве относительно декартовой системы координат {0;  ;
;  ;
; 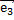 }называют координаты этого вектора в базисе
}называют координаты этого вектора в базисе  ;
;  ;
; 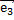 .
.
 2015-04-01
2015-04-01 604
604








