Определение 16. Векторы 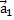 ,
,  называют линейно зависимыми, если существуют числа
называют линейно зависимыми, если существуют числа 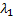 ,
, 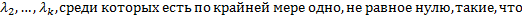
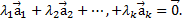 (***)
(***)
Это определение линейной зависимости векторов 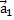 ,
,  эквивалентно такому: векторы
эквивалентно такому: векторы 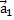 ,
,  линейно зависимы, если один из них можно представить в виде линейной комбинации остальных (или разложить по остальным).
линейно зависимы, если один из них можно представить в виде линейной комбинации остальных (или разложить по остальным).
Векторы 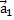 ,
,  называются линейно зависимыми, если равенство (***) возможно в единственном случае, когда
называются линейно зависимыми, если равенство (***) возможно в единственном случае, когда 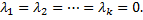
Понятие линейной зависимости играет большую роль в линейной алгебре. В векторной алгебре линейная зависимость имеет простой геометрический смысл.
1) Любые два коллинеарных вектора линейно зависимы, и наоборот, два неколлинеарных вектора линейно независимы.
2) Три компланарных вектора линейно зависимы, и наоборот, три некомпланарных вектора линейно независимы.
3) Каждые четыре вектора линейно зависимы.
Определение 17. Три линейно независимых вектора 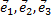 называются базисом пространства, т.е. любой вектор
называются базисом пространства, т.е. любой вектор  может быть представлен в виде некоторой
может быть представлен в виде некоторой 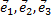 .
.
Определение 18. Два лежащих в плоскости линейно независимых вектора 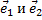 называют базисом плоскости, т.е. любой лежащий в этой плоскости вектор
называют базисом плоскости, т.е. любой лежащий в этой плоскости вектор  может быть представлен в виде линейной комбинации векторов
может быть представлен в виде линейной комбинации векторов 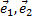 .
.
 2015-04-01
2015-04-01 587
587








