Задания для самостоятельного решения

1. Даны три вектора 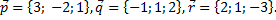Найти разложение вектора 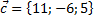по базису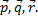

2. Даны векторы 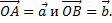Вектор 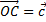–медиана треугольника OAB. Разложить вектор 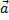по базису

3. В тетраэдре OABC точки K, L, M, N, P, Q – середины рёбер OA, OB, OC, AB, AC, BC соответственно, S – точка пересечения медиан треугольника ABC. Принимая за базисные

векторы 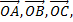найти в этом базисе координаты:

1) векторов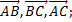

2) векторов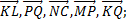

3) векторов 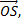и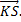

4. Точки Mи N – середины сторон BCи CDпараллелограмма ABCD. Разложить вектор 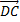по векторам 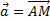и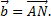

5. Дан куб ABCDEFGH. Разложить вектор 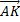, где K– центр грани DHGC, по векторам ,

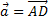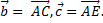
6. На плоскости даны вектора 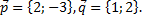Найти разложение вектора 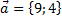по базису ,

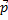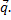
7. На плоскости даны три вектора 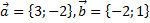и 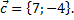Определить разложение каждого из этих трёх векторов, принимая в качестве базиса два других.

8. Принимая в качестве базиса векторы 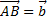и 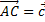, совпадающие со сторонами треугольника ABC, определить разложение векторов, приложенных в вершинах треугольника и совпадающих с его медианами.

9. Даны четыре вектора 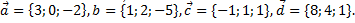Найти координаты векторов – линейных комбинаций: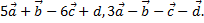

10. Даны четыре вектора 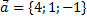, 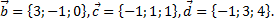Найти числа α, β, γ такие, что α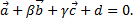

11. Проверить, что векторы 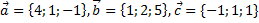образуют базис в пространстве. Найти координаты векторов 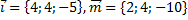, 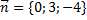в этом базисе.

12. (Задача об отрезке, разделённом в заданном отношении.) Пусть точка C, лежащая на отрезкеAB, делит этот отрезок в отношении λ, т.е. 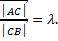Выразить вектор 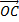через векторы 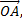и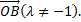

13. Даны две точки A(1;2;3). B(7;2;5). На прямой ABнайти такую точку M, чтобы точки Bи Mбыли расположены по разные стороны от точки A и чтобы отрезок AMбыл вдове длиннее отрезка AB. Система координат аффинная.

14. Вершина Aпараллелепипеда ABCD 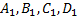принята за начало координат, а векторы 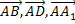– за базисные векторы. Найти в этой системе координаты всех вершин параллелепипеда.

15. Вершина Oтетраэдра OABCDпринята за начало координат, а векторы 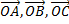– за базисные векторы. Найти на этой (аффинной) системе координаты точек пересечения медиан граней тэтраэдра.