Среди декартовых систем координат простейшей является прямоугольная декартова система координат.
Определение 1. Декартова система координат 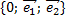 на плоскости называется прямоугольной, если
на плоскости называется прямоугольной, если 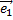 и
и 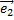 – ортогональные единичные векторы.
– ортогональные единичные векторы.
Аналогично определяется прямоугольная декартова система координат 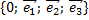 в пространстве; в этом случае векторы
в пространстве; в этом случае векторы 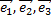 также являются взаимно перпендикулярными и единичными. Базисные векторы
также являются взаимно перпендикулярными и единичными. Базисные векторы 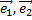 прямоугольной декартовой системы координат на плоскости обозначают обычно
прямоугольной декартовой системы координат на плоскости обозначают обычно 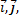 базисные векторы
базисные векторы 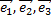 прямоугольной декартовой системы координат обозначают
прямоугольной декартовой системы координат обозначают 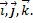 Соответственно разложение радиус-вектора
Соответственно разложение радиус-вектора 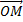 по базису записывают в виде
по базису записывают в виде
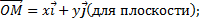
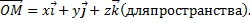
Определение 2. Проекцией вектора 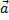 на единичный вектор
на единичный вектор 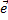 называется число
называется число 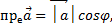 где
где 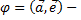 угол между векторами
угол между векторами 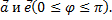
Координаты 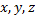 вектора
вектора 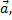 полученные как коэффициенты линейной комбинации базисных векторов, в прямоугольном базисе совпадают с проекцией вектора
полученные как коэффициенты линейной комбинации базисных векторов, в прямоугольном базисе совпадают с проекцией вектора 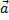 на базисные орты
на базисные орты 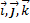 соответственно, а длина вектора
соответственно, а длина вектора 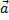 равна
равна 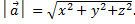
Определение 3. Числа 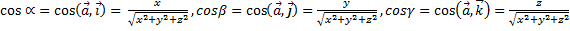 называется направляющими косинусами вектора
называется направляющими косинусами вектора 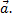
Направляющие косинусы вектора совпадают с координатами (проекциями) его орта 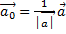 и между собой связаны соотношением
и между собой связаны соотношением 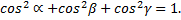
Отметим, что базис 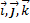 называют ортонормированным, так как
называют ортонормированным, так как 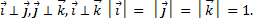
Пример 1. Заданы векторы 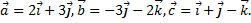 Найти:
Найти:
а) координаты вектора 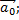
б) координаты вектора 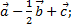
в) разложение вектора 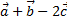 по базису
по базису 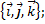
г) 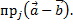
Решение.
а) Так как 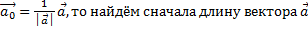 по формуле│
по формуле│ 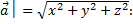
│ 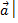 =
= 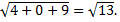 Тогда
Тогда 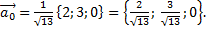
б) Вычислим координаты вектора 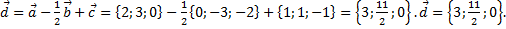
в) 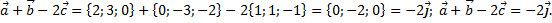
г) 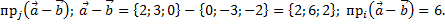
Ответ: 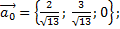
б) 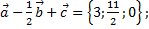
в) 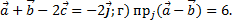
Замечание. Если известны координаты точек 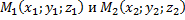 , то проекции X, Y, Z на оси координат вектора
, то проекции X, Y, Z на оси координат вектора 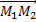 могут быть получены по формулам
могут быть получены по формулам 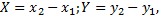
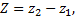 то расстояние d между данными точками определяется формулой:
то расстояние d между данными точками определяется формулой:
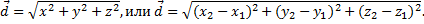
Если точка 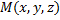 лежит на прямой, проходящей через две данные точки
лежит на прямой, проходящей через две данные точки 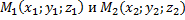 и дано отношение
и дано отношение 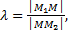 в котором точка M делит отрезок
в котором точка M делит отрезок 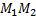 , то координаты точки M определяются по формулам:
, то координаты точки M определяются по формулам:
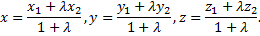
 2015-04-01
2015-04-01 795
795








