Это одно из преобразований Фурье, широко применяемых в алгоритмах цифровой обработки сигналов (его модификации применяются в сжатии звука в MP3, сжатии изображений в JPEG и др.), а также в других областях, связанных с анализом частот в дискретном (к примеру, оцифрованном аналоговом) сигнале. Дискретное преобразование Фурье требует в качестве входа дискретную функцию. Такие функции часто создаются путём дискретизации (выборки значений из непрерывных функций). Дискретные преобразования Фурье помогают решать частные дифференциальные уравнения и выполнять такие операции, как свёртки. Дискретные преобразования Фурье также активно используются в статистике, при анализе временных рядов. Преобразования бывают одномерные, двумерные и даже трёхмерные.
Прямое преобразование:
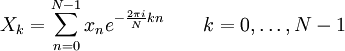
Обратное преобразование:
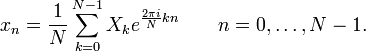
Обозначения:
§ N — количество значений сигнала, измеренных за период, а также количество компонент разложения;
§ 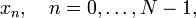 — измеренные значения сигнала (в дискретных временных точках с номерами
— измеренные значения сигнала (в дискретных временных точках с номерами 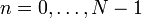 , которые являются входными данными для прямого преобразования и выходными для обратного;
, которые являются входными данными для прямого преобразования и выходными для обратного;
§ 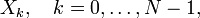 — N комплексных амплитуд синусоидальных сигналов, слагающих исходный сигнал; являются выходными данными для прямого преобразования и входными для обратного; поскольку амплитуды комплексные, то по ним можно вычислить одновременно и амплитуду, и фазу;
— N комплексных амплитуд синусоидальных сигналов, слагающих исходный сигнал; являются выходными данными для прямого преобразования и входными для обратного; поскольку амплитуды комплексные, то по ним можно вычислить одновременно и амплитуду, и фазу;
§ 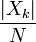 — обычная (вещественная) амплитуда k-го синусоидального сигнала;
— обычная (вещественная) амплитуда k-го синусоидального сигнала;
§ arg(Xk) — фаза k-го синусоидального сигнала (аргумент комплексного числа);
§ k — частота k-го сигнала, равная 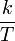 , где T — период времени, в течение которого брались входные данные.
, где T — период времени, в течение которого брались входные данные.
Из последнего видно, что преобразование раскладывает сигнал на синусоидальные составляющие (которые называются гармониками) с частотами от N колебаний за период до одного колебания за период. Поскольку частота дискретизации сама по себе равна N отсчётов за период, то высокочастотные составляющие не могут быть корректно отображены — возникает муаров эффект. Это приводит к тому, что вторая половина из N комплексных амплитуд, фактически, является зеркальным отображением первой и не несёт дополнительной информации.
Рассмотрим некоторый периодический сигнал x (t) c периодом равным T. Разложим его в ряд Фурье:
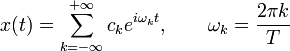
Проведем дискретизацию сигнала так, чтобы на периоде было N отсчетов. Дискретный сигнал представим в виде отсчетов: xn = x (tn), где 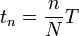 , тогда эти отсчеты через ряд Фурье запишутся следующим образом:
, тогда эти отсчеты через ряд Фурье запишутся следующим образом:
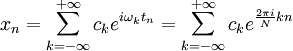
Используя соотношение: 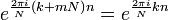 , получаем:
, получаем:
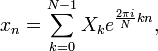 где
где 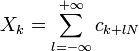
Таким образом, мы получили обратное дискретное преобразование Фурье.
Умножим теперь скалярно выражение для xn на 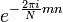 и получим:
и получим:
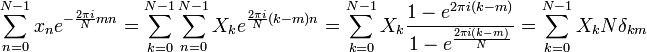
Здесь использованы: а) выражение для суммы конечного числа членов (экспонент) геометрической прогрессии, и б) выражение символа Кронекера как предела отношения функций Эйлера для комплексных чисел. Отсюда следует, что:
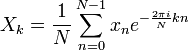
Эта формула описывает прямое дискретное преобразование Фурье.
В литературе принято писать множитель 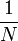 в обратном преобразовании, и поэтому обычно пишут формулы преобразования в следующем виде:
в обратном преобразовании, и поэтому обычно пишут формулы преобразования в следующем виде:
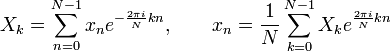
Дискретное преобразование Фурье является линейным преобразованием, которое переводит вектор временных отсчётов 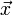 в вектор спектральных отсчётов той же длины. Таким образом, преобразование может быть реализовано как умножение квадратной матрицы на вектор:
в вектор спектральных отсчётов той же длины. Таким образом, преобразование может быть реализовано как умножение квадратной матрицы на вектор:
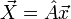
матрица А имеет вид:
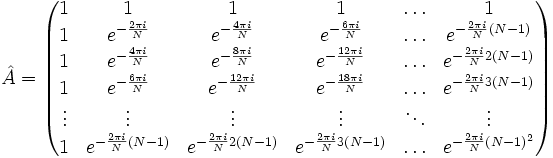
Элементы матрицы задаются следующей формулой:
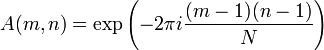
1 линейность
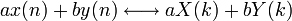
2 сдвиг по времени
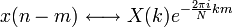
3 периодичность
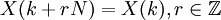
4 выполняется Теорема Парсеваля
5 обладает спектральной плотностью
S (k) = | x (k) | 2
6 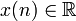
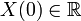
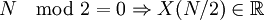
Стоит отметить, что нулевая гармоника является суммой значений сигнала.
 2015-05-06
2015-05-06 3588
3588
