Анализ цепи переменного тока с ёмкостным сопротивлением

Как известно из курса физики, совокупность двух проводников, разделенных слоем диэлектрика, называется конденсатором и представляет собой электрическую емкость.

Следовательно, всякая электрическая линия передачи (воздушная или кабельная) может рассматриваться как некоторая система конденсаторов или емкость.

Особенно большой емкостью обладают кабельные линии. Если приложить к кабелю периодически изменяющееся напряжение и оставить разомкнутым все его жилы в конце линии, то в кабеле, при его значительной длине, будут непрерывно циркулировать зарядно-разрядные токи.

При понижении напряжения заряды будут стекать с обкладок обратно к генератору.

Под влиянием сил переменного электрического поля между обкладками конденсатора в атомах диэлектрика происходит смещение электронов то в одну, то в другую сторону. Это направленное колебательное движение электронов в атомах диэлектрика представляет собой так называемый ток смещения.

Таким образом, в проводах, соединяющих генератор с конденсатором, будут циркулировать зарядный и разрядный токи проводимости, а в диэлектрике между обкладками конденсатора – токи смещения. Поэтому принято считать, что конденсатор как бы «пропускает» через себя переменный электрический ток.

Пусть к обкладкам конденсатора емкостью С (рис. 1-12, а) приложено синусоидальное напряжение . Активным и индуктивным сопротивлениями этой цепи пренебрежем, считая . Тогда при установившемся режиме через конденсатор С, как известно, будет протекать некоторый переменный ток t. Выясним форму и определим фазу этого тока и сравним их соответственно с формой и фазой приложенного напряжения и.

Мгновенное значение тока в цепи с емкостью представим равным скорости изменения электрического заряда q на обкладках конденсатора

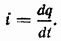
Так как 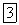и в любой момент времени напряжение на обкладках конденсатора уравновешивается приложенным напряжением и, то

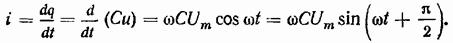
При ток i становится максимальным:

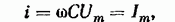
тогда

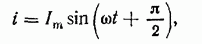
т. e. ток, как и приложенное напряжение, изменяется по закону синуса, 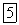опережает его по фазе на

Векторная и временная диаграммы для цепи переменного тока с емкостью приведены на рисунках 1-12, б и 1-12, в соответственно.

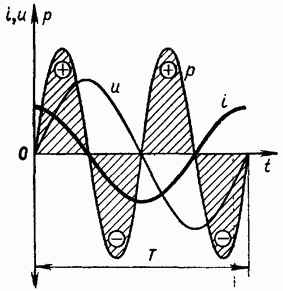
Рис. 1-13

Деля соотношение (1.22) на получим:

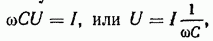
здесь — имеет размерность сопротивления и называется емкостным сопротивлением, обозначается

Соотношение представляет собой математическую запись закона Ома для цепи переменного тока с емкостью.

Найдем выражения для мгновенной и средней (активной) мощности в случае чисто емкостной цепи.

Мгновенная мощность

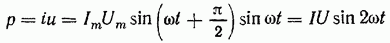
изменяется по закону синуса с удвоенной частотой (рис. 1-13). При этом положительные значения мощности (нечетные четверти периода) соответствуют потреблению энергии конденсатором (энергия запасаетсяэлектрическим полем конденсатора), отрицательные значения соответствуют возврату запасенной энергии обратно источнику.

Средняя за период мощность (активная) в этой цепи равна нулю:

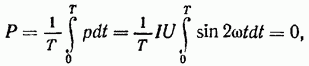
т. e. в идеализированной цепи переменного тока с конденсатором происходит лишь периодический обмен электрической энергией между источником и этим конденсатором.