Рассмотрим цепь переменного тока, состоящую из активного сопротивления R и катушки индуктивности L, соединенных последовательно (рис. 1-9, а). Такая цепь имеет существенное значение для выяснения зависимости сдвига фаз между током и напряжением от соотношения значений R и L. Кроме того, все реальные цепи, содержащие индуктивность, имеют и активное сопротивление сопротивление провода обмотки и подводящих проводов, потери в сердечниках и т. д.). Для такой цепи условие электрического равновесия (по второму закону Кирхгофа) можно записать в следующем виде:
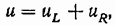
т. е. приложенное напряжение и уравновешивается суммой «ал-ря-жений на элементах цепи R и L.
Предположим, что в рассматриваемой цепи установился синусоидальный ток:
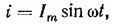
тогда напряжения на элементах R и L будут равны:
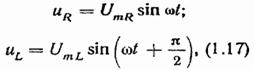
а приложенное напряжение 
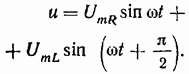
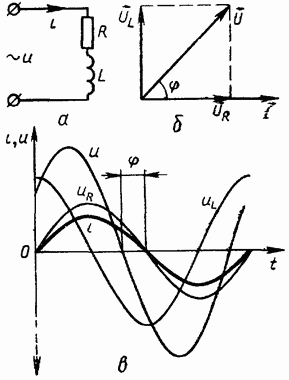
Рис. 1-9
Полученный результат (1.18) показывает, что. приложенное напряжение и также синусоидально, т. е. наше допущение (1.16) верно. Для нахождения
окончательного уравнения приложенного напряжения, которое может обеспечить предполагаемый нами ток i в цепи, построим в соответствии с соотношениями (1.16) и (1.17) векторную диаграмму (рис. 1-9, б), на которой найдем вектор приложенного напряжения 
Из полученной векторной диаграммы следует, что в рассматриваемой цепи ток 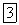 отстает по фазе от приложенного напряжения U, но не на как в случае чистой индуктивности, а на некоторый угол
отстает по фазе от приложенного напряжения U, но не на как в случае чистой индуктивности, а на некоторый угол  Причем,
Причем, 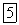 и при заданной индуктивности зависит в конечном счете от значения активного сопротивления: угол
и при заданной индуктивности зависит в конечном счете от значения активного сопротивления: угол  уменьшается с увеличением
уменьшается с увеличением 
Таким образом, для рассматриваемой цепи приложенное напряжение и следует представить в виде
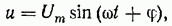
где  (из векторной диаграммы).
(из векторной диаграммы).
Временные диаграммы тока и напряжений в цепи с R и L представлены на рисунке 1-9, в.
На векторной диаграмме (рис. 1-9, б) векторы  образуют так называемый треугольник напряжений. Если все стороны этого треугольника разделить на значение тока в цепи
образуют так называемый треугольник напряжений. Если все стороны этого треугольника разделить на значение тока в цепи  то получится треугольник, подобный данному, — треугольник сопротивлений (рис. 1-10). Стороны этого треугольника не являются векторами. Это отрезки, так как сопротивления постоянны и не изменяются гармонически подобно току или напряжению.
то получится треугольник, подобный данному, — треугольник сопротивлений (рис. 1-10). Стороны этого треугольника не являются векторами. Это отрезки, так как сопротивления постоянны и не изменяются гармонически подобно току или напряжению.
Из треугольника сопротивлений (см. рис. 1-10) имеем:
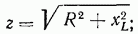
где z — полное, R — активное и  индуктивное сопротивление.
индуктивное сопротивление.
Тогда закон Ома для цепи с активным и индуктивным сопротивлениями можно представить в виде

Теперь определим угол  из соотношения
из соотношения
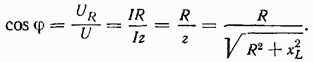
Выясним, как изменяется мощность в цепи с R и L. Поскольку мгновенные значения  можно представить как
можно представить как
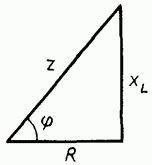
Рис. 1-10
то мгновенное значение мощности равно
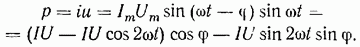
Как видно, мгновенное значение мощности имеет две составляющие: активную  и индуктивную
и индуктивную  причем обе составляющие зависят от угла сдвига фаз
причем обе составляющие зависят от угла сдвига фаз  между током и напряжением. Так, в случае
между током и напряжением. Так, в случае  цепь становится чисто активной (см. рис. 1-6) и мгновенная мощность равна
цепь становится чисто активной (см. рис. 1-6) и мгновенная мощность равна
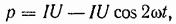
а в случае  чисто индуктивной (см. рис. 1-8).
чисто индуктивной (см. рис. 1-8).
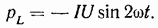
Временную диаграмму мгновенной мощности можно построить, перемножая ординаты соответствующих диаграмм тока и напряжения для каждого момента времени (рис. 1-11).
В случае  средняя за период мощность не равна нулю:
средняя за период мощность не равна нулю:
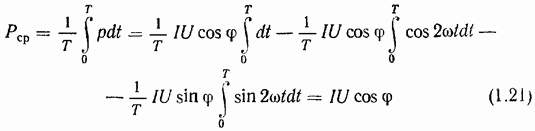
и представляет собой активную мощность. Соответствующая этой мощности электрическая энергия поступает от источника и превращается в активном сопротивлении R, например, в теплоту. В самом деле, подставив в формулу (1.21) значение  из соотношения (1.20), получим:
из соотношения (1.20), получим:
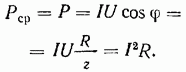
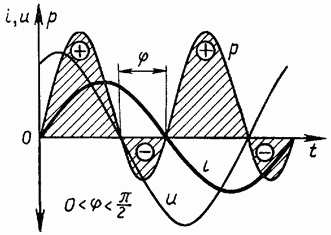
Рис. 1-11
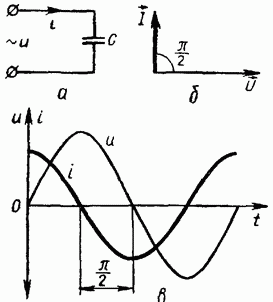
Рис. 1-12
Среднее же значение реактивной (индуктивной) составляющей мощности равно нулю:
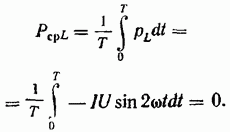
Итак, в цепи переменного тока с R и L угол сдвига фаз между током и напряжением зависит от соотношения значений R и L и изменяется в пределах 
 2015-04-08
2015-04-08 1861
1861








