В реальном колебательном контуре учитывается, что, кроме катушки индуктивностью L, конденсатора емкостью С, в цепи также имеется резистор сопротивлением R,отличным от нуля, что является причиной затухания колебаний в реальном колебательном контуре. Свободные затухающие колебания – колебания, амплитуда которых из-за потерь энергии реальной колебательной системой с течением времени уменьшается.
Для цепи реального колебательного контура напряжения на последовательно включенных конденсаторе емкостью С и резисторе сопротивлением R складываются. Тогда с учетом закона Фарадея для цепи реального колебательного контура можно записать:
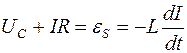 ,
,
где 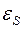 – электродвижущая сила самоиндукции в катушке;
– электродвижущая сила самоиндукции в катушке;
UC – напряжение на конденсаторе (UC =q/C);
IR – напряжения на резисторе.
Исходя из того, что I=dq/dt, получаем дифференциальное уравнение свободных затухающих гармонических колебаний величины заряда q на обкладках конденсатора:
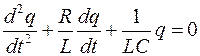 или
или  ,
,
где 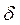 – коэффициент затухания колебаний (
– коэффициент затухания колебаний (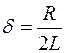 ),
), 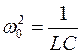 .
.
Решением полученного дифференциального уравнения является функция q (t), то есть уравнение свободных затухающих гармонических колебаний величины заряда q на обкладках конденсатора:
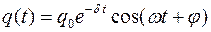 ,
,
где q (t) – величина заряда на обкладках конденсатора в момент времени t;
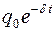 – амплитуда затухающих колебаний заряда на обкладках конденсатора в момент времени t;
– амплитуда затухающих колебаний заряда на обкладках конденсатора в момент времени t;
q 0 – начальная амплитуда затухающих колебаний заряда на обкладках конденсатора;
 – круговая (или циклическая) частота колебаний (
– круговая (или циклическая) частота колебаний (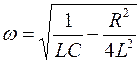 );
);
 – фаза затухающих колебаний в момент времени t;
– фаза затухающих колебаний в момент времени t;
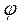 – начальная фаза затухающих колебаний.
– начальная фаза затухающих колебаний.
Тема 8. Электромагнитные волны. Вектор Умова-Пойнтинга
Согласно теории Максвелла электромагнитные поля могут существовать в виде электромагнитных волн, фазовая скорость 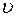 распространения которых определяется выражением:
распространения которых определяется выражением:
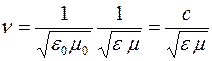 ,
,
где 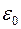 и
и 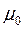 – соответственно электрическая и магнитная постоянные,
– соответственно электрическая и магнитная постоянные,
e и m – соответственно электрическая и магнитная проницаемости среды,
с – скорость света в вакууме (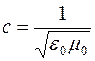 ).
).
В вакууме (e = 1, m = l) скорость распространения электромагнитных волн совпадает со скоростью света(с), что согласуется с теорией Максвелла о том,
что свет представляет собой электромагнитные волны.
По теории Максвелла электромагнитные волны являются поперечными, то есть векторы 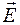 и
и 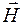 напряженностей электрического и магнитного полей взаимно перпендикулярны и лежат в плоскости, перпендикулярной вектору
напряженностей электрического и магнитного полей взаимно перпендикулярны и лежат в плоскости, перпендикулярной вектору 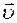
скорости распространения волны, причем векторы 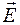 ,
,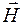 и
и 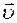 образуют правовинтовую систему (рис. 19).
образуют правовинтовую систему (рис. 19).

Из теории Максвелла следует также, что в электромагнитной волне векторы 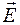 и
и 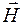 колеблются в одинаковых фазах (рис. 19), то есть значения напряженностей Е и Н электрического и магнитного полей одновременно достигают максимума и одновременно обращаются в нуль, причем мгновенные значения Е и Н связаны соотношением:
колеблются в одинаковых фазах (рис. 19), то есть значения напряженностей Е и Н электрического и магнитного полей одновременно достигают максимума и одновременно обращаются в нуль, причем мгновенные значения Е и Н связаны соотношением:
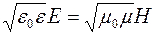 .
.
Уравнение плоской монохроматической электромагнитной волны (индексы у и z при Е и Н подчеркивают лишь то, что векторы 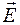 и
и 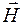 направлены вдоль взаимно перпендикулярных осей в соответствии с рис. 19):
направлены вдоль взаимно перпендикулярных осей в соответствии с рис. 19):
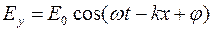 ,
,
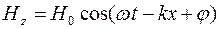 ,
,
где E 0 и Н 0– соответственно амплитуды напряженностей электрического и магнитного полей,
w – круговая частота волны, 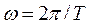 (T – период колебаний),
(T – период колебаний),
k – волновое число, 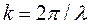 (
(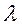 – длина волны),
– длина волны),
j – начальная фаза колебаний (начальная фаза колебаний j имеет одинаковое значение как для колебания электрического, так и магнитного векторов, так как в электромагнитной волне эти колебания происходят в одинаковых фазах).
Энергия электромагнитных волн. Электромагнитные волны переносят энергию. Объемная плотность w энергии электромагнитной волны складывается из объемных плотностей wэл электрического и wм магнитного полей:
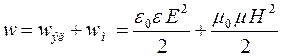 .
.
Учитывая выражение связи между величинами Е и Н, можно получить, что суммарная плотность энергии электрического и магнитного полей:
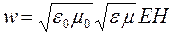 .
.
Умножив плотность энергии w на скорость 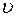 распространения волны в среде, получим модуль плотности потока энергии:
распространения волны в среде, получим модуль плотности потока энергии:
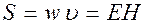 .
.
Tax как векторы 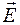 и
и 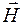 взаимно перпендикулярны, то произведение EH совпадает с модулем вектора
взаимно перпендикулярны, то произведение EH совпадает с модулем вектора 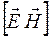 (
(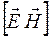 – векторное произведение векторов
– векторное произведение векторов 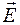 и
и 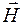 ). Кроме того, направление вектора
). Кроме того, направление вектора 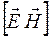 совпадает с направлением распространения волны, то есть с направлением переноса энергии, что позволило ввести в ектор
совпадает с направлением распространения волны, то есть с направлением переноса энергии, что позволило ввести в ектор 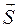 , равныйвекторному произведению
, равныйвекторному произведению 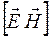 , как вектор плотности потока электромагнитной энергии, называемый вектором Умова – Пойнтинга:
, как вектор плотности потока электромагнитной энергии, называемый вектором Умова – Пойнтинга:
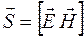 .
.
Модуль в ектора 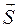 равен энергии, переносимой электромагнитной волной за единицу времени через единичную площадку, перпендикулярную направлению распространения волны.
равен энергии, переносимой электромагнитной волной за единицу времени через единичную площадку, перпендикулярную направлению распространения волны.
 2014-02-02
2014-02-02 3681
3681
