Лекция 3. Прямолинейные колебания точки
В данной лекции рассматриваются следующие вопросы:
1. Свободные колебания без учета сил сопротивления.
2. Понятие о фазовой плоскости.
3. Свободные колебания в поле постоянной силы.
4. Параллельное включение упругих элементов.
5. Последовательное включение упругих элементов.
6. Вынужденные колебания. Резонанс.
7. Свободные колебания с вязким сопротивлением.
8. Вынужденные колебания с вязким сопротивлением.
Изучение данных вопросов необходимо для динамики колебательного движения механических систем, теории удара, для решения задач в дисциплинах «Сопротивление материалов» и «Детали машин».
Свободные колебания без учета сил сопротивления.
Учение о колебаниях составляет основу ряда областей физики и техники. Хотя колебания, рассматриваемые в различных областях, например в механике, радиотехнике, акустике и др., отличаются друг от друга по своей физической природе, основные законы этих колебаний во всех случаях остаются одними и теми же. Поэтому изучение механических колебаний является важным не только по той причине, что такие колебания очень часто имеют место в технике, но и вследствие того, что результаты, полученные при изучении механических колебаний, могут быть использованы для изучения и уяснения колебательных явлений в других областях.
Начнем с изучения свободных колебаний точки без учета сил сопротивления. Рассмотрим точку М, движущуюся прямолинейно под действием одной только восстанавливающей силы 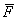 , направленной к неподвижному центру О и пропорциональной расстоянию от этого центра. Проекция силы
, направленной к неподвижному центру О и пропорциональной расстоянию от этого центра. Проекция силы 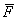 на ось Ох (рис.27) будет равна
на ось Ох (рис.27) будет равна
Fx=-cx.
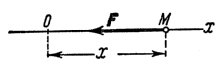
Рис.27
Сила 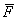 , как видим, стремится вернуть точку в равновесное положение О, где
, как видим, стремится вернуть точку в равновесное положение О, где 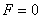 ; отсюда и наименование «восстанавливающая» сила. Примером такой силы является сила упругости. Коэффициент c пропорциональности называется жесткостью упругого элемента.
; отсюда и наименование «восстанавливающая» сила. Примером такой силы является сила упругости. Коэффициент c пропорциональности называется жесткостью упругого элемента.
Найдем закон движения точки М. Составляя дифференциальное уравнение движения получим
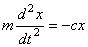 .
.
Деля обе части равенства на т и вводя обозначение
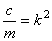 ,
,
приведем уравнение к виду
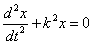 .
.
Уравнение представляет собою дифференциальное уравнение свободных колебаний при отсутствии сопротивления. Решение этого линейного однородного дифференциального уравнения второго порядка ищут в виде x=ent. Полагая x=ent, получим для определения п так называемое характеристическое уравнение, имеющее в данном случае вид п2 + k2 = 0. Поскольку корни этого характеристического уравнения являются чисто мнимыми (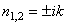 ), то, как известно из теории дифференциальных уравнений, общее решение имеет вид
), то, как известно из теории дифференциальных уравнений, общее решение имеет вид
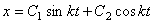 ,
,
где C 1 и С 2 - постоянные интегрирования. Если вместо постоянных C 1 и С 2 ввести постоянные а и 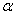 , такие, что
, такие, что 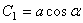 ,
, 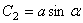 , то мы получим
, то мы получим 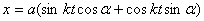 или
или 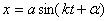 .
.
Это другой вид решения, в котором постоянными интегрирования являются а и 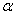 . Им удобнее пользоваться для общих исследований.
. Им удобнее пользоваться для общих исследований.
Скорость точки в рассматриваемом движении равна
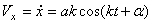 .
.
Колебания, совершаемые точкой по закону 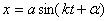 называются гармоническими колебаниями.
называются гармоническими колебаниями.
Всем характеристикам этого движения можно дать наглядную кинематическую интерпретацию. Рассмотрим точку В, движущуюся равномерно по окружности радиуса а из положения В 0 определяемого углом 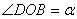 (рис.28).
(рис.28).
Пусть постоянная угловая скорость вращения радиуса ОВ равна k. Тогда в произвольный момент времени t угол 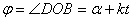 и проекция М точки В на диаметр, перпендикулярный к DE, движется по закону
и проекция М точки В на диаметр, перпендикулярный к DE, движется по закону 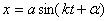 , где х=ОМ, т.е. совершает гармонические колебания.
, где х=ОМ, т.е. совершает гармонические колебания.
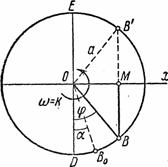
Рис.28
Величина а, равная наибольшему отклонению точки М от центра колебаний, называется амплитудой колебаний. Величина 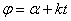 называется фазой колебаний.
называется фазой колебаний.
Величина k, совпадающая с угловой скоростью вращения радиуса ОВ, показанного на рис.15 называется круговой частотой колебаний.
Промежуток времени Т (или 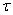 ), в течение которого точка совершает одно полное колебание, называется периодом колебаний.
), в течение которого точка совершает одно полное колебание, называется периодом колебаний.
По истечении периода фаза изменяется на 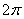 . Следовательно, должно
. Следовательно, должно 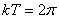 откуда период
откуда период
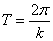 .
.
Величина 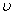 , обратная периоду и определяющая число колебаний, совершаемых за одну секунду, называется частотой колебаний
, обратная периоду и определяющая число колебаний, совершаемых за одну секунду, называется частотой колебаний
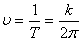 .
.
Отсюда видно, что величина k отличается от Т только постоянным множителем 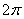 . В дальнейшем мы обычно для краткости частотой колебаний будем называть величину k.
. В дальнейшем мы обычно для краткости частотой колебаний будем называть величину k.
Значения а и 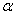 определяются по начальным условиям. Считая при t =0
определяются по начальным условиям. Считая при t =0 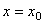 ,
, 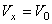 получим
получим 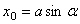 и
и 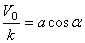 . Отсюда, складывая сначала квадраты этих равенств,а затем деля их почленно, найдем:
. Отсюда, складывая сначала квадраты этих равенств,а затем деля их почленно, найдем:
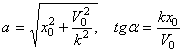 .
.
Отметим, что свободные колебания при отсутствии сопротивления обладают следующими свойствами: 1) амплитуда и начальная фаза колебаний зависят от начальных условий; 2) частота k, а следовательно, и период Т колебаний от начальных условий не зависят.
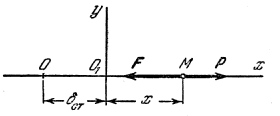
Рис.29
Влияние постоянной силы на свободные колебания точки. Пусть на точку М, кроме восстанавливающей силы F, направленной к центру О, действует еще постоянная по модулю и направлению сила Р (рис.29). Величина силы F по прежнему пропорциональна расстоянию от центра О, т.е. 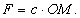
Очевидно, что в этом случае положением равновесия точки М будет центр О 1 отстоящий от О на расстоянии 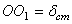 , которое определяется равенством
, которое определяется равенством 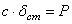 или
или
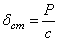 .
.
Величину 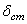 назовем статическим отклонением точки. Примем центр O 1 за начало отсчета и направим координатную ось О 1 х в сторону действия силы
назовем статическим отклонением точки. Примем центр O 1 за начало отсчета и направим координатную ось О 1 х в сторону действия силы 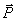 . Тогда
. Тогда 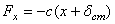 ,
, 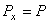 . В результате, составляя дифференциальное уравнение движения и учитывая, что согласно равенству
. В результате, составляя дифференциальное уравнение движения и учитывая, что согласно равенству 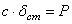 , будем иметь:
, будем иметь:
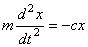 или
или 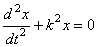 .
.
Отсюда заключаем, что постоянная сила Р не изменяет характера колебаний, совершаемых точкой под действием восстанавливающей силыF, а только смещает центр этих колебаний в сторону действия силы Р на величину статического отклонения 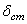 .
.
 2015-05-06
2015-05-06 2129
2129