Потенциальная энергия равна потенциальной функции с обратным знаком, значит, является функцией только координат и не зависит от скоростей и ускорений

Отсюда следует, что 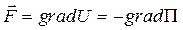, т.е. сила как градиент направлена в сторону возрастания потенциальной функции 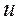, но в сторону убывания потенциальной энергии, т.е. в сторону убывания потенциала.

с) Закон сохранения механической энергии.

Пусть внешние и внутренние силы потенциальны, тогда по теореме о кинетической энергии в дифференциальной форме:

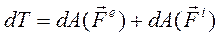(182)

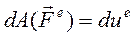(183)

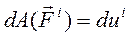(184)

По определению потенциального поля:

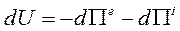(185)

Отсюда:

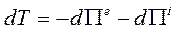(186)

Или:

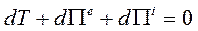(187)

Внесем под знак дифференциала:

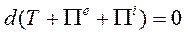(188)

Отсюда:

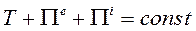(189)

Закон сохранения механической энергии. Это равенство называется интегралом движения:

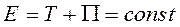(190)

Формулировка:

Если все силы системы потенциальны и потенциал не зависит от времени, то при движении механической системы ее полная механическая энергия остается величиной постоянной. Полная механическая энергия это сумма кинетической и потенциальной энергий. Это означает, что механическая энергия сохраняется не только в замкнутых системах, но и при воздействии внешних сил, если они потенциальны. Силы и системы сил, для которых выполняется закон сохранения энергии, называются консервативными.

6 ДИНАМИКА ДВИЖЕНИЯ ТВЕРДОГО ТЕЛА

Рассматриваемые вопросы:

Динамика простейших движений твердого тела: дифференциальные уравнения поступательного, вращательного и плоскопараллельного движения твердого тела. Дифференциальные уравнения движения системы материальных точек.

6.1 Основные задачи динамики твердого тела

Решение задач динамики твердого тела встречаются две основные группы задач. К первой группе относятся задачи, в которых по заданным уравнениям движения твердого тела требуется определить систему сил, под действием которых происходит это движение. Ко второй относятся задачи, в которых по заданным силам, действующим на тело, требуется при определенных начальных условиях определить уравнение движения центра масс, а для несвободного тела найти также реакции связей.

Рассмотрим движение твердого тела в плоскости. Для определения его положения требуется задать три независимых между собой параметра, обычно это координаты центра масс x_c, y_c и угол поворота φ, которые полностью определяют положение твердого тела в плоскости.

Движение тела в плоскости обычно раскладываются на простейшие: поступательное движение тела, задаваемое уравнениями движения центра масс x_c = x_c(t), y_c = y_c(t) и вращение тела вокруг оси, проходящей через центр масс тела, задаваемое уравнением φ = φ(t).

Для получения законов движения можно воспользоваться теоремой о движении центра масс и теоремой об изменении кинетического момента.

Согласно теореме о движении центра масс получим:

, т.е. в проекциях ; ;

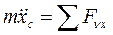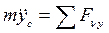Согласно теореме об изменении кинетического момента относительно оси вращения получим:

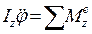(191)

Законы движения тела в плоскости имеют вид:

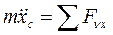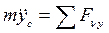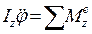; ; (192)

6.2 Дифференциальные уравнения движения твёрдого тела

а)Дифференциальные уравнения поступательного движения твёрдого тела

Для того, чтобы твердое тело двигалось поступательно, линия действия главного вектора внешних сил механической системы должна проходить через центр масс тела.

Так как, по определению, при поступательном движении все точки тела движутся одинаково (т.е. имеют равные скорости, ускорения и совпадающие при наложении траектории), то для изучения поступательного движения твёрдого тела достаточно знать движение какой-либо одной точки тела. Это может быть и центр масс.

Спроецировав теорему о движении центра масс на координатные оси x, y, z получим три скалярных уравнения:

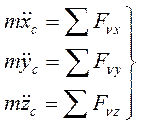(193)

Дифференциальный закон движения точки в пространстве (или в плоскости) в общем случае позволяет решить две основные задачи динамики.

б) Дифференциальные уравнения вращательного движения твёрдого тела

Твердое тело, вращающееся вокруг неподвижной оси, является примером несвободного твердого тела. Следовательно, при изучении его движения необходимо отбросить связи, заменив его реакциями связей, рассматривать твердое тело как свободное.

Дифференциальное уравнение вращательного движения твёрдого тела имеет вид:

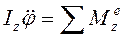(194)

где I_z – момент инерции тела относительно оси вращения z;

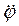– угловое ускорение тела;

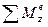– сумма моментов внешних сил относительно оси вращения.

Реакции подшипников считаем внешними силами, которые не создают моменты относительно оси вращения, т.к. линии их действия пересекают эту ось.

Дифференциальное уравнение вращательного движения тела при известном моменте инерции относительно оси вращения I_z позволяет решать следующие задачи:

1. Зная закон движения тела φ = φ(t),можно определить момент внешней силы, действующей на тело, или силу, создающую этот момент.

2. Зная момент внешних сил, приложенных к телу, и начальные условия φ(0) = φ₀, ω(0) = ω₀, определить закон вращательного движения тела.

в) Дифференциальные уравнения плоскопараллельного движения твёрдого тела

При плоском движении все точки твердого тела движутся в параллельных плоскостях. Поэтому достаточно рассмотреть движение какого-либо сечения тела в одной плоскости.

Дифференциальные уравнения плоского движения твёрдого тела имеют вид:

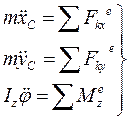(195)

Где: m – масса тела;

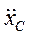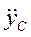, – проекции ускорения центра масс на оси координат;

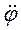– угловое ускорение тела;

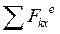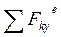, – сумма проекций внешних сил на соответствующие оси координат;

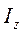– момент инерции тела относительно оси, проходящей через центр масс и перпендикулярной плоскости движения тела;

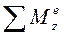– сумма моментов внешних сил относительно той же оси.

Интегрируя эти уравнения, можно определить X_C _, Y_C и j как функции времени. Для определения постоянных интегрирования используются начальные условия движения: координаты центра масс и угол поворота тела в начальный момент времени, а также проекции начальной скорости центра масс на оси координат и начальная угловая скорость тела.

Если тело совершает несвободное движение, то в число внешних сил следует включить реакции связей.

7 Основы аналитической механики

Рассматриваемые вопросы:

Виды аналитических связей: односторонние и двухсторонние, кинематические и геометрические, стационарные и нестационарные, голономные и неголономные, идеальные и неидеальные. Уравнения аналитических связей. Вариация и дифференциал. Перемещения возможные и действительные. Виртуальная работа силы и момента силы. Постулат идеальных связей. Принцип возможных перемещений, принцип возможных скоростей (принцип Лагранжа).