Относительное движение точки

Уравнения относительного движения и покоя точки

Законы динамики и полученные из них в предыдущих главах урав­нения и теоремы верны только для так называемого абсолютного движения точки, т. е. движения по отношению к инерциальной (неподвижной) системе отсчета.

Эта глава посвящена изучению относительного движения точки, т. е. движения по отношению к неинерциальным, произвольно дви­жущимся системам отсчета. Рассмотрим материальную точку М, движущуюся под действием приложенных к ней сил 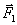, , 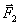… 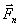_, являющихся результатом взаимодействия точки с другими материальными телам.

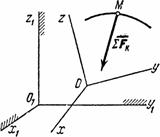
Рис.11

Будем изу­чать движение этой точки по отношению к осям Oxyz (рис.11),которые в свою очередь каким-то извест­ным нам образом движутся относительно неподвижных осей 0₁x₁y₁z₁. Найдем зависимость между относи­тельным ускорением точки а_отн и дейст­вующими на нее силами. Для абсолютного

Рисунок.11

движения основной закон динамики имеет вид 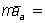Σ .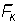

Но из кинематики известно, что 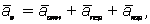где 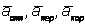-относительное, переносное и кориолисово ускорения точки. Подставляя это значение а_а и считая в дальнейшем 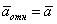, так как эта величина представляет собою ускорение изучаемого нами относительного движения, получим:

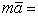Σ .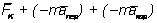

Введем обозначения: .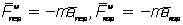

Величины 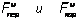по размерности являются силами. Назовем их соответственно переносной и кориолисовой силами инерции. Тогда предыдущее уравнение примет вид

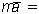Σ .

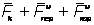Уравнение выражает основной закон динамики для отно­сительного движения точки: все уравнения и теоремы механики для относительного движения точки составляются так же, как уравнения абсолютного движения, если при этом к действующим на точку силам взаимодействия с другими телами прибавить переносную и кориолисову силы инерции. Прибавление сил 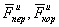учитывает влияние на относительное движение точки перемещения подвижных осей.

Рассмотрим некоторые частные результаты.

1. Если подвижные оси движутся поступательно, то 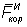=0, так как в этом случае ω=0 (ω-угловая скорость вращения подвиж­ных осей Oxyz) и закон относительного движения принимает вид

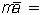Σ .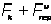

2. Если подвижные оси перемещаются поступательно, равномерно и прямолинейно, то 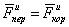=0 и закон относительного движе­ния будет иметь такой же вид, как и закон движения по отношению к неподвижным осям. Следовательно, такая система отсчета также будет инерциальной.

Из полученного результата вытекает, что никаким механическим экспериментом нельзя обнаружить, находится ли данная система от­счета в покое или совершает поступательное, равномерное и прямо­линейное движение. В этом состоит открытый еще Галилеем принцип относительности классической механики.

1. Если точка по отношению к подвижным осям находится в по­кое, то 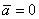и 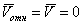, а следовательно, 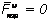, так как кориолисово ускорение 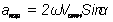. Тогда:

Σ .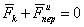

Уравнение представляет собою уравнение относительного равновесия (покоя) точки. Из него следует, что уравнения отно­сительного равновесия составляются так же, как уравнения равновесия в неподвижных осях, если при этом к действующим на точку силам взаимодействия с другими телами добавить переносную силу инерции.

Влияние вращения Земли на равновесие и движение тел.

При решении большинства технических задач мы считаем си­стему отсчета, связанную с Землей, неподвижной (инерциальной). Тем самым мы не учитываем суточное вращение Земли и ее движение по орбите вокруг Солнца. Таким образом, считая систему отсчета, связанную с Землей, инерциальной, мы по существу прене­брегаем ее суточным вращением вместе с Землей по отноше­нию к звездам. Это вращение происходит со скоростью: 1 оборот за 23 часа 56 минут 4 секунды, т. е. с угловой скоростью

.

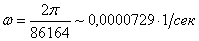Исследуем, как сказывается такое довольно медленное вращение на равновесии и движении тел.

1. Относительный покой на поверхности Земли. Сила тяжести. Рассмотрим материальную точку, лежащую на неподвижной относительно Земли гладкой «горизонтальной» плоскости (рис.12). Условие ее равновесия по отношению к Земле состоит в том, что 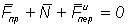, где 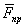-сила притяжения Земли, N -реакция плоскости, 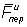-переносная сила инерции. Так как ω=const, то сила 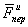имеет только нормальную составляющую, направленную перпендикулярно к оси вра­щения Земли. Сложим силы 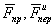и введем обозначение

.

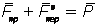Тогда на точку М будут действовать две силы 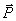и 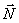, уравно­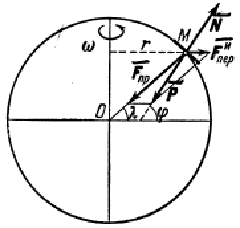 вешивающие друг друга. Сила 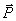и представляет собою ту силу, ко­торую мы называем силой тяжести.

На­правление силы 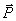будет направлением верти­кали в данном пункте поверхности, а плоскость, перпендикулярнаяк 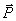и будет горизонтальной плоскостью. По модулю 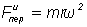(r- расстояние точки М от земной оси) и величина малая по сравнению с F_пр, так как величина ω² очень мала. Направление силы 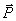мало отличается от направления F_пр.

При взвешивании тел мы определяем силу 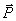, т.к. именно с такой силой тело давит на тело весов. То есть, вводя в уравнения равновесия силу тяжести 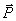, мы вводим в них и силу 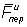, т. е. фак­тически учитываем влияние вращения Земли.

Рис.12

Поэтому при состав­лении уравнений равновесия тел по отношению к Земле ника­ких поправок на вращение Земли вводить не надо. В этом смысле равновесие по отношению к Земле можно считать абсолютным.

а) Движение по земной поверхности. При движении точки по меридиану в северном полушарии с севера на юг кориолисово ускорение 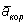направлено на восток, а сила 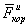- на запад. При движении с юга на север сила 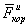будет, очевидно, направлена на восток. В обоих случаях, как мы видим, эта сила будет отклонять точку

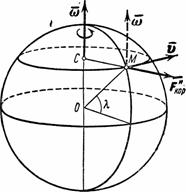
вправо от направления ее движения. Если точка движется по параллели на восток, то ускорение 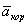будет направлено вдоль радиуса МС параллели (рис.13), а сила 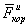в противоположную сторону. Вертикальная составляющая этой силы (вдоль ОМ) будет несколько изменять вес тела, а горизонтальная составляю­щая будет направлена к югу и будет отклонять точку тоже вправо от на­правления движения. Аналогичный ре­зультат получим при движении по па­раллели на запад.

Отсюда заключаем, что в север­ном полушарии тело, движущееся вдоль земной поверхности по любо­му направлению будет вследствие вращения Земли отклоняться вправо от направления движения. В южном полушарии отклонение будет происхо­дить влево.

Этим обстоятельством объясняется то, что реки, текущие в северном по­лушарии, подмывают правый берег (закон Бэра). В этом же при­чина отклонений ветров постоянного направления (пассаты) и мор­ских течений.