2015-04-30
1311
Рассмотрим элемент в виде прямоугольного параллелепипеда, грани которого являются главными площадками (Рис.6). Рассмотрим семейство площадок, параллельных направлению главного напряжения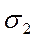 
. Выделим из параллелепипеда плоскостью, наклонённой под углом 
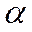к вертикальной грани, треугольную призму (Рис.6). На наклонной грани призмы действуют нормальное напряжение 
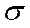и касательное напряжение 
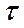. Выразим их через главные напряжения. Составим уравнения равновесия для призмы.
Рис.6
Проектируя на направление нормали к площадке, получим
.
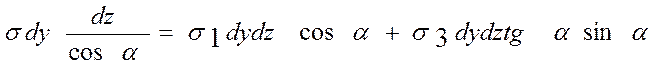Проектируя на направление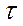 
, имеем
.
После очевидных сокращений и перехода к функциям аргумента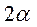 
получим:
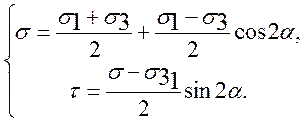(1.7)
Если рассматривать 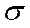и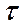 
как координаты соответствующей координатной плоскости, то можно обнаружить, что (7) представляют собой параметрические уравнения окружности. На самом деле:
.
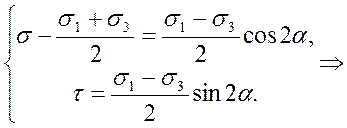
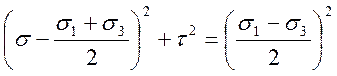Последнее соотношение представляет собой уравнение окружности, центр которой лежит на оси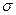 
и имеет координату 
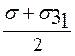. Радиусом окружности 
.
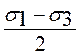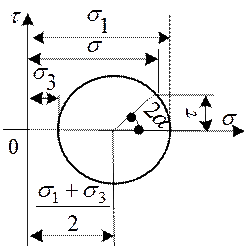Полученный круг называется круговой диаграммой Мора. Если не принимать во внимание знак касательного напряжения, то можно ограничиться построением только верхней половины круга Мора.
|
|
|
Построенная диаграмма имеет следующий смысл: каждой площадке параллельной направлению напряжения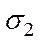 
соответствует точка на окружности.
Можно построить круговые диаграммы и для площадок параллельных направлению главных напряжени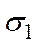й 
и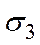 
. См. рисунок.
Площадкам общего положения, не параллельным ни одному из главных напряжений, соответствуют точки расположенные в заштрихованной области.
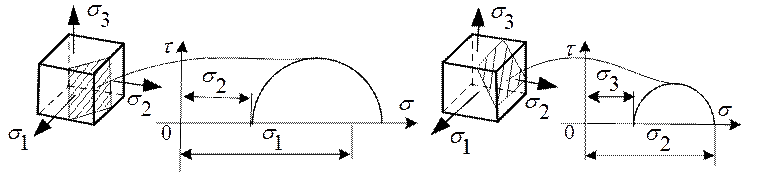
Наложим круговые диаграммы на один чертеж
