Если каждому возможному значению случайной величины X соответствует одно возможное значение случайной величины Y, то Y называют функцией случайного аргумента X: Y = j(X).
Если X – дискретная случайная величина имеет закон распределения 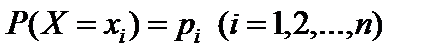 , тогда функция
, тогда функция 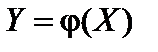 имеет значения
имеет значения 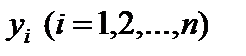 , найденные по следующей формуле:
, найденные по следующей формуле:
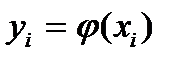 (74)
(74)
с теми же вероятностями, т. е. 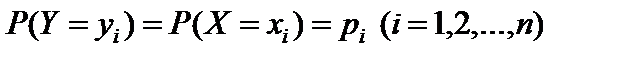 .
.
Если некоторым различным значениям xi будут соответствовать равные значения yi, то следует складывать вероятности повторяющихся значений Y.
Если X – непрерывная случайная величина, заданная дифференциальной функцией f (x), и если 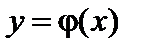 – дифференцируемая строго возрастающая или строго убывающая функция, обратная функция которой
– дифференцируемая строго возрастающая или строго убывающая функция, обратная функция которой 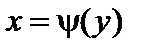 , то дифференциальная функция g (y) случайной величины Y находится по равенству:
, то дифференциальная функция g (y) случайной величины Y находится по равенству:
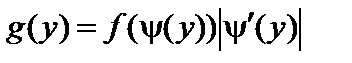 . (75)
. (75)
Если функция 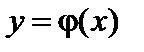 кусочно монотонная, то следует разбить интервал возможных значений X на такие интервалы, где функция
кусочно монотонная, то следует разбить интервал возможных значений X на такие интервалы, где функция 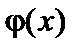 монотонна, и найти gi (y) для каждого интервала:
монотонна, и найти gi (y) для каждого интервала:
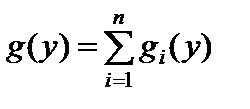 . (76)
. (76)
Пример 2.28. Найти закон распределения случайной величины
Y = X 4, если дискретная случайная величина Х задана следующим законом распределения:
| Х | –1 | –2 | ||
| Р | 0,3 | 0,1 | 0,2 | 0,4 |
Решение. Найдем возможные значения Y:
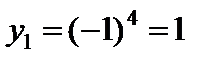 ;
; 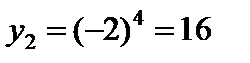 ;
; 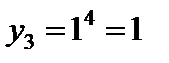 ;
; 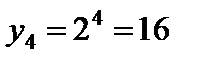 .
.
Так как 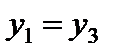 и
и 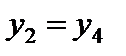 , следовательно
, следовательно
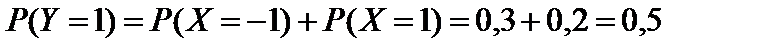 ;
;
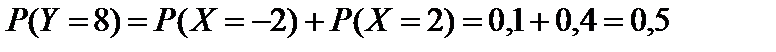 .
.
Искомый закон распределения величины Y можно представить в виде таблицы
| Y | ||
| Р | 0,5 | 0,5 |
Пример 2.29. Задана дифференциальная функция f (x) случайной величины X, возможные значения которой заключены в интервале (1; 3). Найти дифференциальную функцию случайной величины
Y = 3 X + 1.
Решение. Так как функция y = 3 x + 1 является дифференцируемой и строго возрастает, следовательно
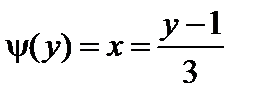 ;
; 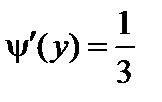 .
.
Найдем 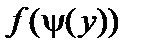 :
:
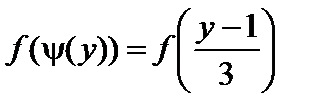 .
.
Искомая дифференциальная функция:
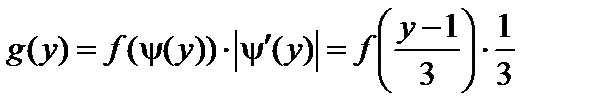 .
.
Так как х изменяется в интервале (1; 3) и y = 3 x + 1, то 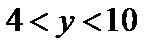 .
.
Ответ: 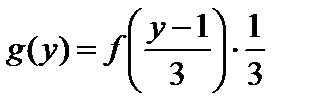 ;
; 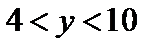 .
.
Пример 2.30. Найти распределение функции Y = X 3, если случайная величина X распределена нормально и ее математическое ожидание равно 0.
Решение. Так как функция y = x 3 дифференцируема и строго возрастает, то можно применить формулу (75).
Функция 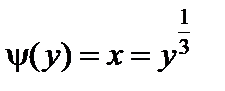 обратная функции y = x 3. Найдем
обратная функции y = x 3. Найдем 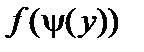 .
.
По условию 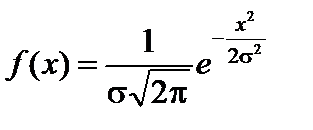 , поэтому:
, поэтому:
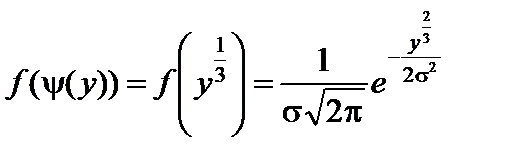 ,
, 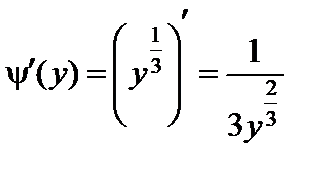 .
.
Ответ: 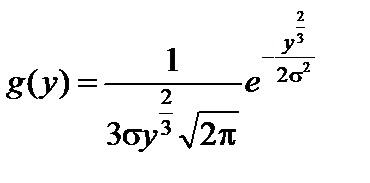 .
.
Пример 2.31. Найти математическое ожидание функции Y = j(X) =
= X 2 + 1, если дискретная случайная величина X задана следующим законом распределения:
| Х | |||
| Р | 0,2 | 0,5 | 0,3 |
Решение. Найдем возможные значения Y:
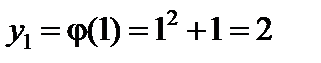 ;
; 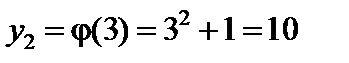 ;
; 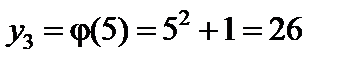 .
.
Следовательно, закон распределения величины Y можно представить в виде таблицы
| Y | |||
| P | 0,2 | 0,5 | 0,3 |
Используя формулу 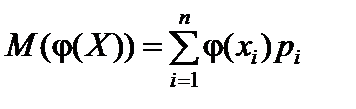 найдем математическое ожидание заданной функции:
найдем математическое ожидание заданной функции: 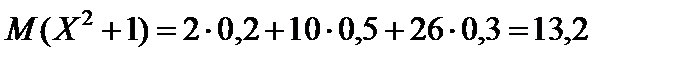 .
.
Ответ: М (Х 2 +1) = 13,2.
Пример 2.32. Найти математическое ожидание функции Y = j(X) =
= X 2, если непрерывная случайная величина X задана дифференциальной функцией распределения f (x) = sin x в интервале 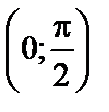 ; f (x) = 0 вне этого интервала.
; f (x) = 0 вне этого интервала.
Решение. 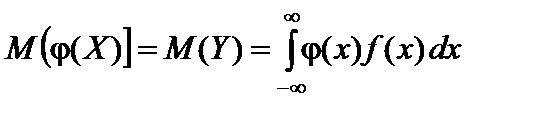 ;
; 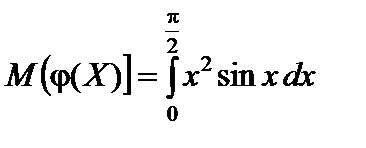 .
.
Интегрируя по частям, получим: 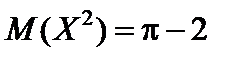 .
.
Ответ: 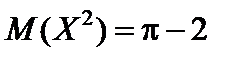 .
.
 2015-04-20
2015-04-20 2386
2386
