Система двух случайных величин

Двумерной называют случайную величину (X; Y), возможные значения которой есть пары чисел (x; y).

Случайные величины X и Y, рассматриваемые совместно, образуют систему двух случайных величин. Каждую из величин X и Y называют составляющей (компонентой).

Общей характеристикой двумерной случайной величины является функция распределения вероятностей, которая представляет собой вероятность события (X < x, Y < y); F (x, y) = P (X < x, Y < y).

Различают дискретные (составляющие этих величин дискретны) и непрерывные (составляющие этих величин непрерывны) двумерные случайные величины.

Законом распределения дискретной двумерной случайной величины называютперечень возможных значений этой величины(т. е. пар чисел)(x_i; y_i)и их вероятностей p (x_i; y_j)(i = 1, 2, …, n; j = 1, 2, …, m).

Закон распределения двумерной случайной величины может быть задан в виде таблицы с двойным входом, содержащей возможные значения и их вероятности, а также аналитически, например, в виде функции распределения.

Зная закон распределения двумерной дискретной величины, можно найти законы распределения каждой из составляющих.

Например, события (X = x ₁, Y = y ₁), (X = x ₁, Y = y ₂), …, (X = x ₁, Y =
= y_m) несовместны, поэтому

.

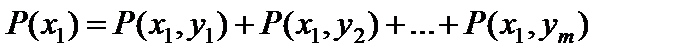Таким образом, вероятность того, что X примет значение x_i, равна сумме вероятностей столбца x_i. Аналогично, сложив вероятности строки y_j, получим вероятность P (Y = y_j).

Пример 3.1. Найти законы распределения составляющих двумерной случайной величины, заданной законом распределения в виде следующей таблицы:

X Y	x 1	x 2	x 3
y 1	0,10	0,30	0,20
y 2	0,06	0,18	0,16

Решение. Сложив вероятности по столбцам, получим вероятности возможных значений X: P (x ₁) = 0,16; P (x ₂) = 0,48; P (x ₃) = 0,36.

Запишем закон распределения составляющей X в форме таблицы:

X	x 1	x 2	x 3
P	0,16	0,48	0,36

Проверка: 0,16 + 0,48 + 0,36 = 1.

Сложив вероятности по строкам, получим вероятности возможных значений Y: P (y ₁) = 0,60; P (y ₂) = 0,40.

Запишем закон распределения составляющей Y в виде следующей таблицы:

Y	y 1	y 2
P	0,60	0,40

Проверка: 0,60 + 0,40 = 1.

3.1. Условные законы распределения вероятностей
составляющих дискретной двумерной случайной величины

Условным распределением составляющей X при Y = y_j называют совокупность условных вероятностей P (x ₁½ y_j), P (x ₂½ y_j), …, P (x_n ½ y_j), вычисленных в предположении, что событие Y = y_j (j имеет одно и то же значение при всех возможных значениях X) уже наступило.

Аналогично определяется условное распределение составляющей Y.

Условный закон распределения X в предположении, что событие
Y = y ₁ уже произошло, может быть найден по следующей формуле:

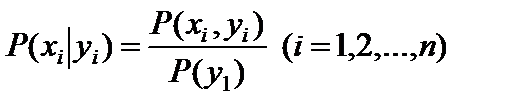. (77)

В общем случае условные законы для составляющей X могут быть представлены в виде формуле

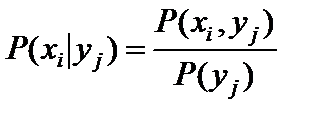. (78)

Для составляющей Y условные законы определяются формулой

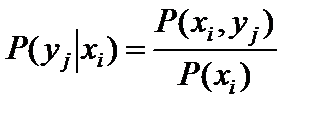. (79)

Пример 3.2. Найти условный закон распределения составляющей X при условии, что составляющая Y приняла значение y ₁ и двумерная случайная величина (Х, Y) задана таблицей:

X Y	x 1	x 2	x 3
y 1	0,10	0,30	0,20
y 2	0,06	0,18	0,16

Решение. Используя формулу

,

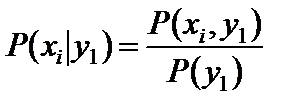где P (y ₁) = 0,10 + 0,30 + 0,20 = 0,60, находим:

;

;

.

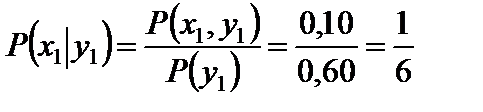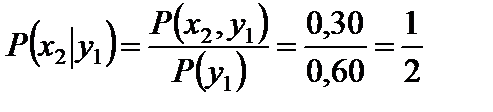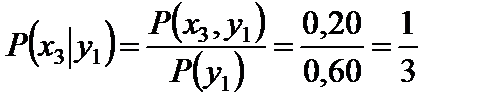Для проверки вычислений просуммируем найденные вероятности:

.

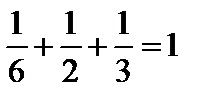Искомый условный закон распределения X может быть записан в виде таблицы

X	x 1	x 2	x 3

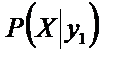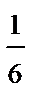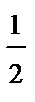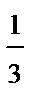Аналогично найдем условный закон распределения Y, который приведен в виде следующей таблицы:

Y	y 1	y 2

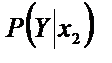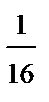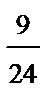Проверка: .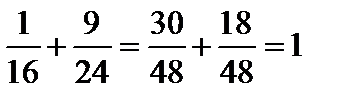

3.2. Числовые характеристики системы
двух случайных величин

Среди числовых характеристик двумерной случайной величины важнейшими являются условное математическое ожидание и ковариация.

Условным математическим ожиданием дискретной случайной величины Y при X = x называется сумма произведений возможных значений Y на их условные вероятности:

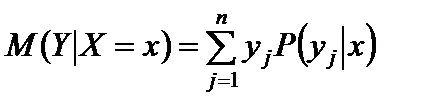. (80)

Условное математическое ожидание дискретной случайной величины X при Y = y рассчитывается по следующей формуле:

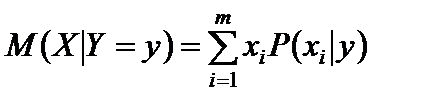. (81)

Ковариацией или корреляционным моментом случайных величин X и Y называется математическое ожидание произведения отклонений этих величин от их математических ожиданий:

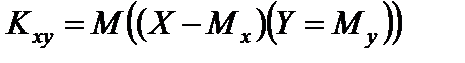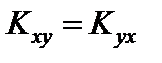; . (82)

Коэффициентом корреляции r_xy случайных величин X и Y называется отношение ковариации к произведению средних квадратичных отклонений этих величин:

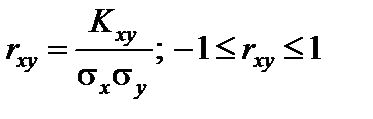. (83)

Корреляционные моменты и дисперсии можно представить в виде корреляционной матрицы:

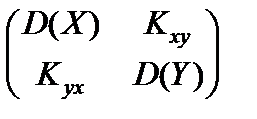. (84)

Пример 3.3. Найти условное математическое ожидание составляющей Y при Y = x ₁ = 1, если дискретная двумерная случайная величина (Y, Х) задана следующей таблицей:

X Y	x 1 = 1	x 2 = 3	x 3 = 4	x 4 = 8
y 1 = 3	0,15	0,06	0,25	0,04
y 2 = 6	0,30	0,10	0,03	0,07

Решение. Найдем P (x ₁) = 0,15 + 0,30 = 0,45.

;

.

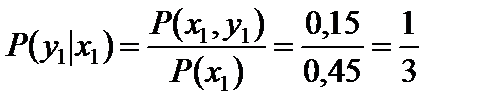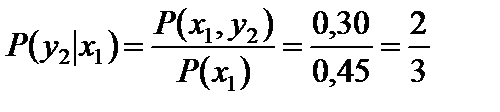Условное математическое ожидание равно:

.

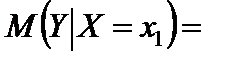
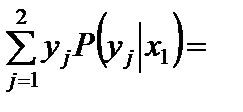
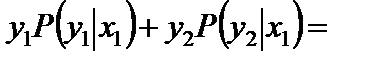
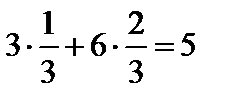Пример 3.4. Закон распределения двумерной случайной величины (X, Y) задан в виде следующей таблицы:

X Y
	0,10	0,05	0,12
	0,20	0,14	0,08
	0,15	0,11	0,05

Найти следующее:

а) одномерные законы распределения компонент X и Y;

б) корреляционный момент;

в) корреляционную матрицу;

г) коэффициент корреляции.

Решение.

1. Составим одномерные законы распределения X и Y.

Находим вероятности возможных значений X:

;

;

.

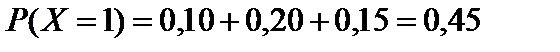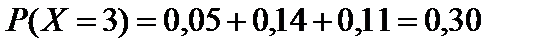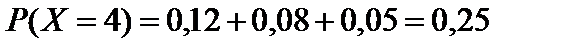Проверка: .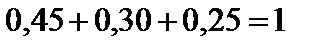

Аналогично находим вероятности возможных значений Y, сложив вероятности по строкам:

;

;

.

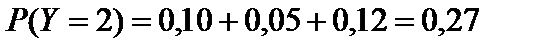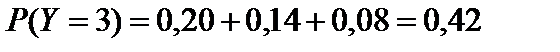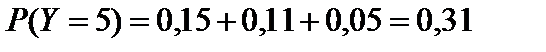Проверка: .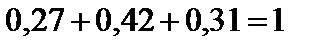

X
P	0,45	0,30	0,25

Y
P	0,27	0,42	0,31

.

.

.

.

.

.

; .

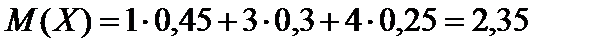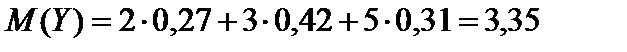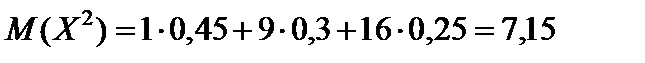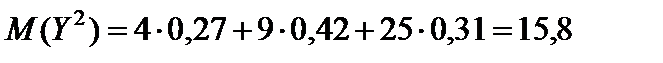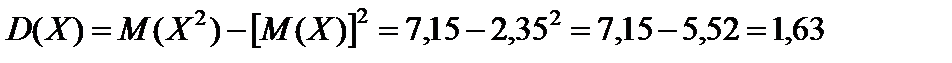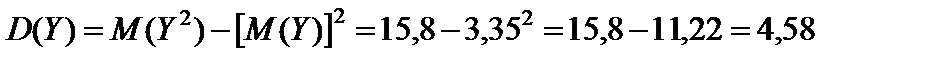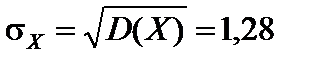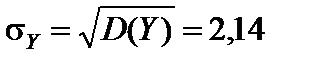2. Находим корреляционный момент по следующей формуле:

.

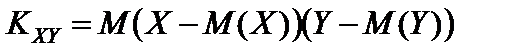Составляем закон распределения двумерной случайной величины (Y, Х) в виде таблицы:

X – M (X) Y – M (Y)	– 1,35	0,65	1,65
– 1,35	0,10	0,05	0,12
– 0,35	0,20	0,14	0,08
1,65	0,15	0,11	0,05

K_XY = –1,35(–1,35 · 0,1 + 0,65 · 0,05 + 1,65 · 0,12) – 0,35(–1,35 · 0,2 +
+ 0,65 · 0,14 + 1,65 · 0,08) + 1,65 · (–1,35 · 0,15 + 0,65 · 0,11 + 1,65 · 0,05) =
= –1,35 · (–0,135 + 0,0325 + 0,138) – 0,35(–0,27 + 0,091 + 0,132) +
+ 1,65(–0,2025 + 0,0715 + 0,0825) = –0,128 + 0,0165 – 0,08 = 0,19.

3. Записывает корреляционную матрицу:

.

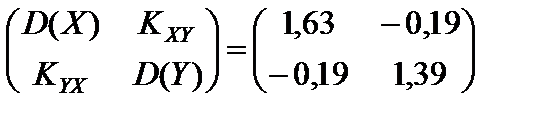4. Находим коэффициент корреляции по формуле (83):

.

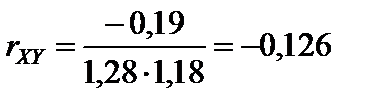Так как 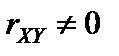, величины X и Y являются зависимыми.