Решение с помощью ППП Excel

1. Встроенная статистическая функция ЛИНЕЙН определяет пара­метры линейной регрессии y=a+b×x. Порядок вычисления сле­дующий:

1. введите исходные данные или откройте существующий файл, содержащий анализируемые данные;

2. выделите область пустых ячеек 5х2 (5 строк, 2 столбца) для вы­вода результатов регрессионной статистики или область 1х2 - для получения только оценок коэффициентов регрессии;

3. активизируйте Мастер функций любым из способов:

а) в главном меню выберите Вставка/Функция;

б) на панели инструментов Стандартная щелкните по кнопке

Вставка/Функция;

4. окне Категория (рис. 1.1) выберите Статистические, в окне- ЛИНЕЙН. Щелкните по кнопке ОК;

5. заполните аргументы функции (рис. 1.2):

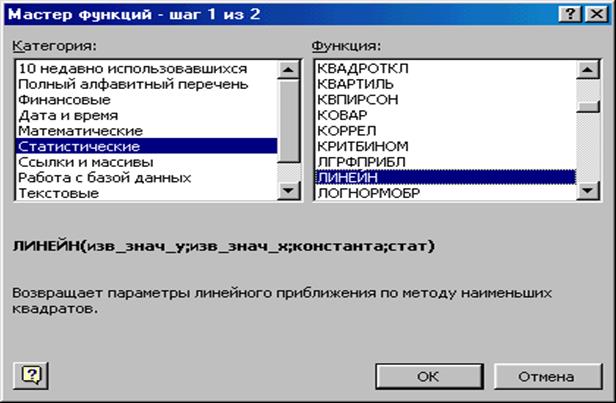Рис. 1.1. Диалоговое окно «Мастер функций»

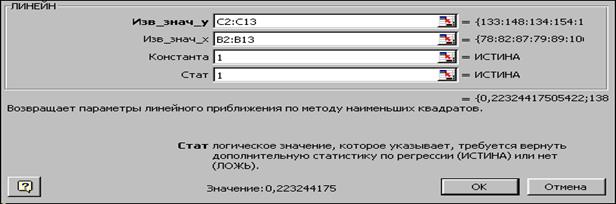Известные_значения_у - диапазон, содержащий данные резуль­тативного признака;

Рис. 1.2. Диалоговое окно ввода аргументов функции ЛИНЕЙН

Известные_значения_х - диапазон, содержащий данные факто­ров независимого признака;

Константа - логическое значение, которое указывает на нали­чие или на отсутствие свободного члена в уравнении; если Константа = 1, то свободный член рассчитывается обычным обра­зом, если Константа = 0, то свободный член равен 0;

Статистика - логическое значение, которое указывает, выво­дить дополнительную информацию по регрессионному анализу или нет. Если Статистика = 1, то дополнительная информация выводится, если Статистика = 0, то выводятся только оценки параметров уравнения.

Щелкните по кнопке ОК;

6. в левой верхней ячейке выделенной области появится пер­вый элемент итоговой таблицы. Чтобы раскрыть всю таблицу, наж­мите на клавишу <F2>, а затем - на комбинацию клавиш <CTRL>+<SHIFT>+<ENTER>.

Дополнительная регрессионная статистика будет выводиться в порядке, указанном в следующей схеме:

Значение коэффициента b	Значение коэффициента а
Среднеквадратическое отклонение b	Среднеквадратическое отклонение а
Коэффициент детерминации R2	Среднеквадратическое отклонение у
F-статистика	Число степеней свободы
Регрессионная сумма квадратов	Остаточная сумма квадратов

Для вычисления параметров экспоненциальной кривой y=α×β^x в MS Excel применяется встроенная статистическая функция ЛГРФПРИБЛ. Порядок вычисления аналогичен примене­нию функции ЛИНЕЙН.

Для данных из примера 2 результат вычисления функции ЛИНЕЙН представлен на рис. 1.3, функции ЛГРФПРИБЛ - на рис. 1.4.

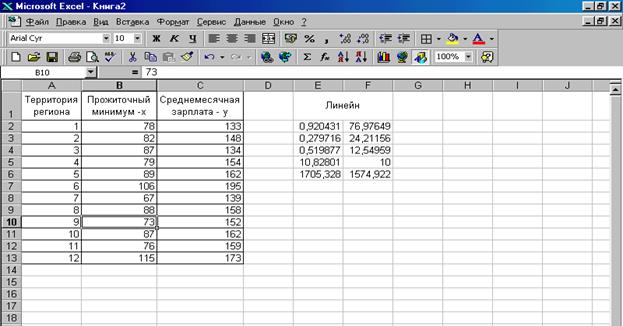Рис. 1.3. Результат вычисления функции ЛИНЕЙН

Рис. 1.4. Результат вычисления функции ЛГФПРИБЛ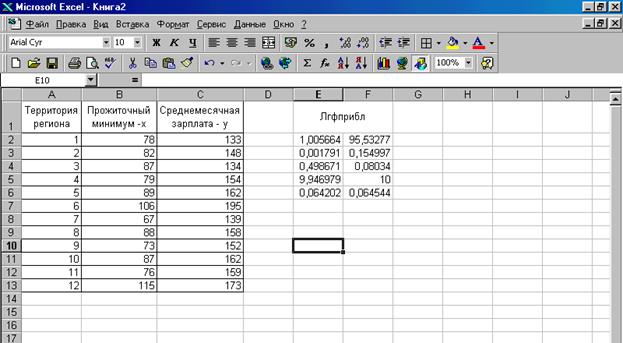

2.С помощью инструмента анализа данных Регрессия, помимо ре­зультатов регрессионной статистики, дисперсионного анализа и до­верительных интервалов, можно получить остатки и графики подбо­ра линии регрессии, остатков и нормальной вероятности. Порядок действий следующий:

1)

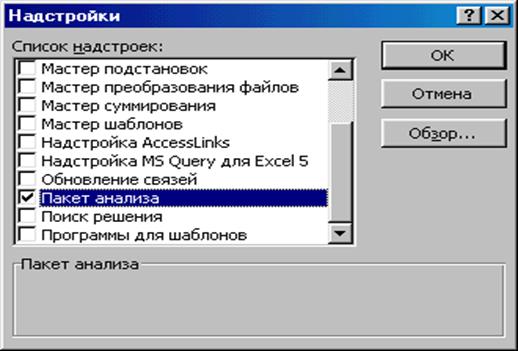проверьте доступ к пакету анализа. В главном меню последо­вательно выберите Сервис /Надстройки. Установите флажок Пакет анализа (рис. 1.5);

Рис. 1.5. Подключение надстройки Пакет анализа.

2) в главном меню выберите Сервис/Анализ данных/Регрессия. Щелкните по кнопке ОК;

3) заполните диалоговое окно ввода данных и параметров выво­да (рис. 1.6):

Входной интервал Y - диапазон, содержащий данные результа­тивного признака;

Входной интервал Х - диапазон, содержащий данные факторов независимого признака;

Метки - флажок, который указывает, содержит ли первая строка названия столбцов или нет;

Константа - ноль - флажок, указывающий на наличие или от­сутствие свободного члена в уравнении;

Выходной интервал - достаточно указать левую верхнюю ячейку будущего диапазона;

Новый рабочий лист - можно задать произвольное имя нового листа.

Если необходимо получить информацию и графики остатков, установите соответствующие флажки в диалоговом окне. Щелкните по кнопке OK.

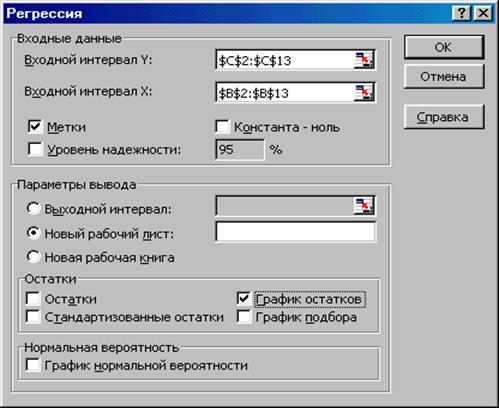Рис. 1.6. Диалоговое окно ввода параметров инструмента Регрессия.

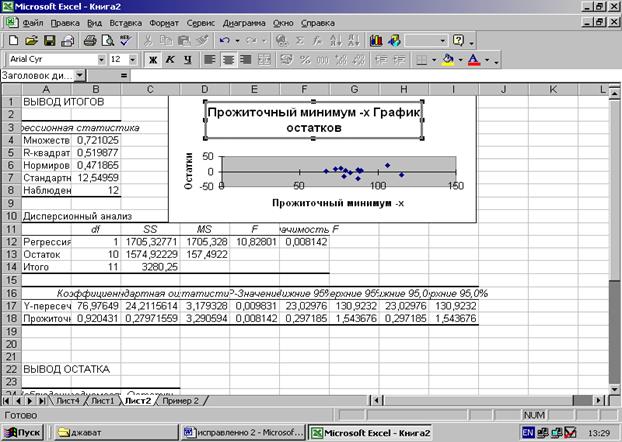
Рис. 1.7. Результат применения инструмента Регрессия.

В задачах 1-8 выполните:

Задание

1. Постройте поле корреляции и сформулируйте гипотезу о форме связи

2. Рассчитайте параметры уравнений линейной, степенной, экспоненциальной, полулогарифмической, обратной, гиперболической регрессии.

3. Оцените тесноту связи с помощью показателей корреляции и детерминации

4. "Дайте с помощью среднего (общего) коэффициента эластичности сравнительную оценку силы связи фактора с результатом.

5. Оцените с помощью средней ошибки аппроксимации качество уравнений.

6. Оцените с помощью F-критерия Фишера статистическую надеж­ность результатов регрессионного моделирования. По значениям характеристик, рассчитанных в пп. 4, 5 и данном пункте, выберите лучшее уравнение регрессии и дайте его обоснование.

7. Рассчитайте прогнозное значение результата, если прогнозное значение фактора увеличится на 10% от его среднего уровня. Опре­делите доверительный интервал прогноза для уровня значимости =0,05.

8. Оцените полученные результаты, выводы оформите в аналитиче­ской записке.

Задача 1.По территориям Центрального района известны данные за 1995 г. (табл. 1.1).

Таблица 1.1

Район	Доля денежных доходов, направленных на прирост сбережений во вкладах. займах. сертификатах и на покупку валюты, в общей сумме среднедушевого денежного дохода, %, у	Среднемесячная на­численная заработная плата, тыс. руб., х
Брянская обл.	6,9
Владимирская обл.	8,7
Ивановская обл.	6,4
Калужская обл.	8,4
Костромская обл.	6,1
Орловская обл.	9,4
Рязанская обл.	11,0
Смоленская обл.	6,4
Тверская обл.	9,3
Тульская обл.	8,2
Ярославская обл.	8,6

Задача 2.

По территориям Центрального района известны данные за 1995 г. (табл. 1.2).

Таблица 1.2

Район	Средний размер назначенных ежемесячных пенсий, тыс. руб., у	Прожиточный минимум в среднем на одного пенсионера в месяц, тыс. руб., х
Брянская обл.
Владимирская обл.
Ивановская обл.
Калужская обл.
Костромская обл.
г. Москва
Московская обл.
Орловская обл.
Рязанская обл.
Смоленская обл.
Тверская обл.
Тульская обл.
Ярославская обл.

Задача 3.

По территориям Центрального и Волго-Вятского районов из­вестны данные за ноябрь 1997 г. (табл. 1.3).

Таблица 1.3

Район	Средняя заработная плата и выплаты социального характера, тыс. руб., у	Прожиточный минимум в среднем на душу населения, тыс. руб., х
Центральный
Брянская обл.
Владимирская обл.
Ивановская обл.
Калужская обл.
Костромская обл.
Орловская обл.
Рязанская обл.
Смоленская обл.
Тверская обл.
Тульская обл.
Ярославская обл.
Волго-Вятский район
Респ. Марий Эл
Респ. Мордовия
Чувашская Респ.
Кировская обл.
Нижегородская обл.

Задача 4.

По территориям Волго-Вятского, Центрально-Черноземного и Поволжского районов известны данные за ноябрь 1997 г. (табл. 1.19).

Таблица 1.4

Район	Потребительские расходы в расчете на душу населения, тыс. руб., у	Средняя заработная плата и выплаты социального харак­тера, тыс. руб., х
Волго-Вятский
Респ. Марий Эл
Респ. Мордовия
Чувашская Респ.
Кировская обл.
Нижегородская обл. -
Центрально-Черноземный
Белгородская обл.
Воронежская обл.
Курская обл.
Липецкая обл.
Тамбовская обл.
Поволжский
Респ. Калмыкия
Респ. Татарстан
Астраханская обл.
Волгоградская обл.
Пензенская обл.
Саратовская обл.
Ульяновская обл.

Задача 5.

По территориям Северного, Северо-западного и Центрального районов известны данные за ноябрь 1997 г. (табл. 1.5).

Таблица 1.5

Район	Потребительские расходы на душу населения, тыс. руб., у	Денежные доходы на душу населения, тыс. руб., х
Северный
Респ. Карелия
Респ. Коми
Архангельская обл.
Вологодски обл.
Мурманская обл.
Сеаеро-Западный
Ленинградская обл.
Новгородская обл.
Псковская обл.
Центральный
Брянская обл.
Владимирская обл.
Ивановская обл.
Калужская обл.
Костромская обл.
Московская обл.
Орловская обл.
Рязанская обл.
Смоленская обл.
Тверская обл.
Тульская обл.
Ярославская обл.

Задача 6.

По территориям Восточно-Сибирского и Дальневосточного районов известны данные за ноябрь 1997 г. (табл. 1.6).

Таблица 1.6

Район	Потребительские расходы на душу населения, тыс. руб., у	Денежные дохо­ды на душу населения, тыс. руб., х
Восточно-Сибирский
"Респ. Бурятия
Рссп. Тыва
Респ. Хакасия
Красноярский край
Иркутская обл.
Усть-Ордынский Бурятский авт. округ.
Читинская обл.
Респ. Саха (Якутия)
Еврейская авт. обл.
Чукотский авт. округ
Приморский край
Хабаровский край
Амурская обл.
Камчатская обл.
Магаданская обл.
Сахалинская обл.

Задача 7

По территориям Уральского и Западно-Сибирского районов из­вестны данные за ноябрь 1997 г. (табл. 1.7).

Таблица 1.7

Район	Потребительские расходы на душу населения, тыс. руб., у	Денежные доходы на душу населения, тыс. руб., х
Уральский
Респ. Башкортостан
Удмуртская Респ.
Курганская обл.
Оренбургская обл.
Пермская обл.
Свердловская обл.
Челябинская обл.
Западносибирский район
Респ. Алтай
Алтайский край
Кемеровская обл.
Новосибирская обл.
Омская обл.
Томская обл.
Тюменская обл.

Задача 8.

По территориям Уральского и Западно-Сибирского районов из­вестны данные за ноябрь 1997 г. (табл. 1.8).

Таблица 1.8

Район	Потребительские расходы на душу населения, тыс. руб., у	Средняя заработная плата и выплаты со­циального характера, тыс. руб., х
Уральский
Респ. Башкортостан
Удмуртская Респ.
Курганская обл.
Оренбургская обл.
Пермская обл.
Свердловская обл.
Челябинская обл.
Западно-Сибирский
Респ. Алтай
Алтайский край
Кемеровская обл.
Новосибирская обл.
Омская обл.
Томская обл.
Тюменская обл.

Задача 9.

По 20 регионам страны изучается зависимость уровня безрабо­тицы у (%) от индекса потребительских цен x (% к предыдущему году). Информация о логарифмах исходных показателей представ­лена в табл. 1.9.

Таблица 1.9

Показатель	In x;	In у
Среднее значение	0,6	1,0
Среднее квадратическое отклонение	0,4	0,2

Известно также, что коэффициент корреляции между логариф­мами исходных показателей составил r_{lnx lny} = 0,8.

Задание

1. Постройте уравнение регрессии зависимости уровня безработицы от индекса потребительских цен в степенной форме.

2. Дайте интерпретацию коэффициента эластичности данной модели регрессии.

3. Определите значение коэффициента детерминации и поясните его смысл.

Задача 10.

Изучается зависимость материалоемкости продукции от размера предприятия по 10 однородным заводам (табл. 1.10).

Таблица 1.10

Показатель	Материалоемкость продукции по заводам
Потребле­но мате­риалов на единицу продукции, кг					3,7	3,6	3,5			3,5
Выпуск продукции, тыс. ед.

Задание

1. Найдите параметры уравнения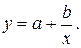

2. Оцените тесноту связи с помощью индекса корреляции.

3. Охарактеризуйте эластичность изменения материалоемкости продукции.

4. Сделайте вывод о значимости уравнения регрессии.

Оцените полученные результаты, выводы оформите в аналитиче­ской записке.