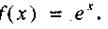2015-05-20
186
Рассмотрим конкретные разложения по формуле (38) некоторых важнейших элементарных функций.
Разложение функции
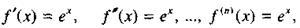Поскольку
 |
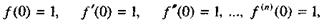формула (38) для функции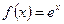 
принимает вид
 |
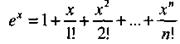(39)
 |
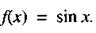Разложение функции
 |
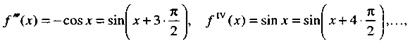Так как
 |
 |
 |
 |
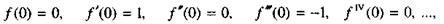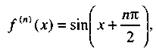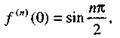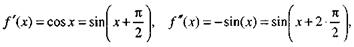то
 |
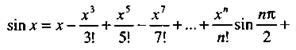(40)
Разложение функции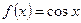 
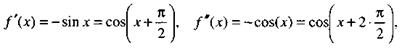Поскольку
 |
 |
 |
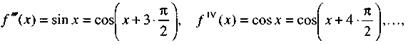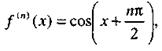
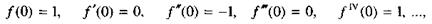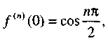то
 |
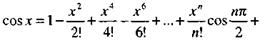(41)
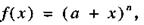Разложение функции
где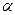 
- действительное число, п - натуральное число. Поскольку k -я производная данной функции
 |
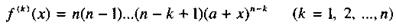при х = 0 принимает значение
 |
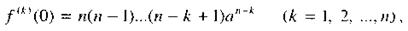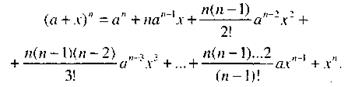то
(42)
Это равенство называется формулой бинома Ньютона.
