Метод дихотомии

Метод дихотомии называют также методом половинного деления. Суть метода состоит в следующем. Определяют середину отрезка [a,b], на котором находится корень 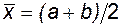, и вычисляют функцию 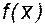. Далее делают выбор, какую из двух частей отрезка взять за уточнение корня. Если на интервале 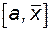функция f(x) меняет знак, то точку b перемещают в точку 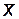. Если на интервале 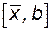функция f(x) меняет знак, то точку а перемещают в точку 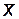. Далее процесс повторяется до тех пор, пока значение функции f(x) не станет меньше по абсолютной величине заданной погрешности 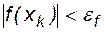. Графическая интерпретация метода дихотомии приведена на рис.2.2.

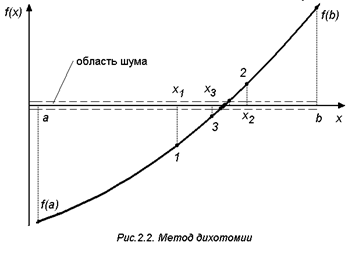Следует заметить, что функция вычисляется с погрешностью 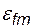, определяемой методом вычислений и возможностями ЭВМ. Интервал 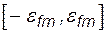называется областью шума. Если задать 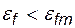, мы не сможем получить точность, определяемую 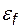. Вторым критерием окончания поиска корня методом дихотомии является неравенство (2.2). Заданные погрешности функции и аргумента должны быть согласованы по величине. По методу дихотомии за каждую итерацию интервал уменьшается в два раза. За k итераций он уменьшается в 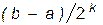раз.