Математическим ожиданием дискретной случайной величины называют сумму произведений всех ее возможных значений на их вероятности.
Пусть случайная величина X может принимать только значения xl, x2,..., хп, вероятности которых соответственно равны р1, р2,..., рп. Тогда математическое ожидание М(X) случайной величины X определяется равенством
М (X) = х1р1 + х2ра +... + хпрп.
Если дискретная случайная величина X принимает счетное множество возможных значений, то 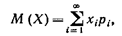 , причем математическое ожидание существует, если ряд в правой части равенства сходится абсолютно.
, причем математическое ожидание существует, если ряд в правой части равенства сходится абсолютно.
Замечание. Из определения следует, что математическое ожидание дискретной случайной величины есть неслучайная (постоянная) величина. Рекомендуем запомнить, что математическое ожидание непрерывной случайной величины также есть постоянная величина.
Пример 1. Найти математическое ожидание случайной величины X, зная закон ее распределения: 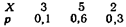
Решение. Искомое математическое ожидание равно сумме произведений всех возможных значений случайной величины на их вероятности:
|
|
|
М (Х) = 3*0,1+5*0,6 + 2*0,3 = 3,9.
Пример 2. Найти математическое ожидание числа появлений события А в одном испытании, если вероятность события А равна р.
Решение. Случайная величина X— число появлений события А в одном испытании — может принимать только два значения: х1=1 (событие А наступило) с вероятностью р и х2 = 0 (событие А не наступило) с вероятностью q = 1 – р. Искомое математическое ожидание
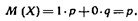
 2015-05-12
2015-05-12 1018
1018
