1. Формула Ньютона–Лейбница:
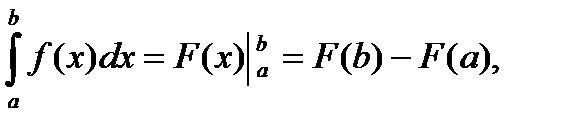
где F′ (x) = f (x).
2. Замена переменной:
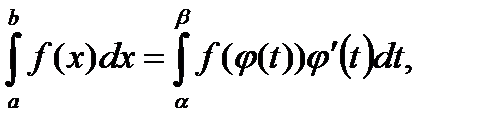
где x = 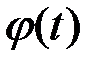 – функция, непрерывная вместе с
– функция, непрерывная вместе с 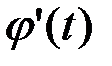 на отрезке
на отрезке 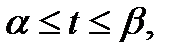
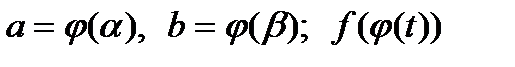 – функция, непрерывная на отрезке
– функция, непрерывная на отрезке 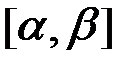 .
.
3. Интегрирование по частям: 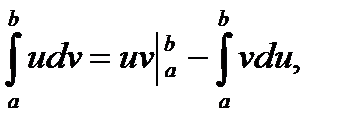
где u = u(x), v = v(x) – дифференцируемые на [a, b] функции.
4. Если f(x) – нечетная функция, то 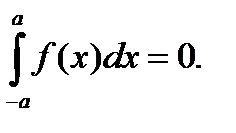
5. Если f(x) – четная функция, то 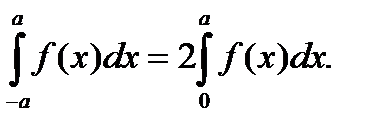
Примеры.
1) 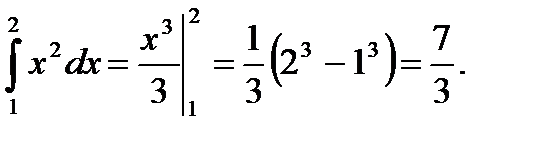
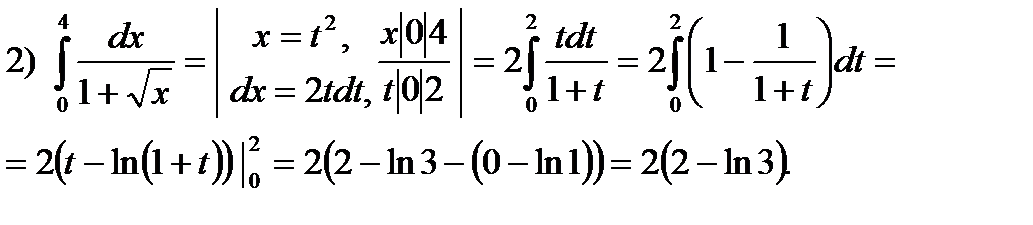
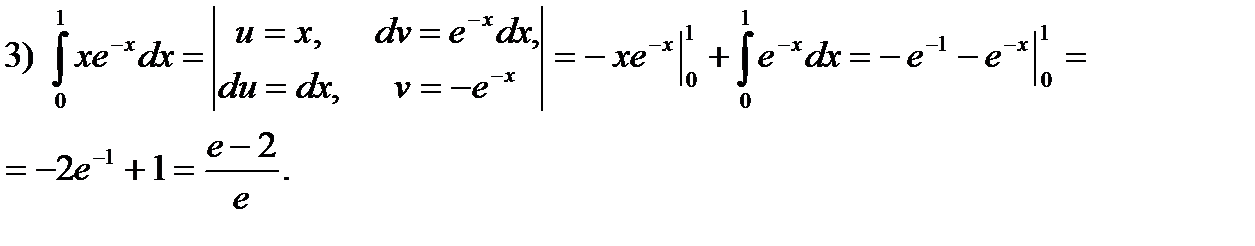
2.58. Вычислить интегралы:
1) 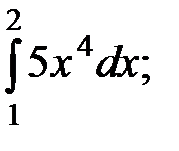 2)
2) 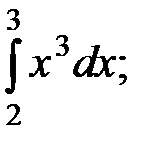 3)
3) 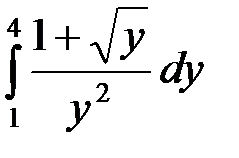 ; 4)
; 4) 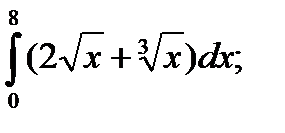
5) 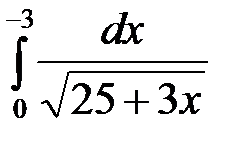 ; 6)
; 6) 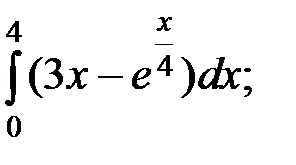 7)
7) 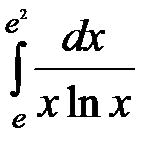 ; 8)
; 8) 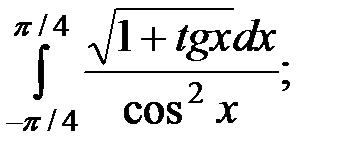
9) 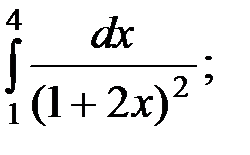 10)
10) 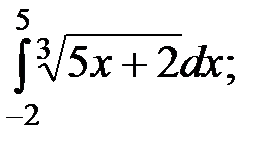 11)
11) 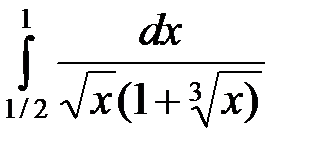 ; 12)
; 12) 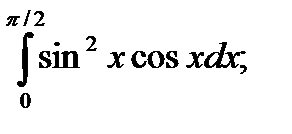
13) 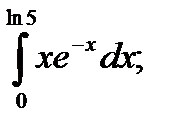 14)
14) 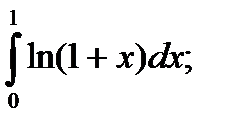 15)
15) 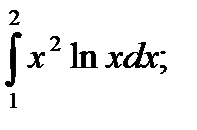 16)
16) 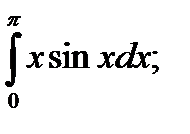
17) 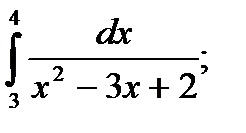 18)
18) 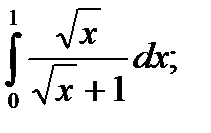 19)
19) 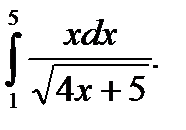
2.6.2. Геометрические приложения
определенного интеграла
 2015-05-12
2015-05-12 371
371








