2015-05-12
1558
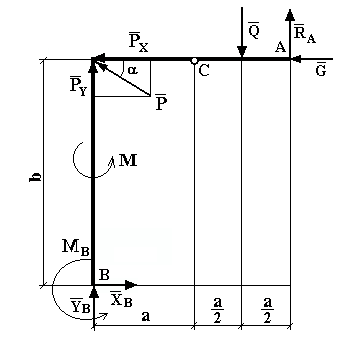
Рис. 7
Для полученной плоской произвольной системы сил можем составить три уравнения равновесия, а число неизвестных - четыре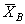 
, 
, 
, 
.
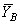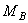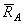Чтобы задача стала статически определимой, конструкцию расчленяем по внутренней связи - шарниру С и получаем еще две расчетные схемы (рис. 8, рис. 9).
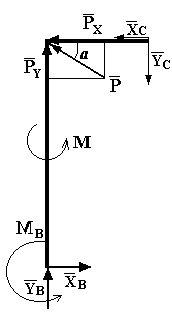
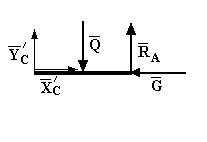
Рис. 8 Рис. 9
, 
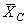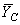заменяют действие тела АС на тело СВ, которое передается через шарнир С. Тело СВ передает свое действие на тело АС через тот же шарнир С, поэтому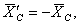 
; 
, 
.
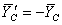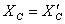Для трех расчетных схем в сумме можем составить девять уравнений равновесия, а число неизвестных – шесть 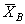, , 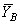, , 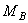, , 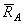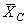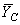то есть задача стала статически определима. Для решения задачи используем рис. 8, 9, а рис. 7 оставим для проверки.
Тело ВС (рис. 8)
1) 
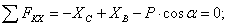
2) 
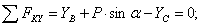
3) 
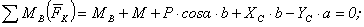
Тело СА (рис. 9)
4) 
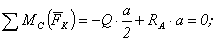
5) 
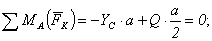
6) 
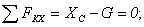
Решаем систему шести уравнений с шестью неизвестными.
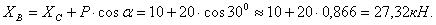
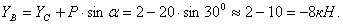
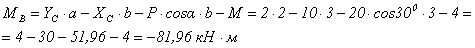
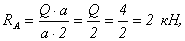
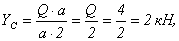
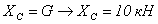
Проверка:
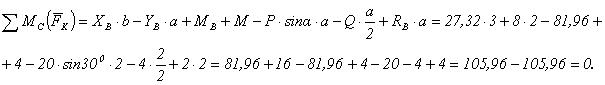
Реакции внешних опор в точках А и В найдены верно. Давление в шарнире С вычисляем по формуле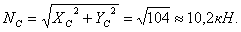 
Ответ: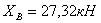 
, 
, 
, 
, 
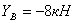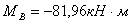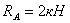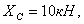
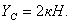
Минусы означают, что направления 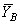и 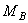надо изменить на противоположные.
|
|
|
Пример 5. Конструкция состоит из двух частей. Установить, при каком способе соединения частей конструкции модуль реакции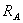 
наименьший, и для этого варианта соединения определить реакции опор, а также соединения С.
Дано: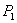 
= 9 кН; 
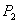= 12 кН; 
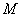= 26 кНм; 
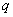= 4 кН/м.
Схема конструкции представлена на рис.10.
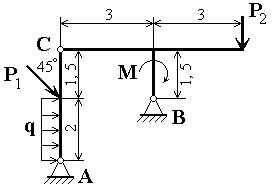
Рис.10
Решение:
1) Определение реакции опоры А при шарнирном соединении в точке С.
Рассмотрим систему уравновешивающихся сил, приложенных ко всей конструкции (рис.11). Составим уравнение моментов сил относительно точки B.
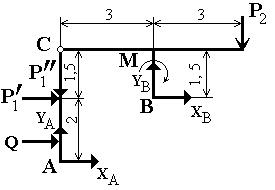
Рис.1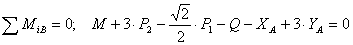1
(1)
где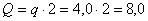 
кН.
После подстановки данных и вычислений уравнение (26) получает вид:
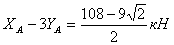(2)
Второе уравнение с неизвестным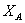и 
и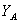 
получим, рассмотрев систему уравновешивающихся сил, приложенных к части конструкции, расположенной левее шарнира С (рис. 12):
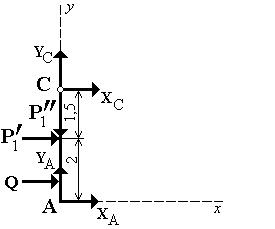
Рис. 12
.
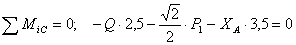Отсюда находим, что
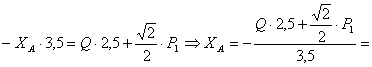
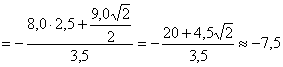кН.
Подставив найденное значение 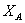в уравнение (2) найдем значение :
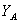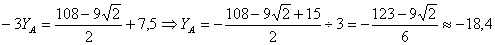кН.
Модуль реакции опоры А при шарнирном соединении в точке С равен:
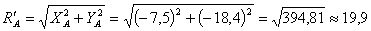кН.
2) Расчетная схема при соединении частей конструкции в точке С скользящей заделкой, показанной на рис. 13.
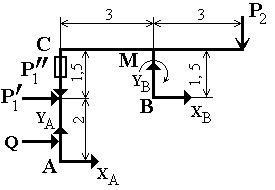
Рис. 13
Системы сил, показанные на рис. 12 и 13, ничем друг от друга не отличаются. Поэтому уравнение (2) остается в силе. Для получения второго уравнения рассмотрим систему уравновешивающихся сил, приложенных к части конструкции, расположенной левее скользящей заделки С (рис. 14).
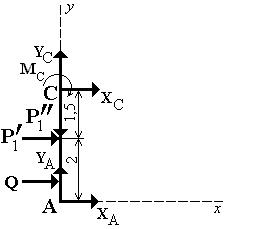
Рис. 14
Составим уравнение равновесия:
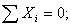
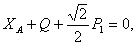
откуда
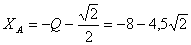
и из уравнения (2) находим:
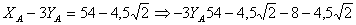
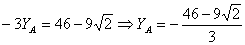
Следовательно, модуль реакции при скользящей заделке в шарнире С равен:
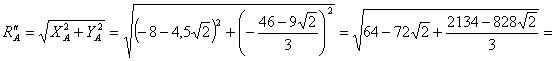
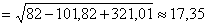кН.
Итак, при соединении в точке С скользящей заделкой модуль реакции опоры А меньше, чем при шарнирном соединении (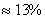
).
|
|
|
Найдем составляющие реакции опоры В и скользящей заделки.
Для левой от С части
,
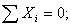
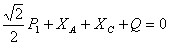откуда
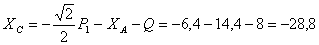кН.
Составляющие реакции опоры В и момент в скользящей заделке найдем из уравнений равновесия, составленных для правой от С части конструкции.
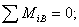
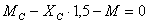
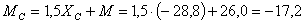кНм
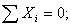
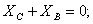
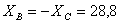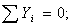
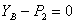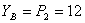кН
; 
кН
Ответ: Результаты расчета приведены в таблице.
| Силы, кН | Момент, кНм | ||||||
| XA | YA | RA | XC | XB | YB | MC | |
| Для схемы на рис.11 | -7,5 | -18,4 | 19,9 | - | - | - | - |
| Для схемы на рис.13 | -14,36 | -11,09 | 17,35 | -28,8 | 28,8 | 12,0 | -17,2 |
