Метод штрафных функций

Рассмотрим решение задачи условной оптимизации

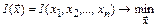(2.52)

при

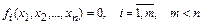(2.53)

метод штрафных функций заключается в безусловной минимизации обобщенной целевой функции

(2.54)

где 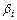, 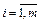– коэффициенты штрафа;

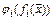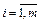, – штрафные функции.

В отличии от множителей Лагранжа коэффициенты штрафа задаются: 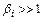. Обычно .

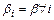Функции штрафа должны удовлетворять условию

,

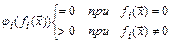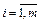
При решении задач оптимизации широко используется квадратичные и модульные штрафы:

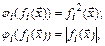
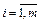
С помощью штрафной функции исходная задача (2.52), (2.23) условной минимизации преобразуется в последовательность задач безусловной минимизации функции (2.54). Эта задача решается численными методами, но условия оптимальности классического анализа могут быть использованы и здесь:

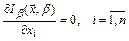
Решение этой системы даёт , .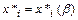

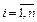В общем случае невозможно аналитически определить положение минимума функции 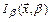, рассматривая её как обычную функцию от от β. Для его определения необходимо обратится к численным методам.

При 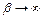решение задачи безусловной минимизации стремится к решению 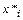задачи нелинейного программирования:

,

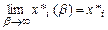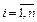
Наряду с этими многочисленными исследованиями доказано, что обязательным следствием неограниченного увеличения штрафного параметра β является плохая обусловленность подзадач безусловной минимизации, проявляющаяся в сильной деформации соответствующих поверхностей уровня.

Поэтому для того, чтобы можно было применить настоящий метод на практике, необходимо построить вычислительный алгоритм, использующий теоретическое свойство сходимости последовательности оптимальных решений подзадач безусловной оптимизации к оптимальному решению 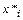, , 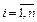задачи с ограничениями. Теоретически здесь не возникает трудностей. Необходимо выбрать начальное значение β = β⁽⁰⁾, что бы сформировать функцию 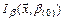, которая минимизируется без ограничений численными методами. Найдя минимум функции 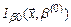, необходимо увеличить значение β. Это можно сделать просто, если найти 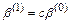, где константа с>1, однако выбор с произволен, удачным могут быть различные значения С в зависимости от свойств функции 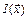и ограничений 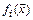. Затем необходимо минимизировать функцию 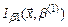, снова используя численный метод. Таким образом, будет заработана итерационная процедура. На каждом шаге минимизируется функция 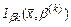, минимум которой находится в точке 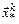. Важно, что её можно использовать в дальнейшем в качестве начальной точки в итерационной процедуре минимизации функции 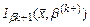, где β^(к+1) = с β^(к)

Теперь ясно, что последовательность β^(к) возрастает и стремиться к бесконечности, следовательно, последовательность точек минимумов 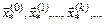безусловной минимизации будет сходиться к решению исходной задачи с ограничениями .

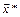Выбор начального значения β⁽⁰⁾ может оказаться важным с точки зрения сокращения числа итераций при минимизации функции 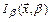. Если сначала β⁽⁰⁾ выбрано очень малым, для того чтобы функция 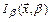мало отличалась от функции 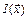, то метод будет сходится очень быстро. Однако такой выбор может привести к серьёзным осложнениям при вычислениях. Для малых β функция 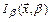будет быстро меняться в окрестности минимума, что может вызвать затруднения при использовании градиентных методов. Слишком же большое значение β может привести к тому, что штрафная функция

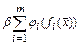
в выражении (2.24) станет доминирующей. Поэтому разумный выбор начальной точки β⁽⁰⁾ очень важен. Для многих задач разумным значением для начальной точки является значение β⁽⁰⁾ =1.

Для уменьшения влияния произвола в выборе коэффициента штрафа применяют метод последовательной безусловной минимизации (МПБМ) Мак-Кормика и Фиакко, состоящий обобщенной функции Iβ ﴾x,β﴿ с увеличивающимся штрафом:

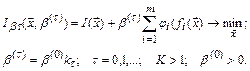
при этом оптимальное значение 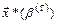используют как начальную точку на 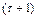-ом цикле минимизации. Обычно берут k = 4-2, β₀ = 1 и заканчивают поиск, когда решение 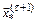мало отличается от предыдущего решения 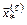на предыдущем цикле.

Метод штрафных функций приводит задачу условной оптимизации той же размерности, что и исходная, в отличие от метода Лагранжа. Метод легко алгоритмизируется для ЭВМ, но требует опыта выбора коэффициентов штрафа и даёт отлично невысокую точность; находит наибольшие применение при численном решении задач на ЭВМ.